Hans Walser, [20150127]
Schnittpunkt mit Dreiecken
1 Worum geht es?
Es wird ein Schnittpunkt mit Dreiecken erarbeitet. Die Schlźsselidee ist eine zentrische Streckung.
2 Dreiecke ansetzen
Wir
beginnen mit einem beliebigen Dreieck 
(Abb. 1)
und einer beliebigen reellen Zahl 
. Fźr die folgenden Figuren ist 
gewŠhlt
worden.
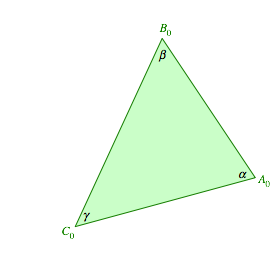
Abb. 1: Startdreieck
Nun
verŠndern wir eine Kopie des Dreieckes mit dem LŠngenfaktor 
und setzen
diese Kopie verdreht gemŠ§ Abbildung 2 an.
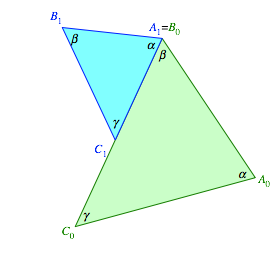
Abb. 2: Ansetzen des verŠnderten Dreiecks
Die
Abbildung vom Dreieck 
zum
Dreieck 
ist eine
Drehstreckung mit dem Drehwinkel 
und dem
Faktor 
.
Analog
fźgen wir ein weiteres Dreieck 
an (Abb.
3).
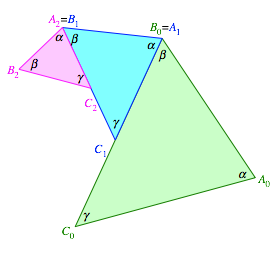
Abb. 3: NŠchstes Dreieck
3 Umkreise
In der Situation der Abbildung 3 ist es nun so, dass sich die drei Umkreise der drei Dreiecke in einem Punkt schneiden (Abb. 4).
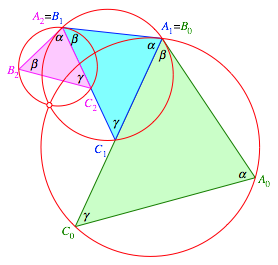
Abb. 4: Schnittpunkt der Umkreise
4 Beweis
Wir haben
bereits festgestellt, dass die Abbildung vom Dreieck 
zum
Dreieck 
eine
Drehstreckung mit dem Drehwinkel 
und dem
Faktor 
ist. Es
sei S das Zentrum (Fixpunkt) dieser
Drehstreckung. Dann ist der Winkel 
gleich dem
Drehwinkel, also 
. Somit liegt S
auf dem Ortsbogen fźr die Strecke 
und den
Winkel 
. Wegen 
ist das
der Umkreis des Dreieckes 
. Ebenso ist 
, und S
liegt daher auf dem Umkreis des Dreieckes 
. Somit ist S
der Schnittpunkt der beiden ersten Umkreise. Da sich das Dreieck 
durch
Iteration der zentrischen Streckung ergibt, liegt S entsprechend auch auf dem Umkreis dieses Dreieckes.
5 Iteration
Die Abbildung kann iteriert werden (Abb. 5). Wir erhalten eine eckige logarithmische Spirale mit dem Schnittpunkt der Umkreise als Zentrum.
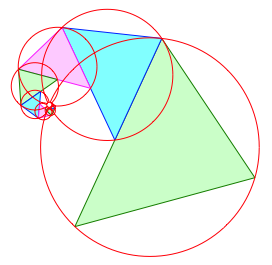
Abb. 5: Iteration
6 Sehnenvielecke
Der Sachverhalt kann auf Sehnenvielecke verallgemeinert werden. Die Abbildung 6 zeigt exemplarisch den Fall fźr ein Sehnenviereck.
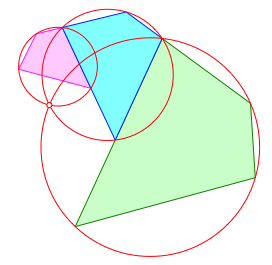
Abb. 6: Sehnenviereck
Beim Sehnenviereck gehen die Au§enrŠnder glatt durch. Das ist ein Sonderfall, die das Beispiel eines Sehnenfźnfeckes zeigt (Abb. 7).
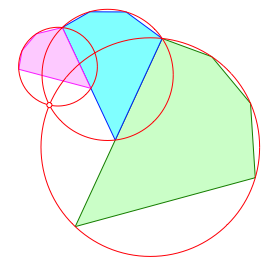
Abb. 7: Sehnenfźnfeck
Literatur
Walser, Hans (2006): 99 Points of Intersection. Examples – Pictures – Proofs. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America. ISBN 0-88385-553-4
Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0
Websites
Abgerufen 26.01.2015
http://www.walser-h-m.ch/hans/Schnittpunkte