Hans Walser, [20160810]

Schnittpunkt im Würfelbild

1 Worum geht es?

In einem normalaxonometrischen Würfelbild (orthografische Projektion, senkrechte Parallelprojektion) finden wir planimetrisch einen Schnittpunkt von drei Thaleskreisen.

Sonderfälle sind interessant.

2 Der Spielwürfel

Abb. 1: Spielwürfel

Ein guter Spielwürfel („gut“ nicht im Sinne der Wahrscheinlichkeit (Laplace-Würfel) sondern im Sinne des Rollverhaltens) ist die Schnittmenge eines geometrischen Würfels mit seiner Kantenmittenkugel. Die Kantenmittenkugel ist die Kugel, welche die Kantenmitten des Würfels berührt (Abb. 2, perspektivische Darstellung). Im Einheitswürfel hat die Kantenmittenkugel den Radius .

Abb. 2: Kantenmittenkugel

Die Abbildung 3 zeigt in perspektivischer Darstellung die Schnittmenge von Würfel und Kugel, also den geometrischen Spielwürfel. Die Ecken des geometrischen Würfels sind kugelförmig abgerundet.

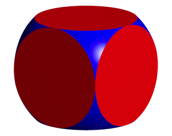
Abb. 3: Schnittmenge

Die Abbildung 4 zeigt in Normalaxonometrie den Würfel mit den Schnittkreisen auf der Oberfläche.

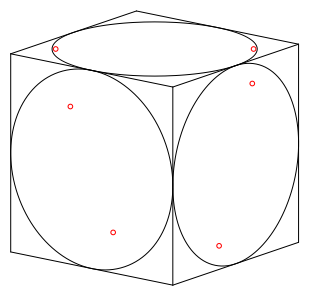
Abb. 4: Würfel in Normalaxonometrie

Rein planimetrisch gesehen erscheinen die drei sichtbaren Würfelseiten als Parallelogramme. Der Umriss der Gesamtfigur ist ein punktsymmetrisches Sechseck. Die Schnittkreise erscheinen als Ellipsen, welche die Kantenmitten der Parallelogramme berühren (Steinersche Inellipsen). In der Abbildung 4 sind auch die Brennpunkte dieser Ellipsen eingezeichnet.

Wir zeichnen nun die Thaleskreise über den drei Brennpunktstrecken (Abb. 5).

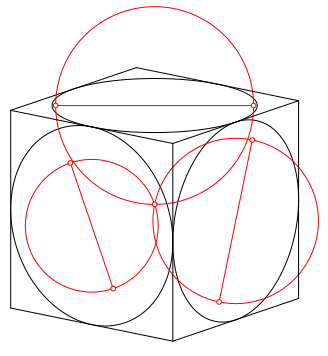
Abb. 5: Thaleskreise

Die drei Thaleskreise schneiden sich ein einem Punkt.

Abb. 6: Zentrum des Umrisssechseckes

Der Schnittpunkt ist zudem das Symmetriezentrum des Umrisssechseckes (Abb. 6). Das heißt, dass die drei nicht gezeichneten Thaleskreise für die Ellipsen auf der räumlichen Rückseite ebenfalls durch diesen Punkt gehen.

3 Beweis

Im Einheitswürfel hat die Kantenmittenkugel wie schon erwähnt den Radius . Die Schnittkreise mit den Würfelseiten haben den Radius . Die Ebenen dieser Schnittkreise haben vom Mittelpunkt den Abstand .

Wir zeichnen nun in Normalaxonometrie auf der Kugel mit dem Radius einen Kleinkreis mit dem Radius (Abb. 7). Seine Ebene hat vom Kugelzentrum den Abstand .

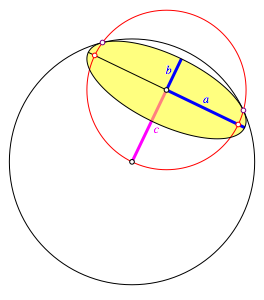
Abb. 7: Kleinkreis auf Kugel

Die Bildellipse des Kleinkreises hat die Halbachsen und , wobei der Neigungswinkel der Kleinkreisebene (im Raum) zur Projektionsebene ist.

Weiter sei c der planimetrische Abstand des Ellipsenmittelpunktes vom Zentrum des Kugelumrisses. Es ist . Also ist:

(1)

Somit ist c auch die halbe Brennpunktweite der Kleinkreisellipse. Der Thaleskreis über der Brennpunktstrecke verläuft daher durch das Zentrum des Kugelumrisses.

Interessant ist ein Zusatzresultat: Der Thaleskreis schneidet den Kugelumriss in den Berührungspunkten der Kleinkreisellipse mit dem Kugelumriss.

4 Sonderfälle

4.1 Frontalansicht

Die einfachste Figur ist oft die schwierigste. Stimmt die Figur der Abbildung 8?

Abb. 8: Frontalansicht

4.2 Ein Klassiker

Die Abbildung 9 zeigt einen Schulbuchklassiker im Karoraster. Welchen?

Abb. 9: Ein Klassiker

4.3 Isometrische Axonometrie

Die Abbildung 10 zeigt die Situation in isometrischer Darstellung.

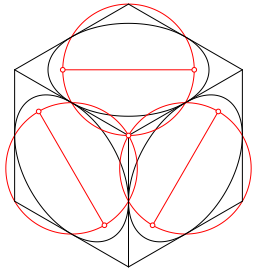
Abb. 10: Isometrische Darstellung

Aus der Abbildung 10 ergibt sich unmittelbar, dass die Brennpunkte der Steiner-Inellipse im 60°-Rhombus zusammen mit den stumpfen Ecken ein Quadrat bilden (Abb. 11).

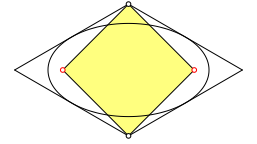
Abb. 11: Quadrat im 60°-Rhombus

Dies kann direkt durch Nachrechnen verifiziert werden.