Hans Walser, [20221112]

Schnittpunkt

Anregung: Maik Rentsch

1 Worum geht es?

Schnittpunkte von drei Kegelschnitten (Kreis, Ellipse, Hyperbel).

2 Konstruktionsgang

Wir beginnen mit einem beliebigen rechtwinkligen Dreieck, dessen eine Kathete auf einer horizontalen Standlinie liegt (Abb. 1).

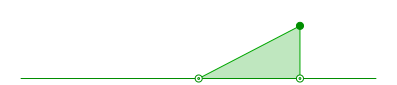
Abb. 1: Rechtwinkliges Dreieck

Nun zeichnen wir einen Kreis um die spitze Dreiecksecke auf der Standlinie durch die zweite spitze Ecke (Abb. 2). Der Radius dieses Kreises ist die Hypotenuse des rechtwinkligen Dreieckes. Die beiden Schnittpunkte dieses Kreises mit der Standlinie werden wir als gemeinsame Brennpunkte für die Ellipse und die Hyperbel verwenden.

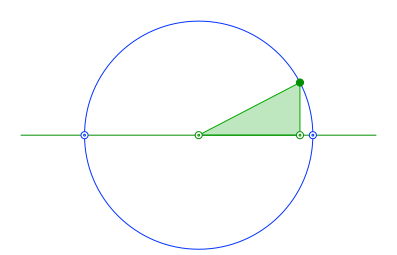
Abb. 2: Konstruktion der Brennpunkte

Wir zeichnen weiter einen kleinen Kreis um die Ecke mit dem rechten Winkel durch die zweite spitze Ecke (Abb. 3). Der Radius dieses Kreises ist die senkrecht zur Standlinie stehende Kathete des rechtwinkligen Dreieckes. Der äußere Schnittpunkt dieses Kreises mit der Standlinie ist ein Scheitelpunkt der Ellipse, der innere Schnittpunkt ein Scheitelpunkt der Hyperbel.

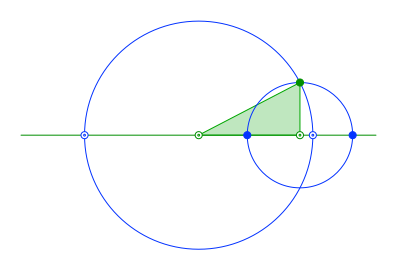
Abb. 3: Kleiner Kreis

Nun zeichnen wir die Ellipse mit den beiden Brennpunkten und dem Scheitelpunkt (Abb. 4).

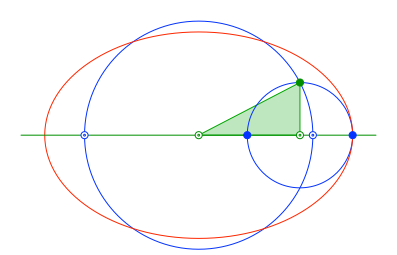
Abb. 4: Ellipse

Entsprechend zeichnen wir mit denselben Brennpunkten die Hyperbel (Abb. 5).

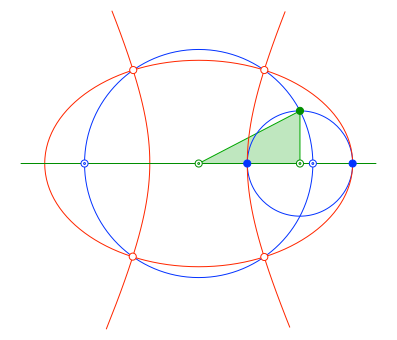
Abb. 5: Hyperbel. Schnittpunkte

Der große Kreis, die Ellipse und die Hyperbel haben vier gemeinsame Schnittpunkte.

3 Beweis

Für den rechnerischen Beweis verwenden wir die Bezeichnungen der Abbildung 6.

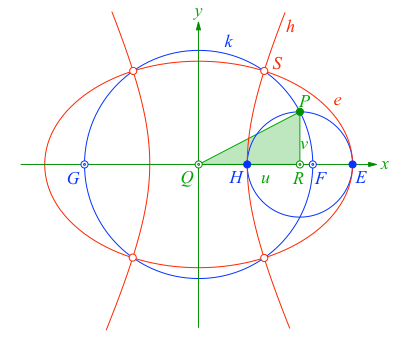
Abb. 6: Bezeichnungen

Das rechtwinklige Dreieck hat die Kathetenlängen u und v. Die Ecken P, Q, R des rechtwinkligen Dreieckes haben die Koordinaten:

Die Hypotenuse, und das ist auch der Radius des Kreises k, hat die Länge:

Damit ergibt sich für den Kreis k die Kreisgleichung:

Für die Brennpunkte F und G ergeben sich die Koordinaten:

Für die Scheitelpunkte E beziehungsweise H erhalten wir:

Die Ellipse e hat die lange Halbachse u + v und die halbe Brennpunktweite:

Damit ergibt sich für die kurze Halbachse der Ellipse:

Die Ellipse e hat also die Gleichung:

Für die Hyperbel h erhalten wir analog die Gleichung:

Mit einiger Rechnung ergibt sich aus den beiden Gleichungen für die Schnittpunkte von Ellipse und Hyperbel die Koordinaten:

Diese Koordinaten passen auch in die Kreisgleichung. Damit ist die Schnittpunkteigenschaft gezeigt.