1 Worum geht es?

Schnittpunkte von drei Kegelschnitten (Kreis, Ellipse, Hyperbel).

2 Konstruktionsgang

Wir beginnen mit einem Kreis mit einem Durchmesser und den beiden diametralen Schnittpunkten (Abb. 1). Die beiden diametralen Schnittpunkte verwenden wir später als Brennpunkte der Ellipse und der Hyperbel.

Abb. 1: Kreis mit Durchmesser

Wir passen ein Quadrat so ein, dass zwei diametrale Quadratecken auf dem Kreis und die anderen beiden auf dem Durchmesser liegen (Abb. 2).

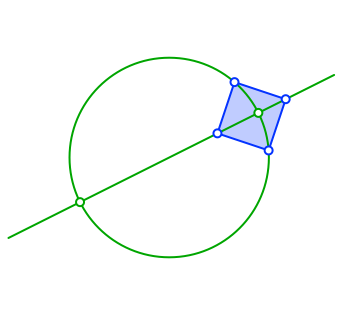
Abb. 2: Quadrat einpassen

Und nun zeichnen wir eine Ellipse mit den beiden diametralen Kreispunkten als Brennpunkten. Die Ellipse soll durch die außenliegende Quadratecke verlaufen (Abb. 3).

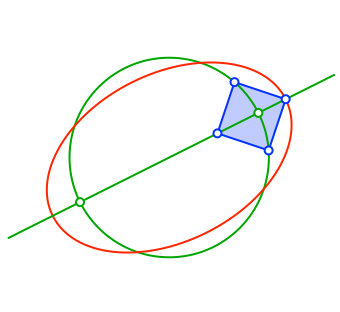
Abb. 3: Ellipse

Die Hyperbel hat dieselben Brennpunkte wie die Ellipse, verläuft aber durch die innere Quadratecke (Abb. 4).

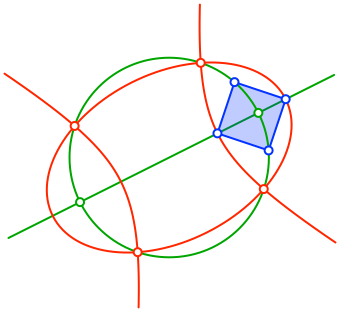
Abb. 4: Hyperbel

Der Kreis, die Ellipse und die Hyperbel haben vier gemeinsame Schnittpunkte.

Die Größe des eingepassten Quadrates kann variieren (Abb. 5 und 6).

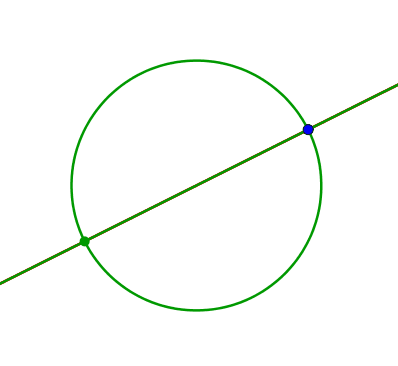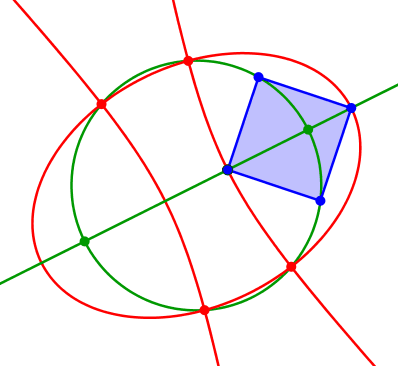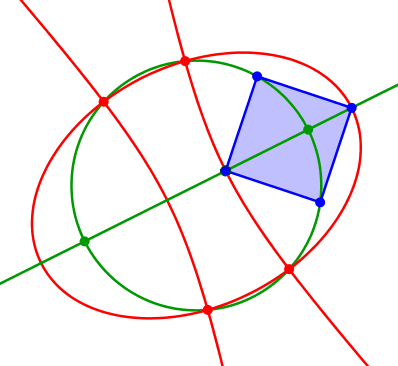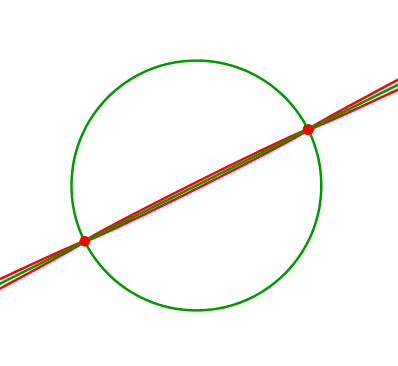
Abb. 5: Variation des Quadrates

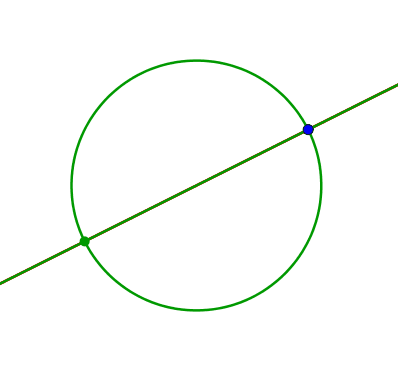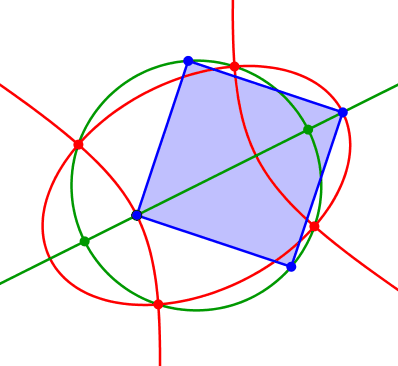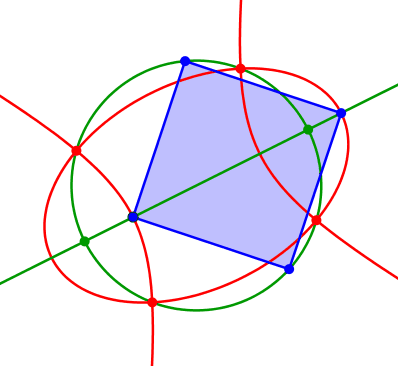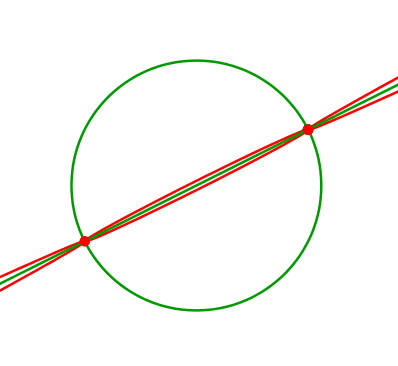
Abb. 6: Überschreiten der Mitte

3 Beweis

Der Beweis geht rechnerisch wie hier.

Weblink

Hans Walser: Schnittpunkt

http://www.walser-h-m.ch/hans/Miniaturen/S/Schnittpunkt4/Schnittpunkt4.html