Hans Walser, [20221118]

Schnittpunkt

1 Worum geht es?

Schnittpunkte von drei Kegelschnitten (Ellipse, zwei Parabeln).

2 DIN-Ellipse

Unter der DIN-Ellipse verstehen wir die Ellipse mit dem Achsenverhältnis √2 : 1. Im Folgenden einige Eigenschaften der DIN-Ellipse.

Die Ellipse lässt sich in ein Rechteck im DIN-Format einpassen (Abb. 1).

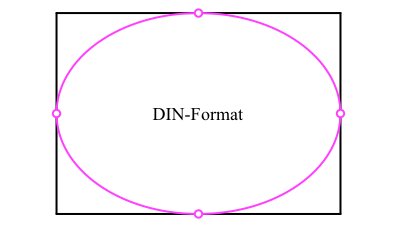
Abb. 1: Einpassen ins DIN-Format

Die Brennpunkte liegen auf dem Inkreis.

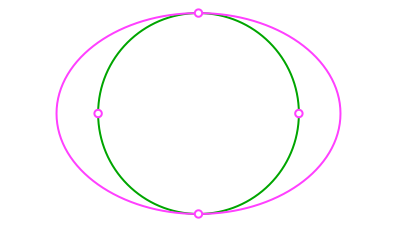
Abb. 2: Brennpunkte auf dem Inkreis

Die Krümmungskreise in den spitzen Scheiteln haben die halbe lange Halbachse der DIN-Ellipse als Radius (Abb. 3).

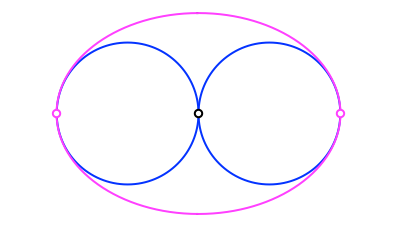
Abb. 3: Krümmungskreise in den spitzen Scheiteln

Die Krümmungskreise in den stumpfen Scheiteln haben die doppelte kurze Halbachse der DIN-Ellipse als Radius (Abb. 4).

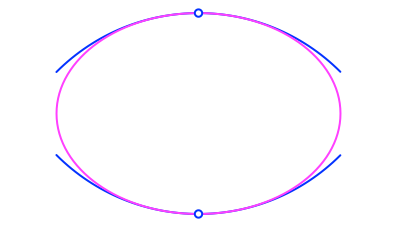
Abb. 4: Krümmungskreise in den stumpfen Scheiteln

Die Figur lässt sich in einen diagonalen Quadratraster einpassen (Abb.5).

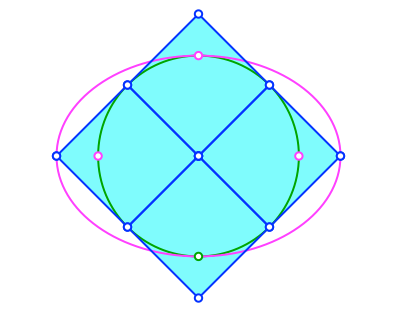
Abb. 5: Im Quadratraster

Wir werden die DIN-Ellipse in der folgenden Schnittpunkt-Figur verwenden.

3 Parabel

Eine Parabel ist durch ihren Brennpunkt und ihren Scheitelpunkt festgelegt. Das geht so: durch den Brennpunkt (grün in Abb. 6) und den Scheitelpunkt (blau) ist die Symmetrieachse der Parabel gegeben.

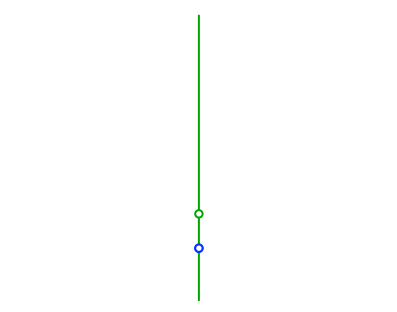
Abb. 6: Brennpunkt, Scheitelpunkt und Symmetrieachse

Nun spiegeln wir den Brennpunkt am Scheitelpunkt und legen durch den Spiegelpunkt die Leitlinie rechtwinklig zur Symmetrieachse (Abb. 7).

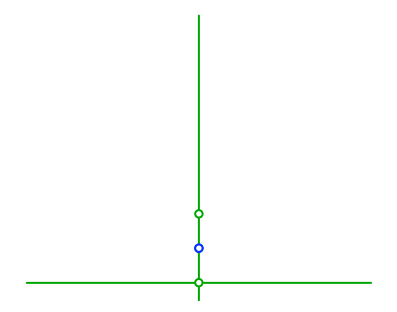
Abb. 7: Leitlinie

Durch Brennpunkt und Leitlinie ist die Parabel mit der Abstandsdefinition gegeben (Abb. 8).

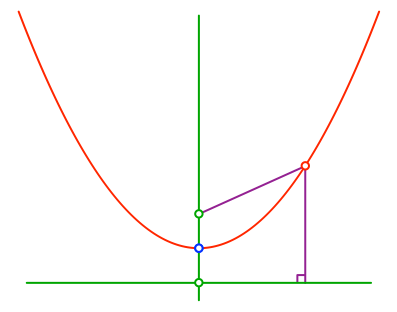
Abb. 8: Parabel

In der folgenden Schnittpunkt-Figur werden wir die beiden Parabeln über Brennpunkt und Scheitelpunkte definieren.

4 Konstruktionsgang

Wir beginnen mit der DIN-Ellipse, ihrem Inkreis und der senkrechten Symmetrieachse (Abb. 9). Den unteren Schnittpunkt der Symmetrieachse mit der Ellipse und dem Inkreis werden wir als gemeinsamen Brennpunkt der beiden Parabeln verwenden.

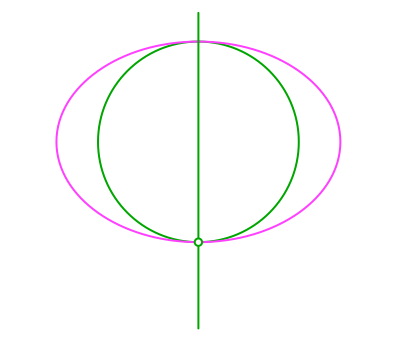
Abb. 9: Konstruktionsbeginn

Nun passen wir ein beliebiges Quadrat so ein, dass zwei diametrale Ecken auf der Symmetrieachse liegen und die beiden anderen Ecken auf dem Inkreis (Abb. 10). Die Diagonalenlänge des Quadrates darf allerdings nicht größer als der Durchmesser des Inkreises sein.

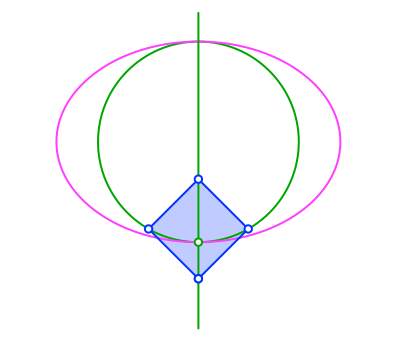
Abb. 10: Quadrat einpassen

Weiter passen wir eine erste Parabel mit dem schon definierten Brennpunkt und dem Scheitelpunkt in der unteren Ecke des Quadrates ein (Abb. 11).

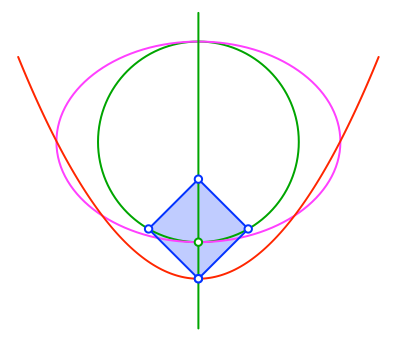
Abb. 11: Erste Parabel

Die zweite Parabel hat denselben Brennpunkt. Der Scheitelpunkt ist die obere Ecke des Quadrates (Abb. 12).

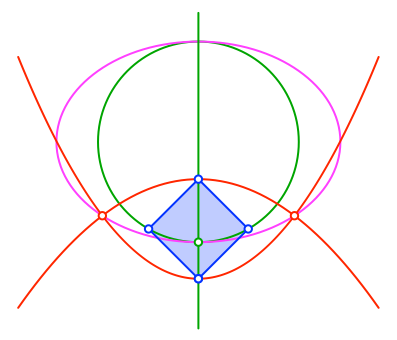
Abb. 12: Zweite Parabel

Die beiden Parabeln und die DIN-Ellipse haben zwei gemeinsame Schnittpunkte.

Beweis fehlt. Erhärtet mit GDS.

Die Abbildung 13 illustriert die Schnittpunkt-Figur bei Variation des blauen Quadrates.

Abb. 13: Variation des Quadrates

5 Sonderfälle

5.1 Spitze Scheitel

Wir passen in den Inkreis der DIN-Ellipse ein gleichseitiges Dreieck mit der Spitze im oberen stumpfen Scheitel der Ellipse ein (Abb. 14).

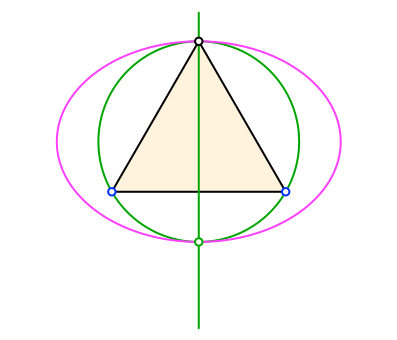
Abb. 14: Gleichseitiges Dreieck

Und nun passen wir das blaue Quadrate so ein, dass seine horizontale Diagonale auf die Grundlinie des gleichseitigen Dreiecks zu liegen kommt (Abb. 15).

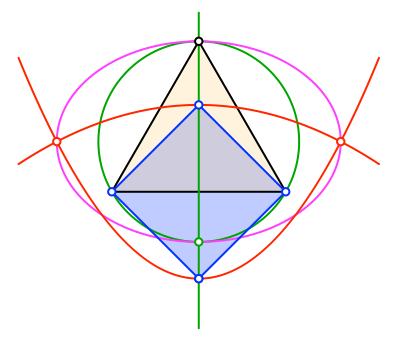
Abb. 15: Spezielle Lage des blauen Quadrates

In dieser Situation sind die beiden Schnittpunkte der DIN-Ellipse und der beiden Parabeln die spitzen Scheitel der Ellipse.

5.2 Tangenten

Wir passen das blaue Quadrat so ein, dass seine obere Ecke im Mittelpunkt des Inkreises der DIN-Ellipse liegt (Abb. 16). Die Seitenlänge des Quadrates ist nun gleich dem Radius des Inkreises und gleich der kurzen Halbachse der Ellipse. Es entspricht auch einem Quadrat des Quadratrasters der Abbildung 5.

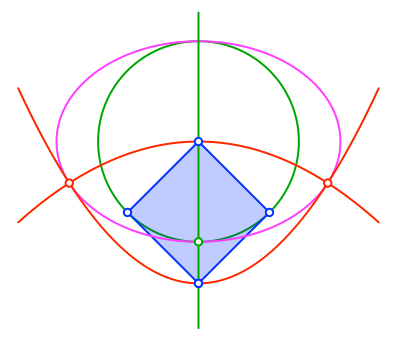
Abb. 16: Spezielles Quadrat

Die unteren beiden Seiten des Quadrates sind nun tangential an den Inkreis. Und die nach oben offene Parabel ist tangential an die Ellipse.

Weblink

Hans Walser: Schnittpunkt

http://www.walser-h-m.ch/hans/Miniaturen/S/Schnittpunkt4/Schnittpunkt4.html

Hans Walser: Schnittpunkt

http://www.walser-h-m.ch/hans/Miniaturen/S/Schnittpunkt5/Schnittpunkt5.html

Hans Walser: Schnittpunkt

http://www.walser-h-m.ch/hans/Miniaturen/S/Schnittpunkt7/Schnittpunkt7.html

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.