Hans Walser, [20221119]

Schnittpunkt

Idee und Anregung: Zvonimir Durcevic, Wien

1 Worum geht es?

Gemeinsame Schnittpunkte von zwei parallelen Geraden, einer Ellipse und einer Hyperbel. In einem Sonderfall erscheint der Goldene Schnitt

2 Konstruktionsweg

In den Punkten F und G zeichnen wir je die Senkrechte zur Geraden FG (Abb. 1). Diese beiden Senkrechten sind natürlich parallel zueinander. Die Punkte F und G werden wir später als gemeinsame Brennpunkte der Ellipse und der Hyperbel verwenden.

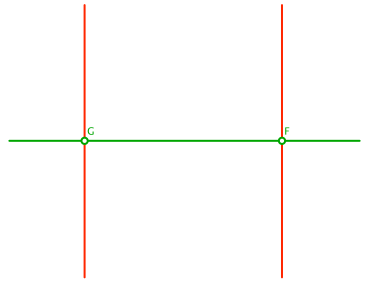
Abb. 1: Gerade mit Senkrechten

Vom Mittelpunkt M der Strecke FG aus strecken wir den Punkt F mit einem beliebigen Faktor t > 1. Dies gibt den Bildpunkt E (Abb. 2). Ebenso strecken wir den Punkt F mit dem Kehrwert 1/t und erhalten den Punkt H. Die beiden Punkte E und H verwenden wir als Scheitelpunkte für die Ellipse beziehungsweise die Hyperbel. Der Faktor t dient im Folgenden als Parameter der Figur.

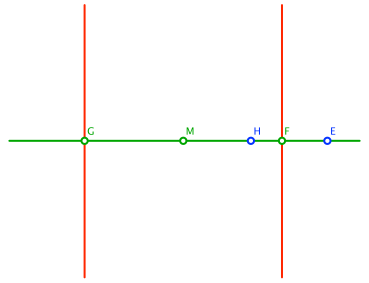
Abb. 2: Scheitelpunkte

Nun zeichnen wir die Ellipse mit den Brennpunkten F und G durch E (Abb. 3).

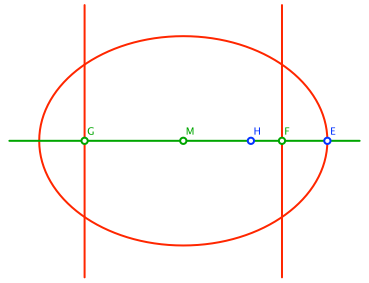
Abb. 3: Ellipse

Analog zeichnen wir die Hyperbel mit denselben Brennpunkten, aber durch H (Abb. 4).

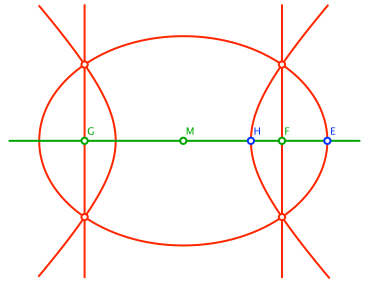
Abb. 4: Hyperbel

Die beiden parallelen Geraden, die Ellipse und die Hyperbel haben vier Punkte gemeinsam.

Die Abbildung 5 illustriert die Situation bei Variation des Parameters t.

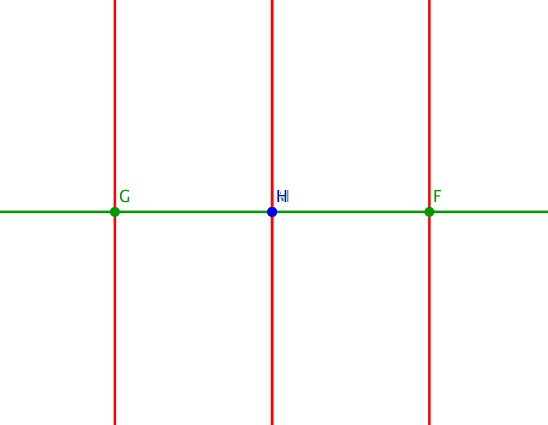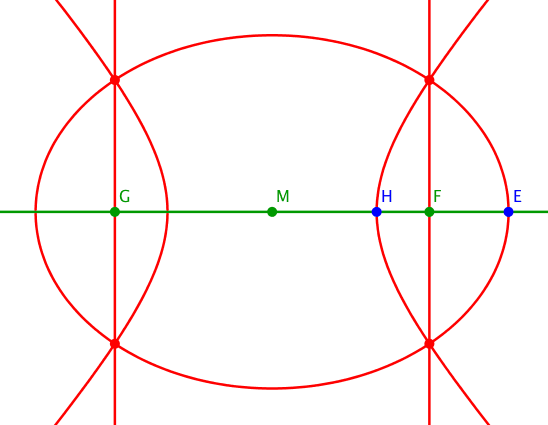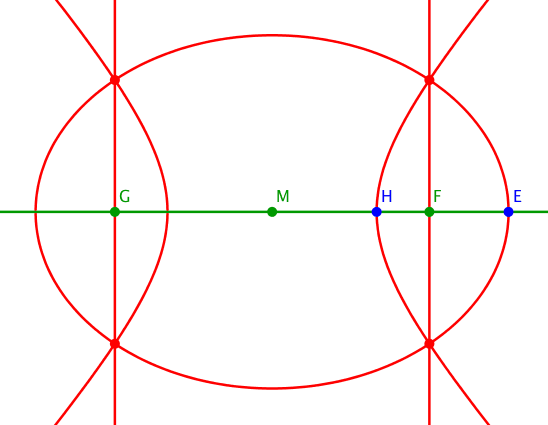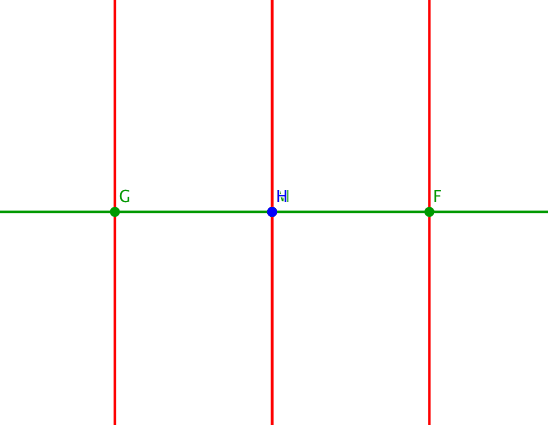
Abb. 5: Variation des Parameters

3 Beweis

Der Beweis geht rechnerisch im kartesischen Koordinatensystem der Abbildung 6.

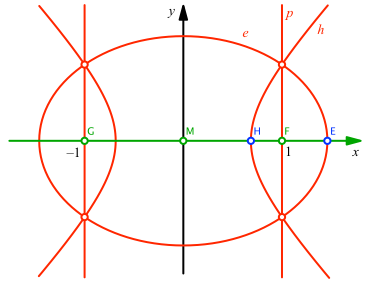
Abb. 6: Koordinatensystem

Die beiden Brennpunkte F und G der Ellipse e und der Hyperbel h haben die Koordinaten:

Der Scheitelpunkt E der Ellipse e hat die Koordinaten:

Daraus ergibt sich für die Ellipse e die Koordinatengleichung:

Der Scheitelpunkt H der Hyperbel h hat die Koordinaten:

Daraus ergibt sich für die Hyperbel h die Koordinatengleichung:

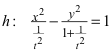
Für die vier Schnittpunkte der Ellipse e mit der Hyperbel h erhalten wir:

Diese Punkte liegen auf den Geraden p mit den Gleichungen:

Dies war zu zeigen.

4 Sonderfall Quadrat

Für welchen Parameterwert t bilden die vier Schnittpunkte ein Quadrat? (Abb. 7)

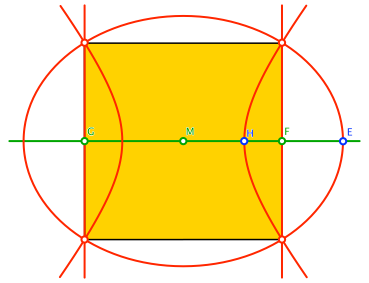
Abb. 7: Quadrat

Die y-Koordinaten der Schnittpunkte müssen betragsmäßig den Wert 1 haben. Aus der Bedingung

erhalten wir die biquadratische Gleichung:

Die Lösung t > 1 ist:

Dies ist der Goldene Schnitt. In der Abbildung 7 teilt also der Punkt F die Strecke ME im Verhältnis des Goldenen Schnittes. Ebenso teilt der Punkt H die Strecke MF im Goldenen Schnitt.

5 Variante

Die stilistisch etwas unschönen Streckungen mit dem Parameter t und dessen Kehrwert können geometrisch mit einem rechtwinkligen Dreieck angegangen werden (Abb. 8).

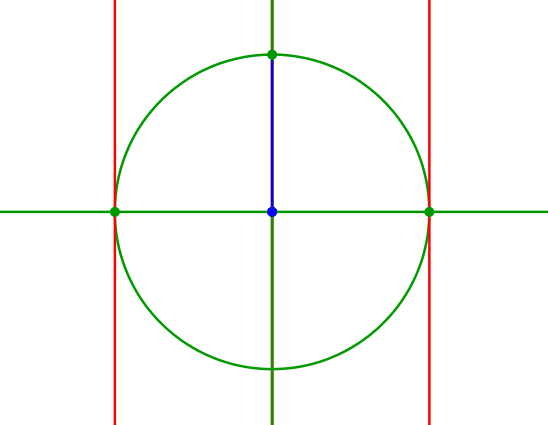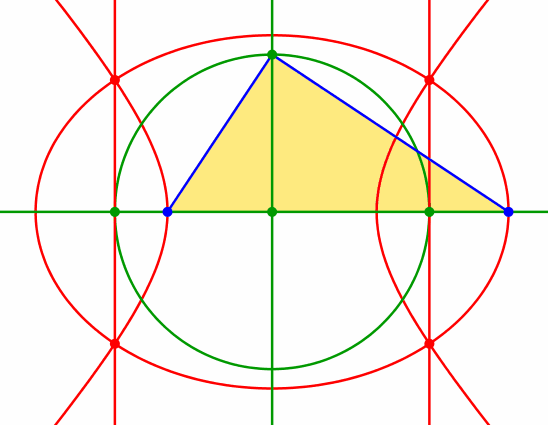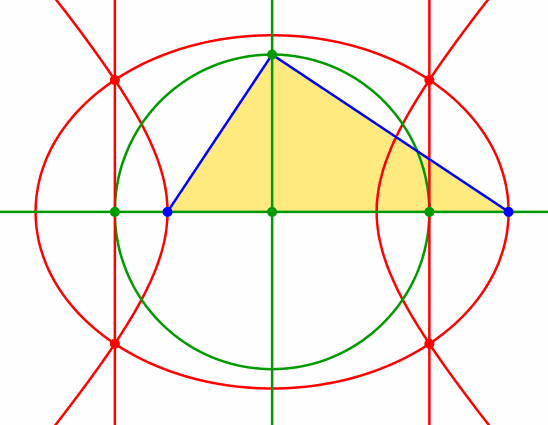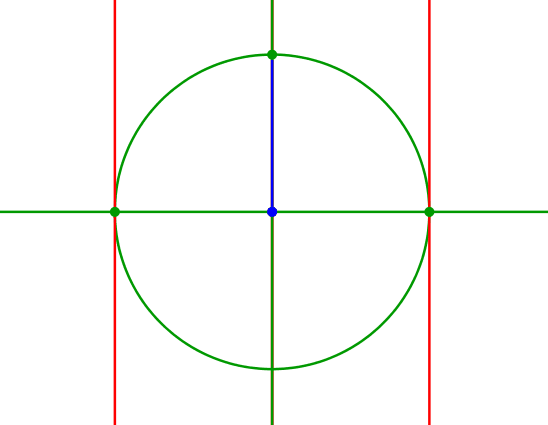
Abb. 8: Variante mit rechtwinkligem Dreieck

Weblinks

Hans Walser: Schnittpunkt

http://www.walser-h-m.ch/hans/Miniaturen/S/Schnittpunkt5/Schnittpunkt5.html

Literatur

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.