Hans Walser, [20240424]

Schnittpunkt

1 Worum es geht

Drei verschiedene Konstruktionswege für denselben Schnittpunkt im Dreieck.

Beim ersten Konstruktionsweg versagt GeoGebra.

2 Die Konstruktionswege

2.1 Erster Konstruktionsweg

Wir beginnen einem Dreieck (Abb. 1.1).

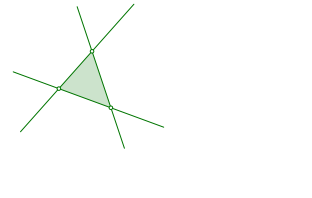
Abb. 1.1: Startdreieck

Mit den äußeren Winkelhalbierenden konstruieren wir die Mittelpunkte der Ankreise (blau in Abb. 1.2).

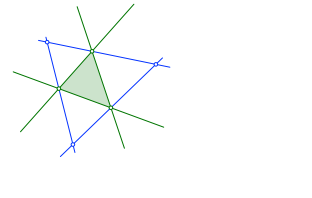
Abb. 1.2: Mittelpunkte der Ankreise

Von den Mittelpunkten aus fällen wir die Lote auf die Dreieckseiten und erhalten so die Radien der Ankreise (magenta in Abb. 1.3).

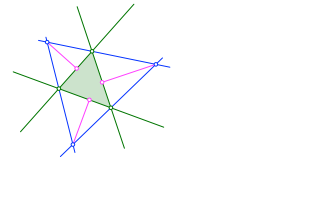
Abb. 1.3: Radien der Ankreise

Nun zeichnen wir die Ankreise (Abb. 1.4).

Abb. 1.4: Ankreise

Wir bestimmen die Berührungspunkte der Ankreise mit den verlängerten Dreieckseiten (blau in Abb. 1.5). Ich habe dies mit dem Button Schnittpunkt gemacht, habe also die Kreise mit den jeweiligen verlängerten Dreieckseiten geschnitten. Es gibt jeweils nur einen Schnittpunkt, eben den Berührungspunkt.

Abb. 1.5: Berührungspunkte

Durch benachbarte Berührungspunkte zeichnen wir Geraden (orange in Abb. 1.6), die wir zu einem Dreieck ergänzen.

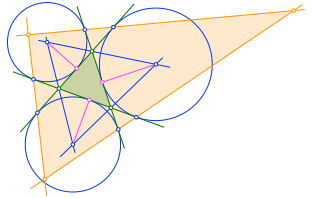
Abb. 1.6: Dreieckseiten durch Berührpunkte

Nun verbinden wir die Ecken des orangen Dreiecks je mit den gegenüberliegenden Ecken des grünen Startdreiecks (rot in Abb. 1.7). Die drei roten Verbindungsstrecken scheinen einen gemeinsamen Schnittpunkt zu haben.

Nun ist es allerdings so, dass GeoGebra die Schnittpunkteigenschaft verneint. Vorgehen: Zwei der drei Verbindungsstrecken miteinander schneiden, mit dem Button Beziehung? prüfen, ob der Schnittpunkt auch auf der dritten Verbindungsstrecke liegt. GeoGebra verneint dies.

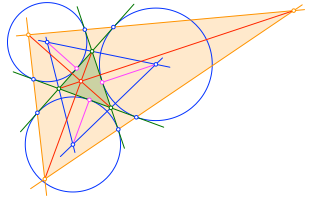
Abb. 1.7: Schnittpunkt?

2.2 Zweiter Konstruktionsweg

Wir beginnen mit demselben Dreieck (Abb. 2.1).

Abb. 2.1: Startdreieck

Wir konstruieren wiederum die Schnittpunkte der äußeren Winkelhalbierenden (blau in Abb. 2.).

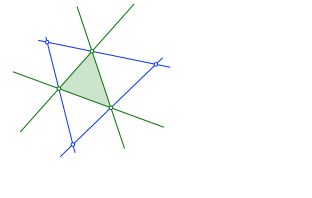
Abb. 2.2: Äußere Winkelhalbierende

Von den Schnittpunkten aus fällen wir die Lote auf die verlängerten Dreieckseiten (magenta in Abb. 2.3).

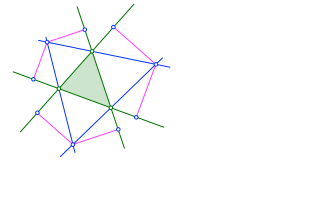
Abb. 2.3: Lote

Durch benachbarte Lotfußpunkte zeichnen wir Geraden (orange in Abb. 2.4), die wir zu einem Dreieck ergänzen.

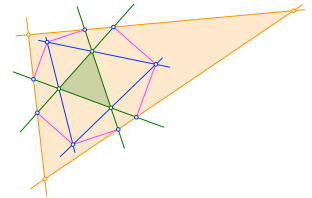
Abb. 2.4: Dreieckseiten durch Lotfußpunkte

Nun verbinden wir die Ecken des orangen Dreiecks je mit den gegenüberliegenden Ecken des grünen Startdreiecks (Abb. 2.5). Die drei roten Verbindungsstrecken haben einen gemeinsamen Schnittpunkt. Dies wird durch GeoGebra (numerisch) bestätigt.

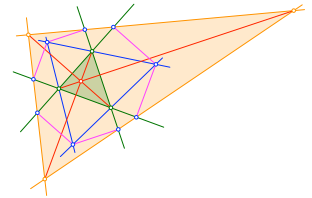
Abb. 2.5: Schnittpunkt

2.3 Dritter Konstruktionsweg

Für den dritten Konstruktionsweg benötigen wir den halben Umfang. In der üblichen Schreibweise ist dies s = ½(a + b + c). Der halbe Umfang s kann in GeoGebra entweder konstruktiv oder rechnerisch bestimmt werden. Ich habe den rechnerischen Weg gewählt.

Wir beginnen wiederum mit demselben Dreieck (Abb. 3.1).

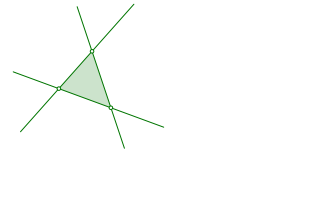
Abb. 3.1: Startdreieck

Nun zeichnen wir drei Kreissektoren, alle mit dem gleichen Radius s (blau in Abb. 3.2).

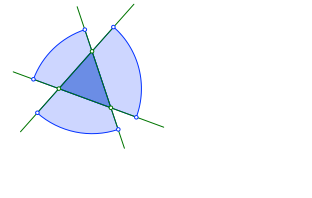
Abb. 3.2: Kreissektoren

Durch benachbarte Eckpunkte der Kreissektoren zeichnen wir Geraden (orange in Abb. 3.3), die wir zu einem Dreieck ergänzen.

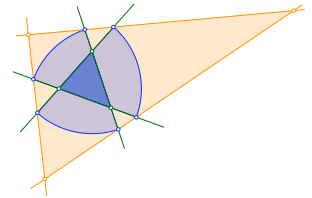
Abb. 3.3: Dreieckseiten durch Sektorenecken

Nun verbinden wir die Ecken des orangen Dreiecks je mit den gegenüberliegenden Ecken des grünen Startdreiecks (Abb. 3.4). Die drei roten Verbindungsstrecken haben einen gemeinsamen Schnittpunkt. Dies wird durch GeoGebra bestätigt.

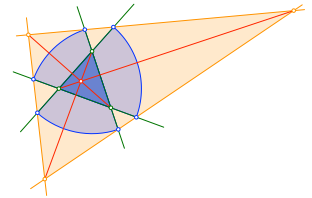
Abb. 3.4: Schnittpunkt

3 Kommentare

Die drei Konstruktionswege sind geometrisch gleichwertig.

Ich vermute, dass der wunde Punkt im ersten Konstruktionsweg bei der Bestimmung der Berührungspunkte (Abb. 1.5) liegt. Als „Schnittpunkt“ ist das ein extrem „schleifender Schnitt“.

Im Geometrie-Unterricht (Sekundarstufe 1) mussten wir immer zuerst den Berührungsradius zeichnen, also den Radius zum Berührungspunkt. Der Lehrer kontrollierte dies mit der Lupe. Sein Argument war, dass die zuerst gezeichnete Linie dünner ist als die nachfolgende, weil sich der Bleistift abnützt. Wenn man also den Berührungsradius erst hinterher zeichnete, musste man vorgängig den Bleistift nachspitzen, damit der Lehrer nichts merkte.

Unser Schnittpunkt ist der Höhenschnittpunkt des Startdreieckes. Wer Lust hat, kann das beweisen. Auch in diesem Kontext spielt GeoGebra mit. Beim ersten Konstruktionsweg wird die Orthogonalität der roten Verbindungsstrecken zu den Dreieckseiten nicht wahrgenommen, in den beiden anderen Konstruktionswegen hingegen schon.

Weblinks

Hans Walser: Schnittpunkte

https://walser-h-m.ch/hans/Schnittpunkte/