Hans Walser, [20160823]
Schnittpunkte in Pythagoras-Beweisen
1 Worum geht es?
In den źblichen Beweisfiguren fźr den Satz des Pythagoras lassen sich Schnittpunkte von drei Geraden einzeichnen. Die Beweise der Schnittpunkteigenschaft sind sehr einfach.
2 Die Schnittpunkte
2.1 In der Zerlegung des Quadrates
Die Abbildung 1 zeigt zwei Zerlegungen desselben Quadrates. Damit kann der Satz des Pythagoras im Sinne eines ErgŠnzungsbeweises gezeigt werden.
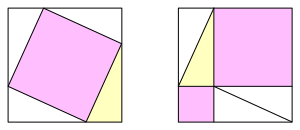
Abb. 1: ErgŠnzungsbeweis fźr den Satz des Pythagoras
Im Gerźst der Figur rechts finden wir einen Schnittpunkt von drei Geraden (Abb. 2). Stimmt der Schnittpunkt?
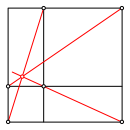
Abb. 2: Schnittpunkt?
2.2 In der Beweisfigur des Euklid
Die Abbildung 3 zeigt die Illustration des Beweises von Euklid (Euklid 1980, Erstes Buch, ¤ 47) fźr den Satz des Pythagoras.
Wir sehen einen Schnittpunkt von drei Geraden. Stimmt er?

Abb. 3: Schnittpunkt?
3 Beweise der Schnittpunkteigenschaft
3.1 Zerlegungsfigur
Wir kšnnen in die Figur der Abbildung 2 ein Dreieck einzeichnen (gelb in Abbildung 4), dessen Hšhenschnittpunkt der zur Diskussion stehende Punkt ist.
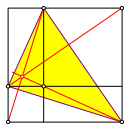
Abb. 4: Hšhenschnittpunkt
3.2 Figur von Euklid
Wir kšnnen die Figur der Abbildung 3 etwas ergŠnzen und dann ebenfalls ein Dreieck einzeichnen (gelb in Abbildung 5), dessen Hšhenschnittpunkt der zur Diskussion stehende Punkt ist.
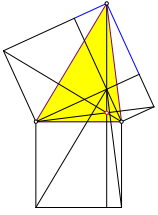
Abb. 5: Hšhenschnittpunkt
Die beiden gelben Dreiecke der Abbildungen 4 und 5 sind (bei kongruenten rechtwinkligen Dreiecken als Ausgangsfigur) kongruent. Die beiden Schnittpunkte sind im Wesentlichen dieselben.
Literatur
Euklid (1980): Die Elemente. Nach Heibergs Text aus dem Griechischen źbersetzt und herausgegeben von Clemens Thaer. Darmstadt: Wissenschaftliche Buchgesellschaft. ISBN 3-534-01488-X