1 Worum es geht

Auf der Basis eines Dreiecks führen Hyperbeln und Ellipsen zu vielen Schnittpunkten von drei oder mehr Kurven.

Ebenso erhalten wir kollineare Punkte, zum Beispiel drei oder mehr Punkte auf einer Geraden.

Ohne Beweis. Verifikation mit DGS.

2 Ausgangslage

Wir beginnen mit einem Dreieck in der Farbgebung der Abbildung 1.

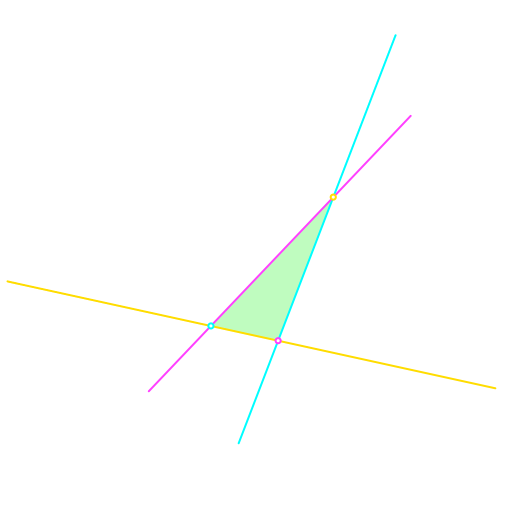
Abb. 1: Startdreieck

3 Hyperbeln

Wir zeichnen die Hyperbel, welche den hellblauen und den magenta Eckpunkt des Dreiecks als Brennpunkte hat und durch den gelben Dreieckspunkt verläuft (Abb. 2). Die Scheitelpunkte der Hyperbel liegen auf der gelben Dreieckseite.

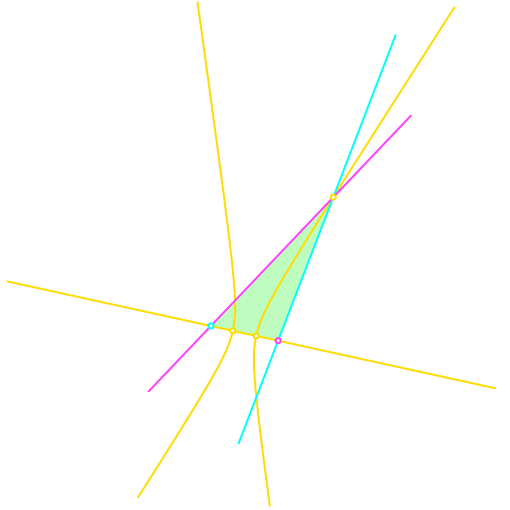
Abb. 2: Hyperbel

Mit zyklischer Farbvertauschung zeichnen wir die beiden anderen Hyperbeln (Abb. 3). Wir erhalten zwei Dreifarben-Schnittpunkte (rot in Abb. 3).

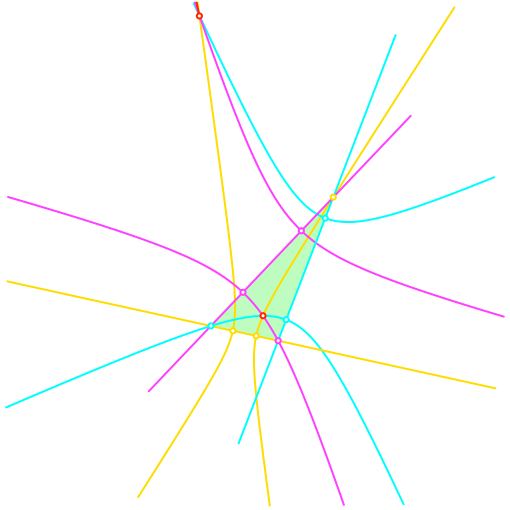
Abb. 3: Die drei Hyperbeln

4 Inkreis

Der Inkreis berührt die Dreiecksseiten in Scheitelpunkten der Hyperbeln (Abb. 4). Der Inkreismittelpunkt liegt auf der Geraden durch die beiden Dreifarben-Schnittpunkte.

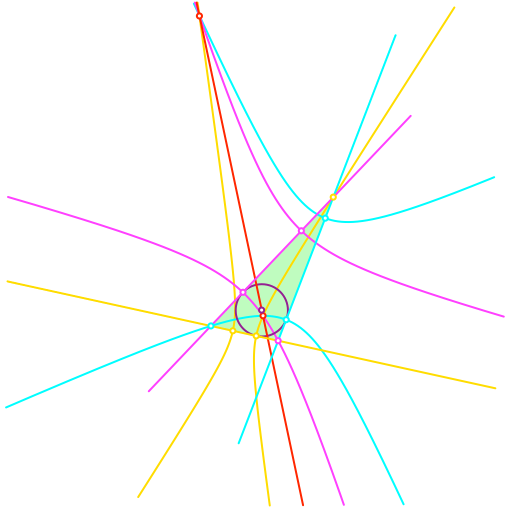
Abb. 4: Inkreis

5 Ellipsen

Analog zur Hyperbel zeichnen wir eine Ellipse, welche den hellblauen und den magenta Eckpunkt des Dreiecks als Brennpunkte hat und durch den gelben Dreieckspunkt verläuft (Abb. 5). Die Scheitelpunkte der spitzen Ellipsenscheitel liegen auf der gelben Dreieckseite.

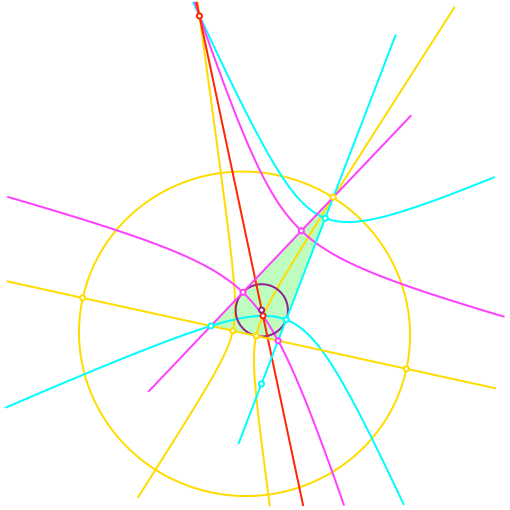
Abb. 5: Ellipse

Mit zyklischer Farbvertauschung zeichnen wir die beiden anderen Ellipsen (Abb. 6). Wir erhalten sechs zusätzliche Dreifarben-Schnittpunkte. An diesen neuen Dreifarben-Schnittpunkte sind je zwei Ellipsen und eine Hyperbel beteiligt. Je zwei Dreifarben-Schnittpunkte gehören zu denselben drei Kegelschnitten.

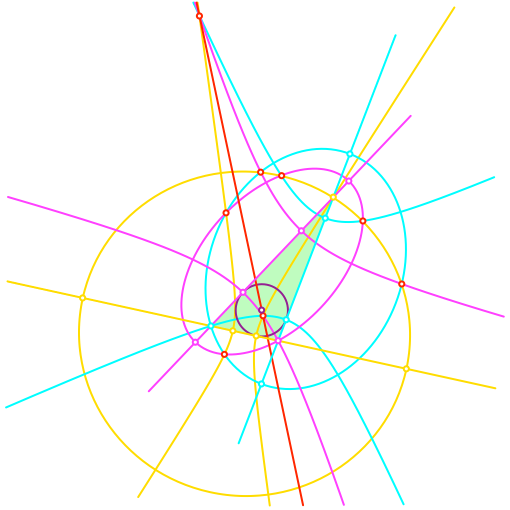
Abb. 6: Die drei Ellipsen

6 Geraden

Wir legen je eine Gerade durch die beiden zu denselben drei Kegelschnitten gehörenden Dreifarben-Schnittpunkten (rot in Abb. 7). Diese drei Geraden sowie die Gerader durch die beiden Dreifarben-Schnittpunkte der drei Hyperbeln (Abb. 4) haben einen gemeinsamen Schnittpunkt.

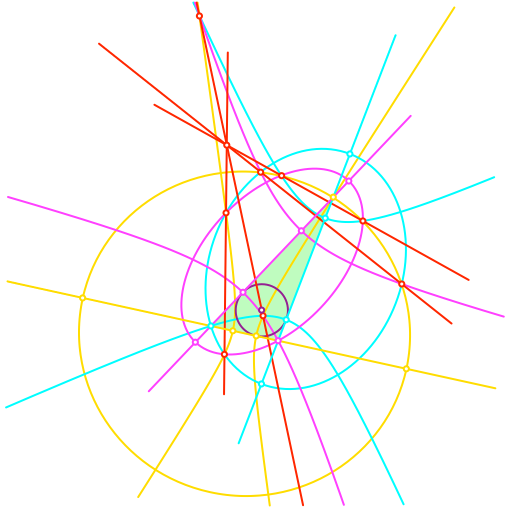
Abb. 7: Geraden

Wir haben jetzt also vier Geraden, welche durch je zwei Dreifarben-Schnittpunkte der beteiligen Kegelschnitte definiert sind, und die einen gemeinsamen Schnittpunkt haben.

7 Ankreise

Der Ankreis an die gelbe Dreiecksseite verläuft durch drei verschiedenfarbige Kegelschnittscheitelpunkte (Abb. 8). Sein Mittelpunkt liegt auf einer der roten Geraden durch zwei Dreifarben-Schnittpunkte.

Abb. 8: Ankreis

Analog mit zyklischer Farbvertauschung für die beiden anderen Ankreise (Abb. 9).

Abb. 9: Die drei Ankreise

Wir haben also vier Geraden, welche durch je zwei Dreifarben-Schnittpunkte der beteiligen Kegelschnitte definiert sind, einen gemeinsamen Schnittpunkt haben und je einen In- oder Ankreismittelpunkt enthalten.

8 Umkreis

Der Umkreis verläuft durch Schnittpunkte gleichfarbiger Hyperbeln und Ellipsen (Abb. 10 und 11).

Abb. 10: Umkreis

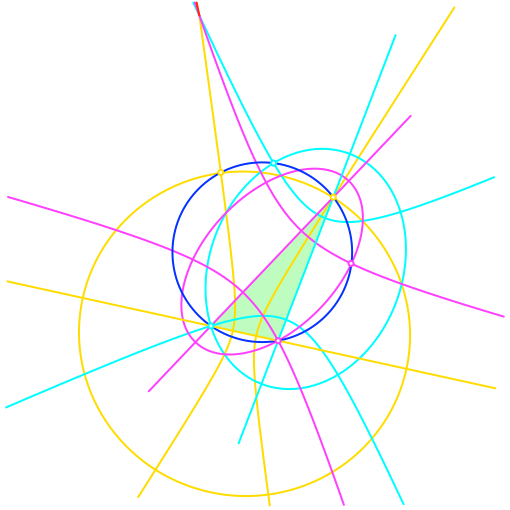
Abb. 11: Umkreis als Sechspunktekreis

Weblinks

Hans Walser: Schnittpunkte

https://walser-h-m.ch/hans/Schnittpunkte/index.html