Hans Walser, [20180107]

Schrägkanten-Modelle

Idee und Anregung: Thomas Müller, KPH Krems

1 Worum geht es

Aus einem einzigen Streifen können wir mit geeigneten Faltlinien Modelle bauen, deren Ecken auf Ecken der platonischen Körper liegen. Die Modelle halten in der Regel ohne Bindemittel und sind leicht wieder zerlegbar.

Die Methode erlaubt auch eine Faltkonstruktion des regelmäßigen Siebenecks.

2 Oktaeder

Für das Oktaeder arbeiten wir mit einem Streifen der Abbildung 1.

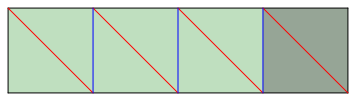
Abb. 1: Streifen für das Oktaeder

Der Streifen besteht aus drei Quadraten plus einem Überlappungsquadrat. Dieses ist mit dem ersten Quadrat zu identifizieren.

Zwischen den Quadraten bringen wir Bergfalte (blau) an.

Weiter falten wir je eine der Diagonalen als Talfalte (rot). Die gefalteten Diagonalen müssen parallel sein.

Werden in der Abbildung 1 die Begriffe Bergfalte und Talfalte vertauscht, ergibt sich ein spiegelbildliches Modell.

Nun falten wir längs der kurzen (blauen) Faltkanten ganz zusammen und fixieren allenfalls provisorisch mit einer Büroklammer. Die Büroklammern können nach dem Zusammenbau wieder entfernt werden. Der Rest ergibt sich von selber.

Für das Modell der Abbildung 2 wurde Papier mit unterschiedlicher Färbung auf beiden Seiten verwendet.

Abb. 2: Oktaeder

Oft hält das Modell auch von selbst. Falls nicht, lassen wir eine Büroklammer stecken (Abb. 3) oder verleimen.

Abb. 3: Die einsame Büroklammer

Auf den ersten Blick sieht man das Oktaeder vielleicht nicht, sondern ein Antiprisma mit einem gleichseitigen Dreieck als Grund- und Deckfläche. Aber genau das ist ein Oktaeder.

Unser Modell enthält 9 der 12 Oktaederkanten. Dafür sind alle drei Diagonalen vorhanden und sichtbar. Die Abbildung 4a zeigt das Modell in der üblichen Oktaederansicht. Die Abbildung 4b zeigt die vorhandenen Kanten und Diagonalen. Die Diagonalen entstanden aus den roten Diagonalenfalten der Abbildung 1. Die blauen Kanten sind die drei Falten zwischen den Quadraten der Abbildung 1. Die schwarzen Kanten (wir haben zwei schwarze gleichseitige Dreiecke) sind die oberen und unteren Schnittkanten der Abbildung 1. Die drei zum Oktaeder noch fehlenden Kanten sind grün nachgetragen.

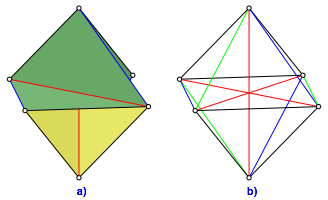
Abb. 4: Ansicht und Kantenschema

3 Würfel

Für den Würfel arbeiten wir mit einem Streifen gemäß Abbildung 5.

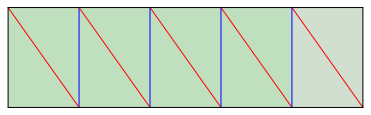
Abb. 5: Streifen für den Würfel

Die Rechtecke haben das Seitenverhältnis . Das ist das DIN-Format (Walser 2013b). Die blauen Faltkanten werden zu Seitenflächendiagonalen, die roten zu Raumdiagonalen des Würfels.

Die Abbildung 6 zeigt das zugehörige Modell. Es ist eine Art Doppelpyramide.

Abb. 6: Würfel

Die Abbildung 7 zeigt die Einbettung in den Würfel. Wir sehen, dass die vier senkrechten Würfelkanten fehlen und grün nachgetragen werden müssen.

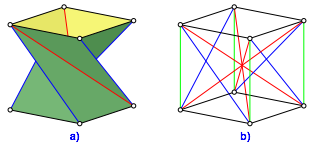
Abb. 7: Einbettung in den Würfel

4 Angebotskorb

Die Rechteckhöhen in der Abbildung 5 können beliebig verändert werden. Das Modell passt dann nicht mehr in einen Würfel sondern in ein Prisma mit quadratischer Grundfläche.

Solche Kartonmodelle dienen in Läden gelegentlich als Präsentier- und Angebotskörbe. Sie haben den Vorteil, dass sie für den Transport flachgelegt werden können. Im Kleinformat können sie auch als Behälter für Büromaterial benutzt werden (Abb. 8).

Abb. 8: Büromaterial

5 Nochmals Würfel

Für ein zweites Modell zum Würfel arbeiten wir mit einem Streifen gemäß der Abbildung 9. Die Rechtecke haben das Seitenverhältnis . Sie sind wiederum im DIN-Format, aber nun im Querformat.

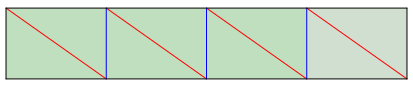
Abb. 9: Streifen für den Würfel

In der Abbildung 10 sehen wir das Modell von oben. Was hat das sichtbare gleichseitige Dreieck mit dem Würfel zu tun?

Abb. 10: Modell

Die Abbildung 11 zeigt die Einbettung in den Würfel. Die gleichseitigen Dreiecke oben und unten des Modells werden aus Seitenflächendiagonalen des Würfels gebildet.

Nur sechs der acht Würfelecken werden vom Modell erreicht.

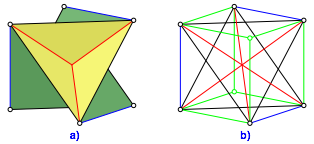
Abb. 11: Einbettung in den Würfel

6 Dodekaeder

Für das Dodekaeder arbeiten wir mit einem Streifen gemäß Abbildung 12. Die Rechtecke haben das Seitenverhältnis . Dabei ist der Goldene Schnitt (Walser 2013a).

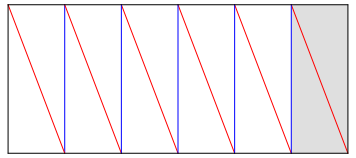
Abb. 12: Streifen für Dodekaeder

Die Abbildung 13 zeigt das Modell. Wie alle unsere Modelle ist es eine Art Doppelpyramide.

Abb. 13: Passt in ein Dodekaeder

Das Modell sieht zwar elegant aus, aber es hat nur zehn Ecken, nämlich das Grundfünfeck und das Deckfünfeck. Das Dodekaeder (Abb. 14) hat aber 20 Ecken.

Das Dodekaedermodell der Abbildung 14 besteht aus zwölf Pyramiden. Diese haben ihre Spitze gemeinsam im Zentrum. Sie sind kongruent zu den beiden Pyramiden des Modells der Abbildung 13.

Abb. 14: Dodekaeder

Das Modell der Abbildung 13 passt genau in die fünf Ecken des Grundfünfeckes des Dodekaeders der Abbildung 14 und die fünf Ecken des Deckfünfeckes. Die Abbildung 15 illustriert die Einbettung.

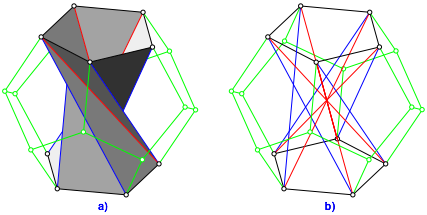
Abb. 15: Einbettung in das Dodekaeder

Die fehlenden zehn Ecken des Dodekaeders finden wir mit einem Streifen der Abbildung 16. Die Streifen haben ein Seitenverhältnis . Wir haben es wieder wie bei der Abbildung 5, wo es um den Würfel ging, mit dem DIN-Format zu tun. Die Überraschung legt sich, wenn wir uns überlegen, dass man auf dem Dodekaeder mit Seitenflächendiagonalen einen Würfel festlegen kann.

Abb. 16: Streifen für Dodekaeder

Die Abbildung 17 zeigt das zugehörige Modell.

Abb. 17: Passt in ein Dodekaeder

In der Abbildung 18 sehen wir die Einbettung in das Dodekaeder.

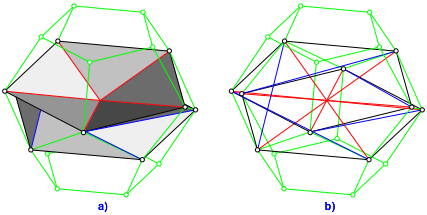
Abb. 18: Einbettung in das Dodekaeder

7 Ikosaeder

Für das Ikosaeder arbeiten wir mit einem Streifen der Abbildung 19. Die Rechtecke haben das Seitenverhältnis , sind also Goldene Rechtecke.

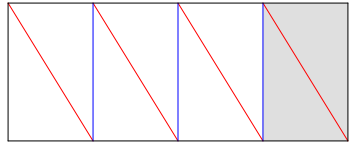
Abb. 19: Streifen für Ikosaeder

Die Abbildung 20 zeigt das Modell. Es passt in ein Ikosaeder (Abb. 21).

Abb. 20: Passt in ein Ikosaeder

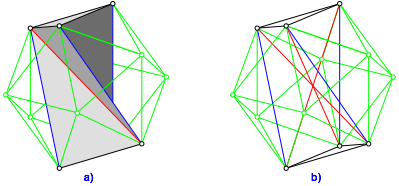
Abb. 21: Einbettung in das Ikosaeder

Es gibt auch eine andere Lösung. Dazu arbeiten wir mit dem Streifen der Abbildung 22. Die Rechtecke haben das Seitenverhältnis , sind also ebenfalls Goldene Rechtecke.

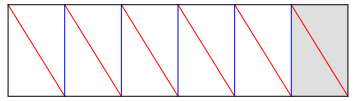
Abb. 22: Streifen für Ikosaeder

Die Abbildung 23 zeigt das Modell.

Abb. 23: Modell

Die Abbildung 24 zeigt die Einbettung in das Ikosaeder. Wer mit der Figur nicht klarkommt, bastelt ein Modell.

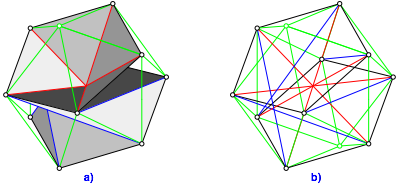
Abb. 24: Einbettung in das Ikosaeder

8 Tetraeder?

Das Tetraeder hat als einziges von den platonischen Polyedern keine parallelen Seitenflächen. Es hat keine Punktsymmetrie.

Daher können wir mit unserer Methode kein passendes Modell bauen.

Wir können aber das Tetraeder an seinem Mittelpunkt spiegeln. Zusammen mit dem Spiegelbild ergibt sich der Kepler-Stern. Der hat aber dieselben Ecken wie der Würfel. Unsere Modelle für den Würfel passen auch in den Keplerstern.

9 Flache regelmäßige Polygone

Wir können jedes regelmäßige Polygon mit unserer Methode bauen. Für das regelmäßige Dreieck arbeiten wir mit einem Streifen gemäß Abbildung 25. Die Rechtecke haben das Seitenverhältnis . Der stumpfe Diagonalenschnittwinkel ist 120°. Das ist ein Drittel des vollen Winkels.

Abb. 25: Streifen für Dreieck

Die Abbildung 26 zeigt das Modell.

Abb. 26: Dreieck

Für das regelmäßige Fünfeck arbeiten wir mit einem Streifen gemäß Abbildung 27. Die Rechtecke haben das Seitenverhältnis . Der spitze Diagonalenschnittwinkel ist 72°. Das ist ein Fünftel des vollen Winkels.

Abb. 27: Streifen für das Fünfeck

Die Abbildung 28 zeigt das Modell.

Abb. 28: Fünfeck

Wir sehen, wie der Hase läuft.

10 Allgemein

Wir können zu jedem Prisma mit einem regelmäßigen Vieleck gerader Eckenzahl als Grundfläche (exemplarisch ein Sechseck in Abb. 29a) und zu jedem Antiprisma mit einem regelmäßigen Vieleck ungerader Eckenzahl als Grundfläche (exemplarisch ein Siebeneck in Abb. 29b) ein Modell nach unserer Methode bauen.

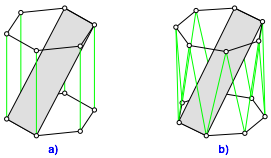
Abb. 29: Allgemeiner Fall

Der Streifen besteht aus den in der Abbildung 29 eingezeichneten Rechtecken. Für ein n-Eck als Grundfläche braucht es Rechtecke. Die Höhe der Rechtecke ist irrelevant.

11 Das regelmäßige Siebeneck

Das regelmäßige Siebeneck ist nach einem Satz von Gauß nicht mit Zirkel und Lineal konstruierbar. Hingegen können wir mit unserer Faltmethode ein Siebeneck konstruieren.

Abb. 30: Modell mit Siebeneck

Das Modell der Abbildung 30 wurde aus einem längs der langen Mittellinie halbierten DIN A4-Papier gefaltet (es geht auch mit anderen Rechteckformaten, insbesondere US Letter). Durch mehrmaliges Halbieren erfalten wir eine Folge von acht Rechtecken. Das genaue Seitenverhältnis der Rechtecke ist nicht relevant. Und dann geht es weiter wie gehabt. Die Abbildung 31 zeigt das Modell von der Büroklammerseite.

Abb. 31: Modell mit Büroklammer

Die Abbildung 32 schließlich zeigt das Modell von oben. Wir sehen das Siebeneck.

Abb. 32: Siebeneck

Literatur

Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.

Abbildungsnachweis

Abb. 8: Heinz Slepcevic, Graz

Alle übrigen Abbildungen durch den Autor