Hans Walser, [20220327]

Schraubenlinie

Anfrage: M. K., S.

1 Beispiel 1

Die Abwicklung einer Schraubenlinie soll durch die Punkte mit den Koordinaten (0,0), (1,2),   (2,4),   (3,6),   (4,8), (5,10), (6,12), (0,12), (1,14), (2,16), ... verlaufen. Man beachte den Hiatus bei der fett markierten Stelle.

Gefragt wir nach den relevanten Daten der Schraubenlinie.

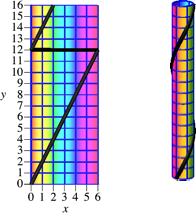
Die Abbildung 1 zeigt die Abwicklung und die Schraubenlinie.

Der horizontale schwarze Strich in der Abwicklung ist ein ästhetisches Scheusal. Der Strich bedeutet, dass die beiden Punkte (6,12), (0,12) in der Abwicklung zwar verschieden sind, aber auf dem Zylinder gleich. Sie sind zu „identifizieren“.

Abb. 1: Beispiel 1

Es ist:

Dabei ist Deltax die Breite der Abwicklung. Dies ist auch der Umfang des Zylinders.

Weiter ist Deltay der Höhenzuwachs bei einer Windung der Schraubenlinie.

Der Zylinderradius ist r. Weiter ist p die sogenannte reduzierte Ganghöhe der Schraubenlinie. Wird die reduzierte Ganghöhe p mit 2π multipliziert, ergibt sich Deltay.

Kappa ist die Krümmung der Schraubenlinie und tau die Torsion (Windung).

2 Beispiel 2

Das zweite Beispiel ist weniger steil.

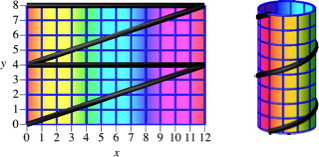
Abb. 2: Beispiel 2

Es ist:

3 Allgemein

Herleitung siehe hier.

Es ist:

Steigung := Deltay/Deltax;

SteigunginProzent := 100*Deltay/Deltax;

SteigungswinkelinGrad := arctan(Steigung)/Pi*180;

Weiter:

r := Deltax/2/Pi;

p := Deltay/2/Pi;

Daraus ergibt sich für die Schraubenlinie die Parameterdarstellung:

[r*cos(t), r*sin(t), p*t], t = 0 .. 2*Pi*Hoehe/Deltay

Die Krümmung kappa und die Torsion tau ergeben sich mit den Formeln:

kappa := r/(r^2 + p^2);

tau := p/(r^2 + p^2);

Websites

Hans Walser: Geometrie

https://www.research-collection.ethz.ch/bitstream/handle/20.500.11850/146667/eth-25629-12.pdf