Hans Walser, [20150705]
Schraubenlinien
Anregung: : J. M. und J. D., H.
1 Die klassische Schraubenlinie
Die Abbildung 0 zeigt eine Schraubenlinie. Es handelt sich um eine Linksschraube.
Abb. 0: Gartenschlauch
Die Abbildung 1a zeigt die klassische Schraubenlinie. In der Abbildung 1b ist die grŸne Schraubenlinie als Achse einer verbogenen blauen Schraubenlinie verwendet worden. In der Abbildung 1c wurde noch eine dritte Generation umgewickelt.
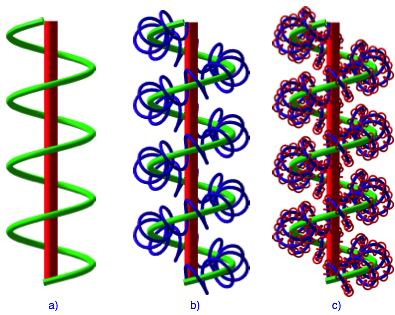
Abb. 1: Schraubenlinien
Alle gezeichneten Schraubenlinien sind Rechtsschrauben.
Wir kšnnen nun die gerade rote Achse ebenfalls verbiegen.
2 Rotoiden
Wir verbiegen die Achse zu einem Kreis (Abb. 2). Genau genommen ist die Achse ein so genannter Torus (Autoschlauch), da wir mit Schlauchgrafik arbeiten.
Abb. 2: Torus
Die Abbildung 3 zeigt nun eine darum gewickelte Schraubenlinie. Diese Figur wird auch als Rotoide bezeichnet.
Abb. 3: Rotoide
In der Abbildung 4 ist eine weitere Schraubenlinie eingewickelt worden.
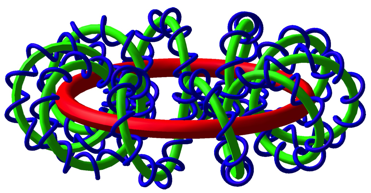
Abb. 4: Rotoidissimo
FŸr meinen Computer war das dann gleich auch das Nonplusultra, weil er eine weitere Generation aus KapazitŠtsgrŸnden nicht mehr schaffte.
3 Parabel
Die Abbildung 5 zeigt die Situation fŸr eine parabelfšrmige Schraubenlinienachse.
Abb. 5: Parabel
Die Abbildung 6 zeigt meinen ersten Versuch.
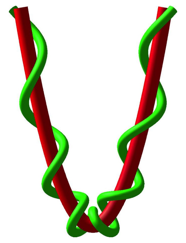
Abb. 6: Mein erster Versuch
Wir
sehen, dass die so genannte Ganghšhe der Schraubenlinie im Parabelscheitel am
kleinsten ist und dann in beiden Richtungen zunimmt. Der Grund ist folgender:
In der Ÿblichen Parabeldarstellung 
ist die
BogenlŠnge der Parabel nicht proportional zum Wachstum von x. Das kann man korrigieren, indem man die Frequenz der grŸnen
Schraubenlinie entsprechend erhšht. Die Frequenz muss mit dem Faktor 
versehen
werden, weil dieser Faktor das Wachstum der BogenlŠnge der Parabel beschreibt.
Durch die Erhšhung der Frequenz wird die PeriodenlŠnge, also die Ganghšhe, entsprechend
reduziert.
Gleichwohl ist die Abbildung 6 Šsthetisch ansprechend.
Bei der Rotoide (Abb. 3) wird der Kreis mit der Ÿblichen Parametrisierung (Kosinus und Sinus) gleichmŠ§ig durchlaufen. Daher ist die Ganghšhe der grŸnen Schraubenlinie konstant.