Hans Walser, [20171223]

Schwalbenschwanz und andere Zinken

1 Worum geht es?

Aus sechs kongruenten Platten soll ein Würfel gebaut werden. Probleme stellen sich bei einer Schwalbenschwanzverzinkung.

2 Mit rechteckigen Platten

Es sei d die Plattendicke. Wir arbeiten mit sechs rechteckigen Platten, deren Breite b um 2d kleiner ist als die Länge a (Abb. 1a). Die Platten setzen wir zu einem Würfel zusammen (Abb. 1b).

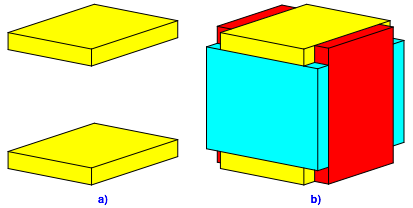
Abb. 1: Rechteckige Platten

An jeder der acht Ecken des Würfels bleibt eine Lücke in Form eines Würfelchens der Kantenlänge d. Da es acht Würfelchens sind, können wir sie nicht regelmäßig auf die sechs Platten verteilen.

Wie steht es mit den Symmetrien der Figur der Abbildung 1b?

3 Verzinkung

Die Platte der Abbildung 2a hat zusätzlich Zinken (Zähne). Beim Würfelmodell fehlen auch hier die acht kleinen Würfelchen an den Ecken.

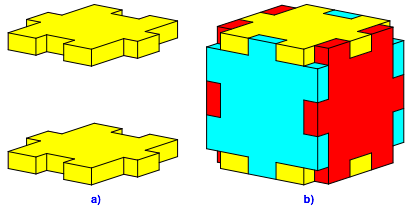
Abb. 2: Verzinkung

4 Schwalbenschwanzverzinkung

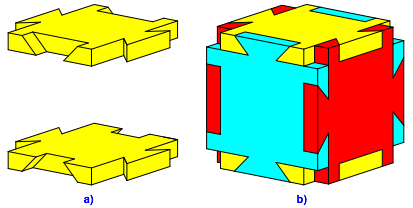
Abb. 3: Schwalbenschwanzverzinkung

Bei der Schwalbenschwanzverzinkung der Abbildung 3 passen die sechs Platten exakt ineinander.

Das Modell hat aber eine Tücke: Wir können die sechs Platten nicht ineinanderpassen. Wir können sogar nicht einmal eine Ecke aus drei Platten bilden. Zwar können wir problemlos zum Beispiel die hellblaue und die rote Platte zusammenfügen (Abb. 4b). Dann aber ist es nicht mehr möglich, die gelbe dritte Platte (Abb. 4a) einzufügen.

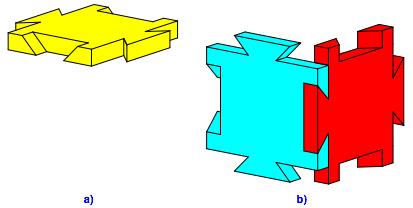
Abb. 4: Die dritte Platte geht nicht hinein

5 Variante zur Schwalbenschwanzverzinkung

Die Abbildung 5 zeigt eine Variante zur Schwalbenschwanzverbindung.

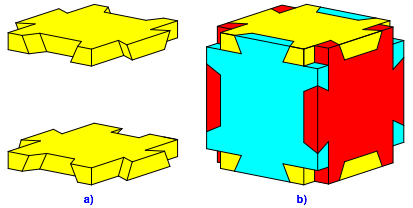
Abb. 5: Schwalbenschwanz, Variante

Wiederum ist es nicht möglich, zuerst zwei Platten zusammenzufügen und anschließend die dritte einzufügen (Abb. 6).

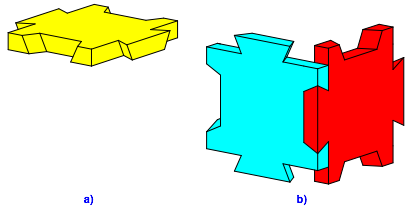
Abb. 6: Versuch, eine Ecke zu bilden

Hingegen funktioniert es, wenn wir die drei Platten simultan zusammenfügen. Dazu starten wir in der Position der Abbildung 7 und schieben dann die drei Platten gleichzeitig nach innen. Man braucht drei Hände dazu.

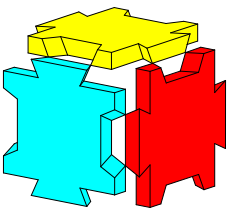
Abb. 7: Start

Die Abbildung 8 zeigt eine Zwischenposition auf halbem Wege.

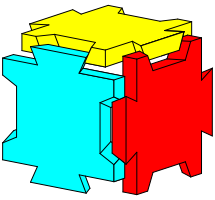
Abb. 8: Zwischenposition

Entsprechend müssen wir für den Zusammenbau aller sechs Platten vorgehen und diese simultan einschieben.

6 Auf Gehrung

Um das Problem der acht fehlenden kleinen Würfelchen an den Würfelecken zu lösen, müssen wir auf Gehrung arbeiten. Die einzelnen Platten sind je ein Pyramidenstumpf (Abb. 9). Die Pyramidenspitze ist der Mittelpunkt des zukünftigen Würfels.

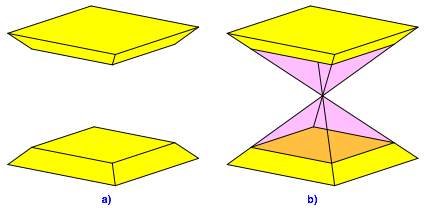
Abb. 9: Pyramidenstumpf

Der Neigungswinkel der Seitenflächen der Pyramide gegenüber der Grundebene ist 45°. Der Winkel zwischen zwei Seitenflächen der Pyramide ist 120°. Dies kann mit der Sicht über eine Seitenkante eingesehen werden (Abb. 10).

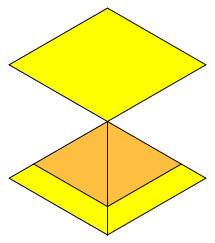
Abb. 10: Spezielle Sicht

Die Abbildung 11a zeigt eine Eckkonfiguration mit drei Seitenplatten, die Abbildung 11b den Würfel.

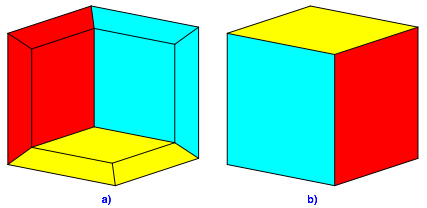
Abb. 11: Auf Gehrung

7 Kombination

Die Abbildung 11a zeigt eine Kombination der Rechteckplatten (Abb. 1) mit den auf Gehrung zugeschnittenen Platten (Abb. 9). Den Rechteckplatten sind seitlich kleine Pyramiden angesetzt gemäß Abbildung 13.

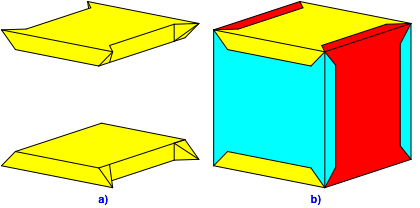
Abb. 12: Kombination

Diese kleinen Pyramiden haben eine quadratische Grundfläche, welche in der Abbildung 13b senkrecht sichtbar ist. Die Spitze ist nicht über der Mitte der Grundfläche, sondern über einer Ecke. Die Pyramide passt in ein kleines Würfelchen. Ihr Volumen ist ein Drittel des Volumens des Würfelchens.

Abb. 13: Kleine Pyramiden

Nun können wir eine Kontrollrechnung machen. Pro Platte haben wir vier Drittel des Würfelchenvolumens angefügt. Auf alle sechs Platten sind das 24 Drittel, also acht Würfelchenvolumina. Das sind genau die acht Würfelchen, welche in den Ecken der Abbildung 1b fehlen.