Hans Walser, [20100417a]
Schwerpunkt beim Dreieck
Zwei Eigenschaften im Zusammenhang mit dem Schwerpunkt des Dreieckes.
1 Aufsetzen Šhnlicher Dreiecke
1.1
Allgemeiner Fall
Einem beliebigen
Dreieck 
setzen wir auf
den Seiten drei zueinander Šhnliche Dreiecke 
, 
und 
an. Die Dreiecke
dźrfen nach au§en oder nach innen angesetzt werden.
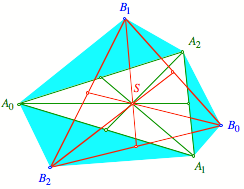
Ansetzen Šhnlicher
Dreiecke
Dann haben die beiden
Dreiecke 
und 
denselben
Schwerpunkt S.
Beweis
Wir interpretieren die
Punkte als komplexe Zahlen in der Gau§schen Zahlenebene. ZunŠchst ist dann:
Weiter gilt wegen der
€hnlichkeit der angesetzten Dreiecke:
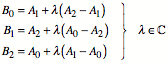
Fźr den Schwerpunkt T des Dreieckes 
erhalten wir:
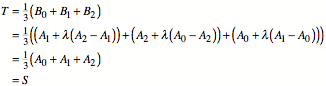
1.2
Verallgemeinerung
Der Sachverhalte und
die Beweisfźhrung lassen sich auf ein beliebiges n-Eck 
und seinen
Eckenschwerpunkt S verallgemeinern.
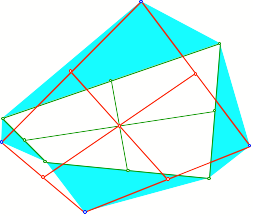
Situation im Viereck
1.3
Sonderfall: Napoleon-Barlotti
Wir setzen einem
beliebigen Dreieck 
gleichseitige
Dreiecke auf und bezeichnen deren Mittelpunkt mit 
. GemŠ§ dem Satz von Napoleon-Barlotti ist das Dreieck 
gleichseitig.
Sein Mittelpunkt ist der Schwerpunkt des Dreieckes 
. In diesem Sonderfall ist 
(vgl: [Coxeter/Greitzer
1983], S. 67f, S. 167f).
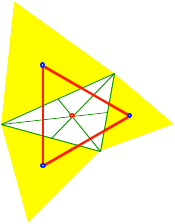
Sonderfall
2
Schwerpunkt als Drehzentrum
Wir beginnen mit dem
beliebigen Dreieck 
mit dem
Schwerpunkt S. Wir drehen den Punkt 
um S um den Winkel 
und erhalten so
den Punkt 
.
Dann ist das Dreieck 
gleichseitig.
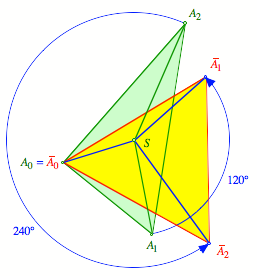
Ein gleichseitiges
Dreieck entsteht
Beweis
Wir arbeiten wieder in
der Gau§schen Zahlenebene und setzen den Ursprung in den Schwerpunkt S. Dann ist zunŠchst 
. Weiter ist
Zu prźfen ist:
Einsetzen ergibt:
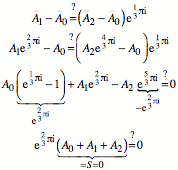
Der Sachverhalt lŠsst
sich nicht auf n-Ecke verallgemeinern.
Literatur
[Coxeter/Greitzer 1983] Coxeter,
H. S. M. / Greitzer, S. L.: Zeitlose Geometrie. Stuttgart: Klett 1983. ISBN
3-12-983390-0