Hans Walser, [20240605]

Schwerpunkt

Anregung: Peter Gallin, Zürich

1 Worum es geht

Alternative Methoden zur Konstruktion des Schwerpunktes eines Dreieckes.

Mit DGS verifiziert. Der Autor ist dankbar um formale Beweise.

2 Quadrate ansetzen

Den drei Seiten eines beliebigen Dreiecks setzen wir Quadrate an (Abb. 1). Die Dreiecksecken werden grün, die Außenecken der Quadrate im Wechsel blau und rot markiert.

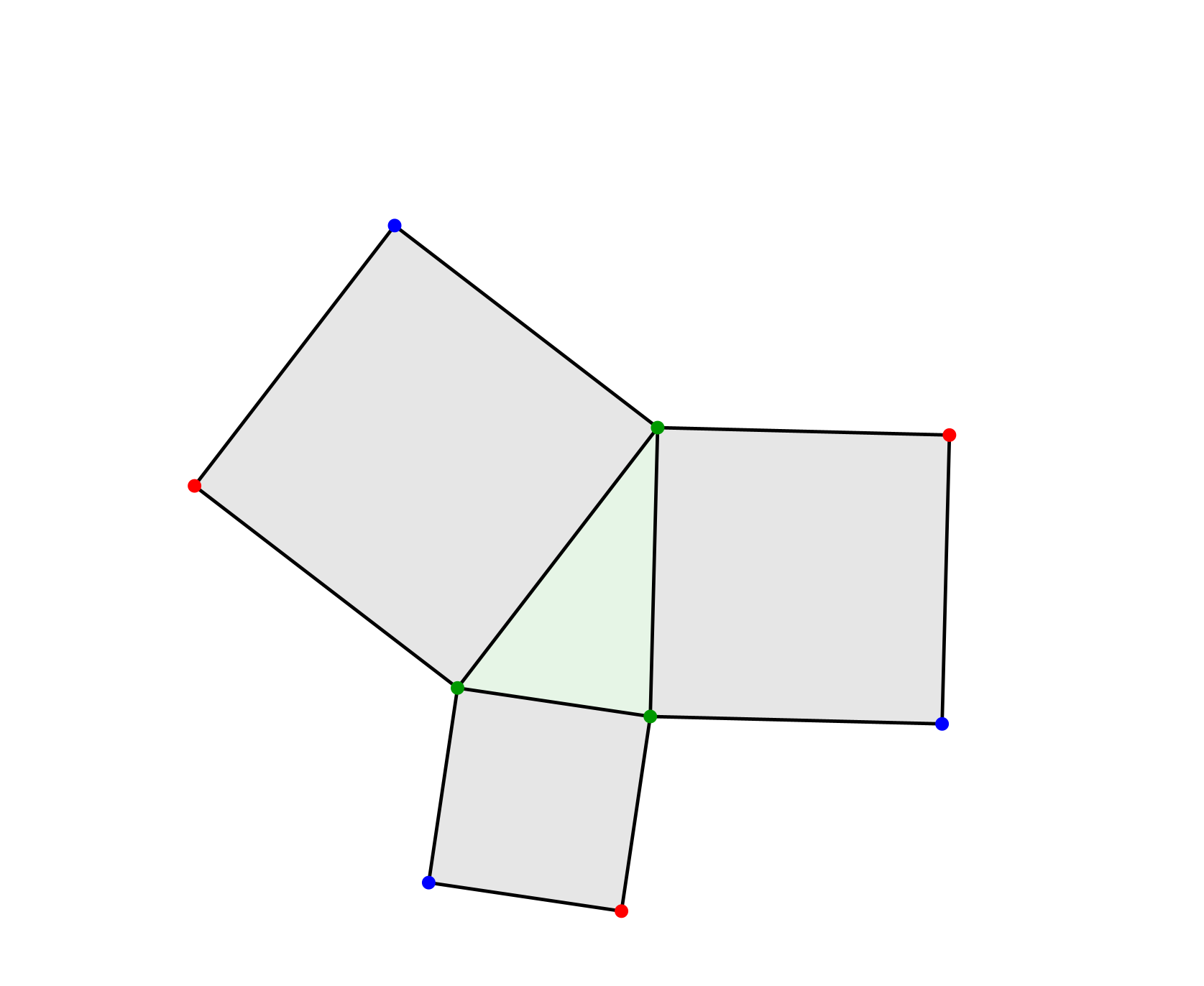
Abb. 1: Quadrate ansetzen

3 Dreiecke

Die blauen Eckpunkte definieren ein Dreieck (Abb. 2).

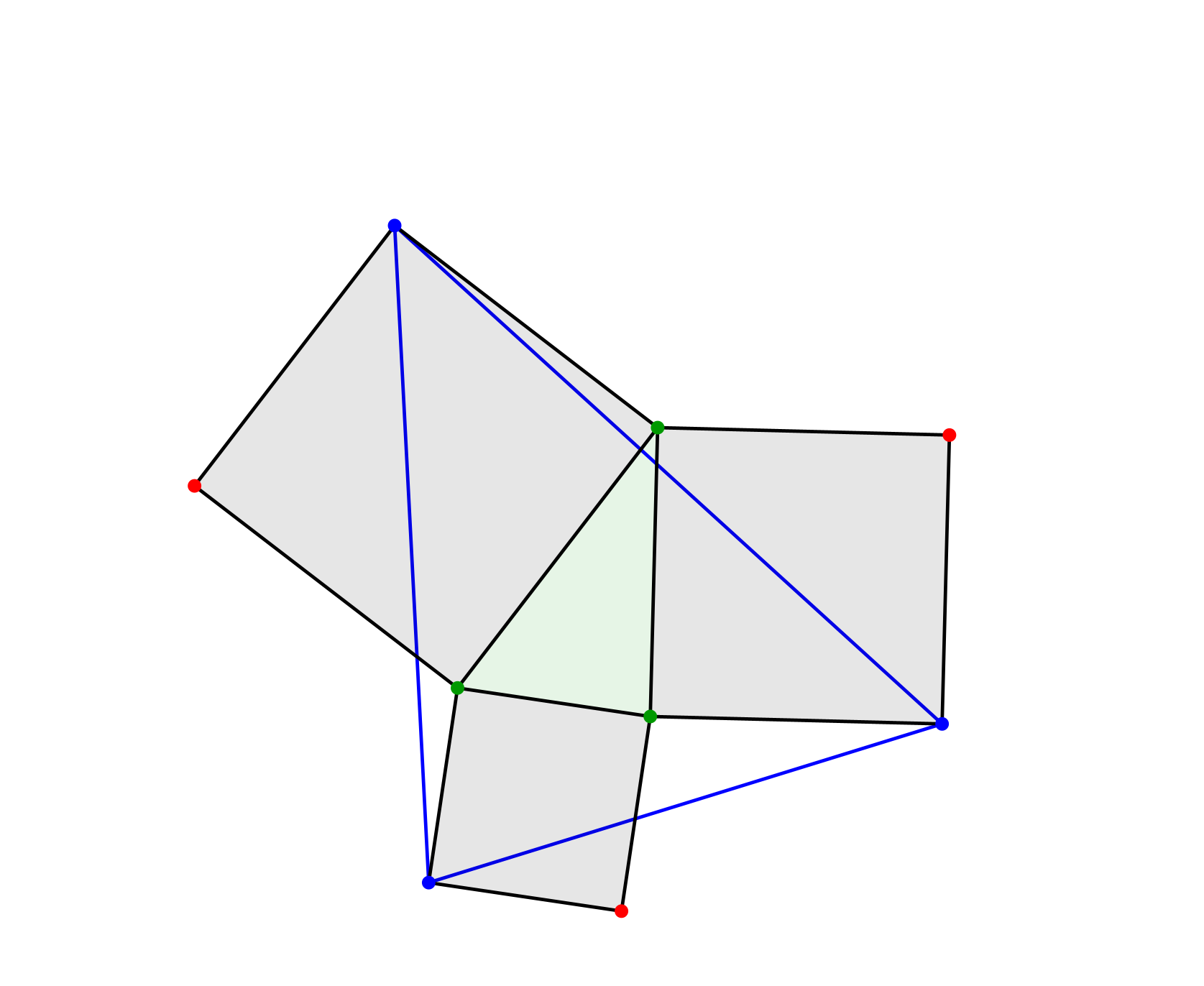
Abb. 2: Blaues Dreieck

Analog definieren die roten Eckpunkte ein Dreieck (Abb. 3). Die beiden Dreiecke haben sechs Schnittpunkte, welche wir im Wechsel magenta und lila markieren.

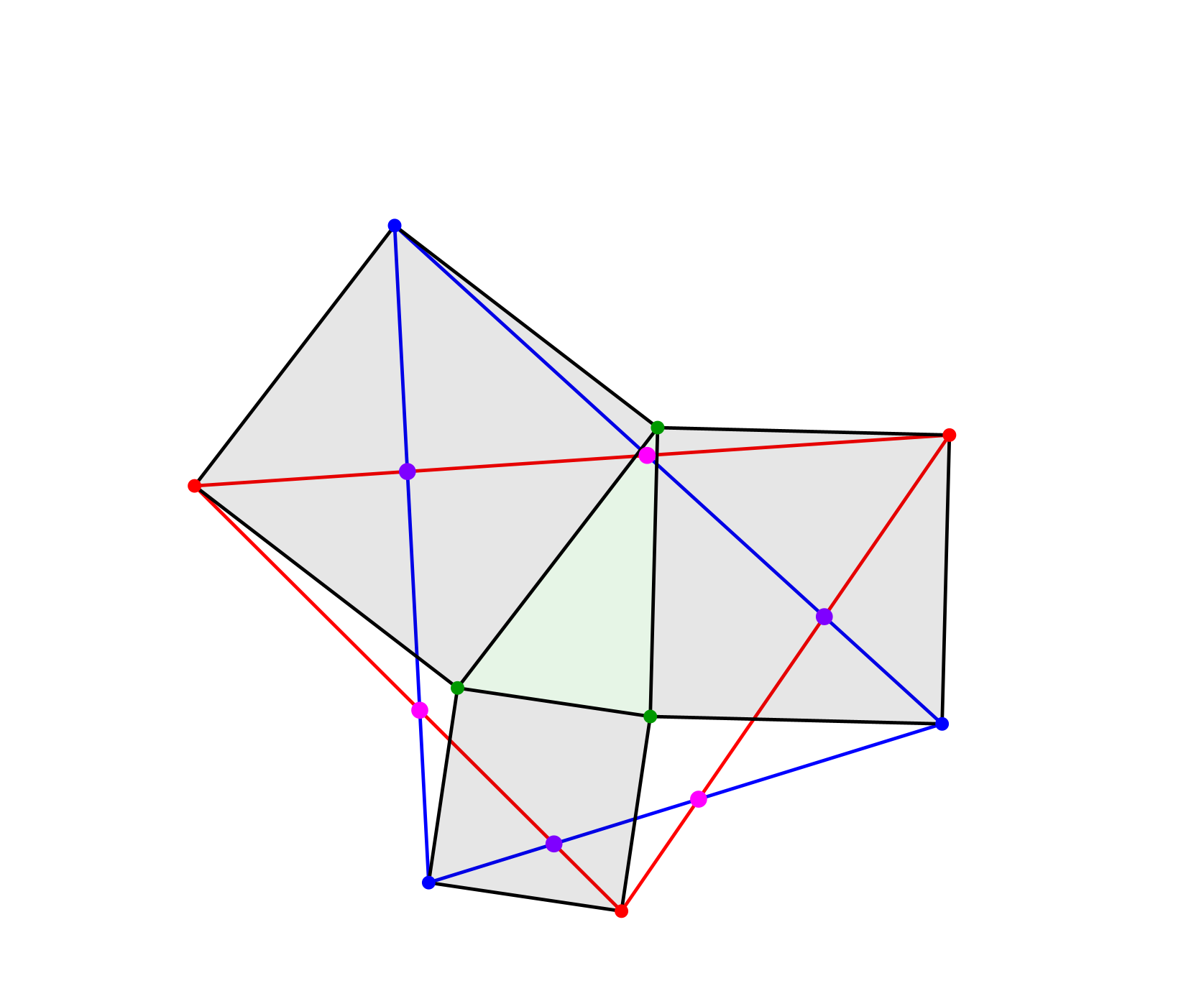
Abb. 3: Rotes Dreieck

Bemerkung: Man kann zeigen, dass das blaue und das roten Dreieck denselben Flächeninhalt haben. Die beiden Dreiecke sind aber in der Regel nicht kongruent.

4 Schwerpunkt

Es zeigt sich, dass wir sowohl mit den magenta Schnittpunkten wie mit den lila Schnittpunkten den Schwerpunkt konstruieren können.

4.1 Magenta Schnittpunkte

Die drei Geraden durch die magenta Punkte und die naheliegenden grünen Dreiecksecken haben einen gemeinsamen Schnittpunkt (Abb. 4). Dieser ist der Schwerpunkt.

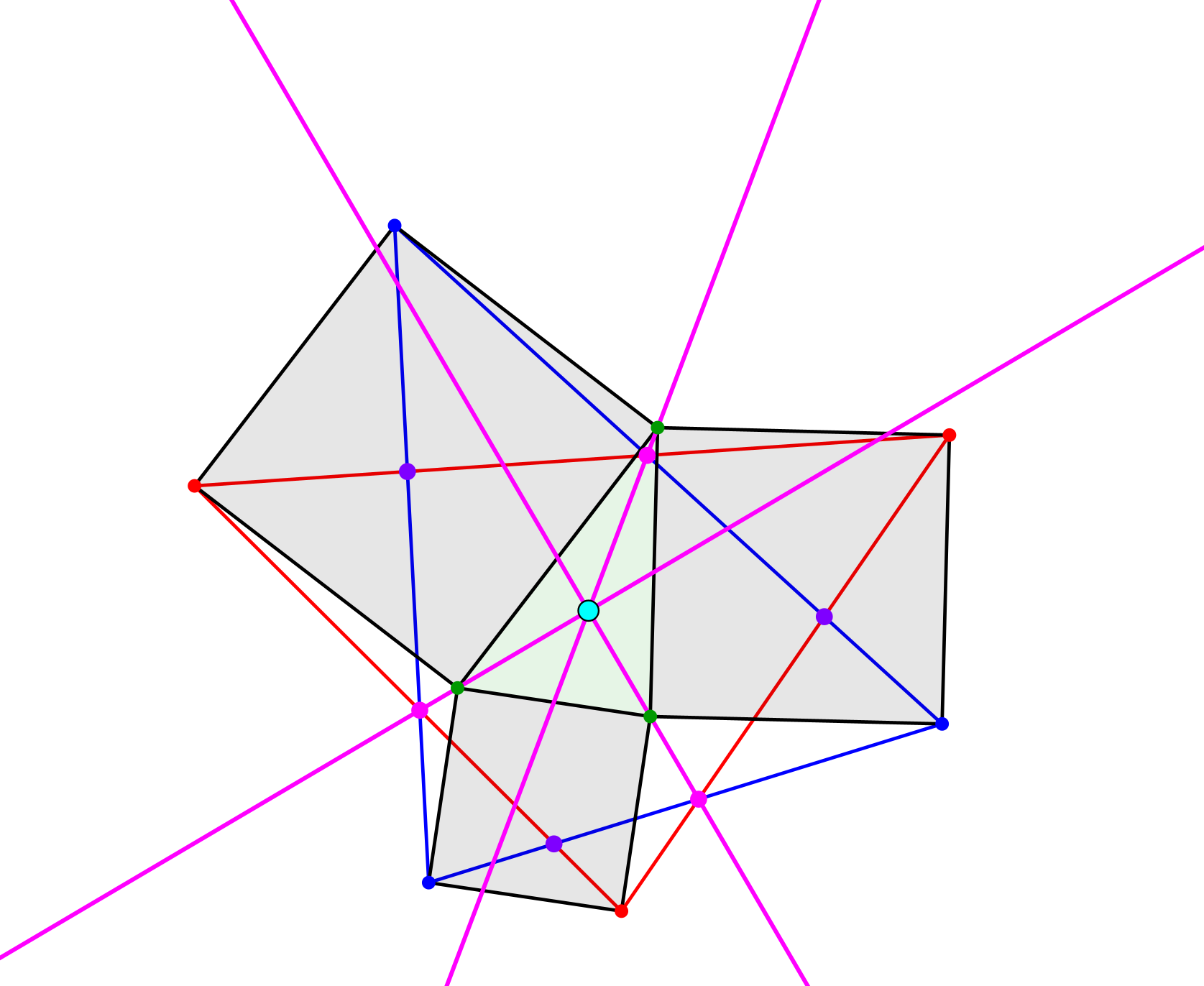
Abb. 4: Schwerpunkt

Die magenta Linien sind natürlich die Schwerlinien des Startdreieckes. Das „Alternative“ in dieser Konstruktion besteht darin, dass diese Schwerlinien nicht in der üblichen Weise mit den Seitenmitten konstruiert werden.

Man kann zeigen, dass der Schwerpunkt des Startdreieckes ist auch der Schwerpunkt des blauen und des roten Dreiecks ist.

4.1.1 Ähnliche Rechtecke

Die Konstruktion funktioniert auch noch, wenn die Quadrate durch ähnliche Rechtecke ersetzt werden (Abb. 5). Der Parameter k ist das Seitenverhältnis der Rechtecke.

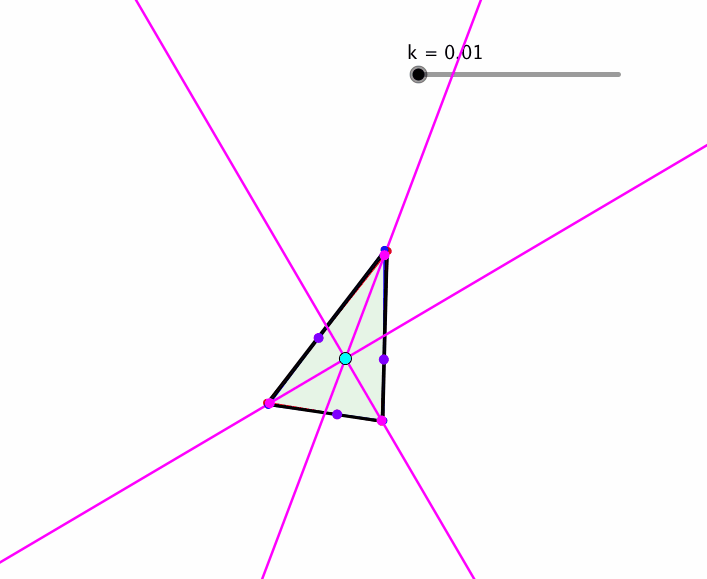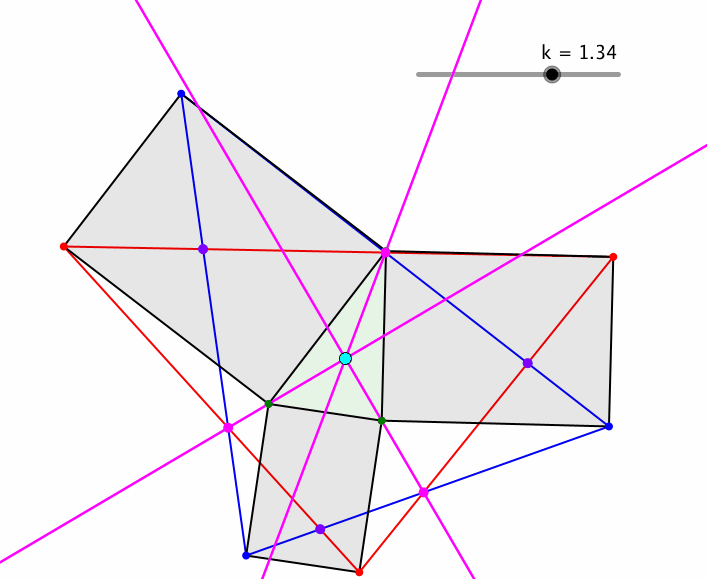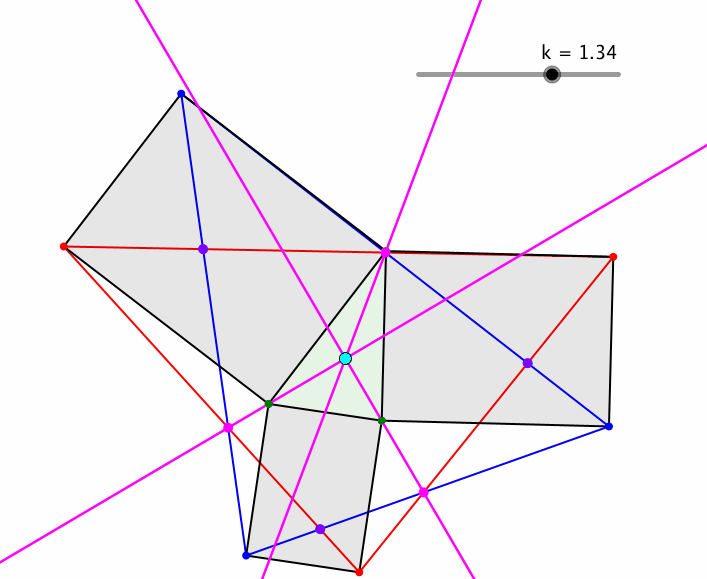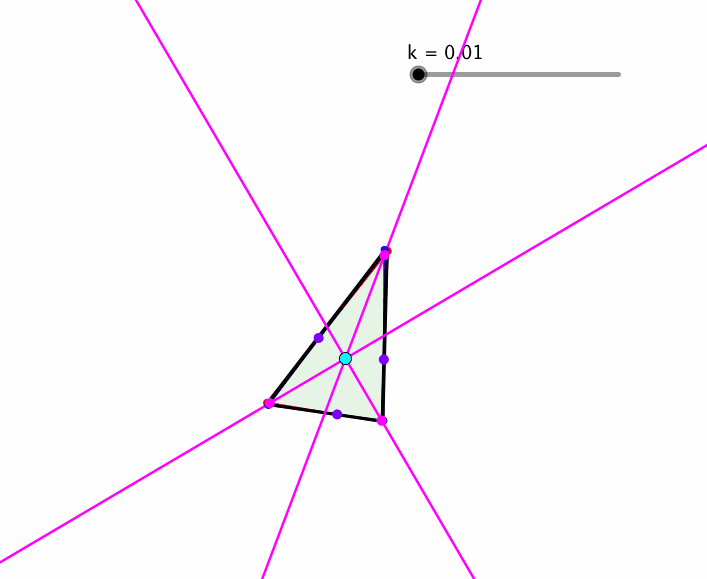
Abb. 5: Ähnliche Rechtecke

4.1.2 Ähnliche Trapeze

Die Rechtecke können sogar durch ähnliche gleichschenklige Trapeze ersetzt werden (Abb. 6). Dabei sind k das Verhältnis der Schrägseiten zur Basisparallelen und ϕ der Basiswinkel.

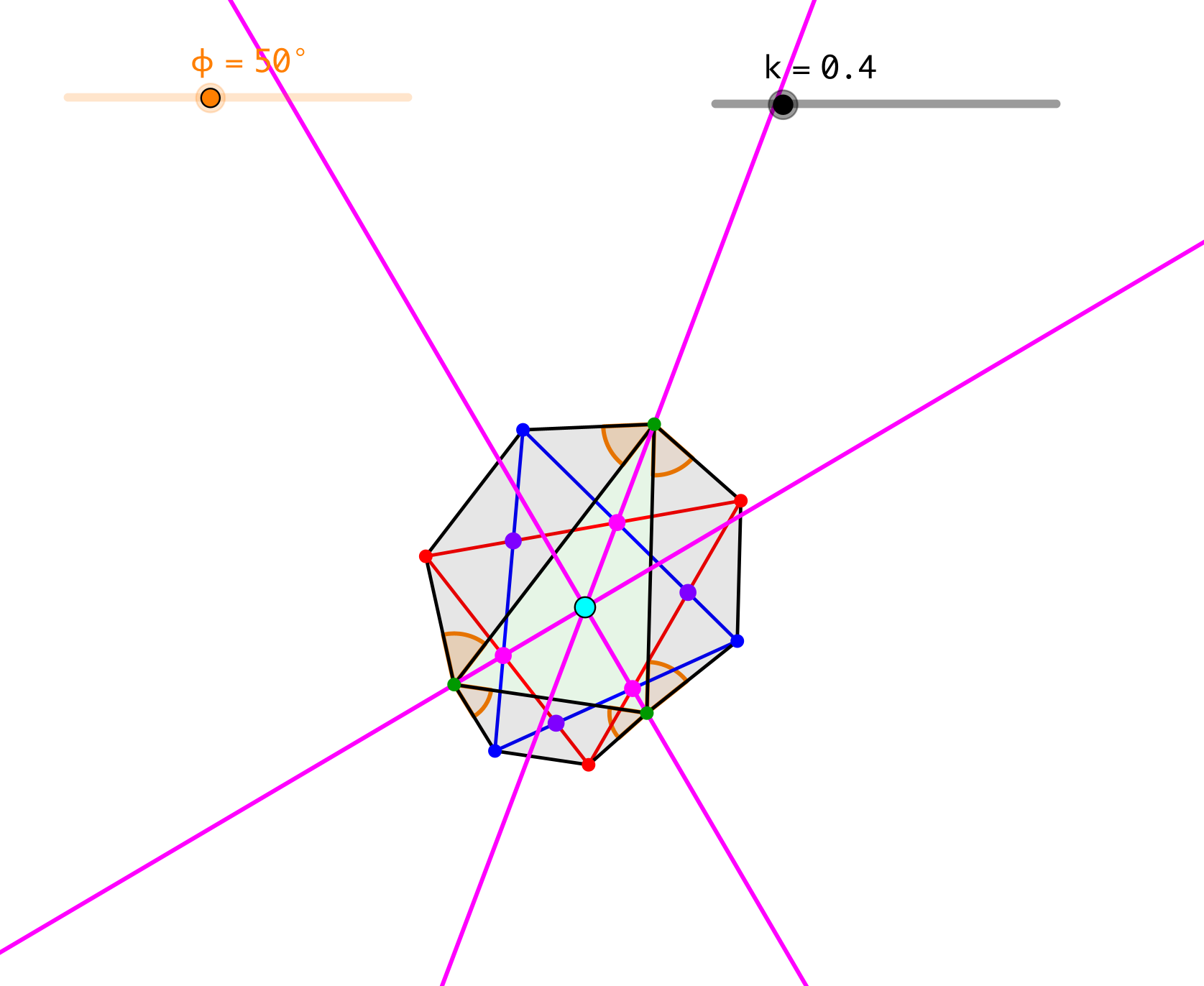
Abb. 6: Ähnliche gleichschenklige Trapeze

Für die Animation haben wir nun zwei Parameter, nämlich k und ϕ.

Variation von k (Abb. 7) führt zu „überschlagenen“ Trapezen.

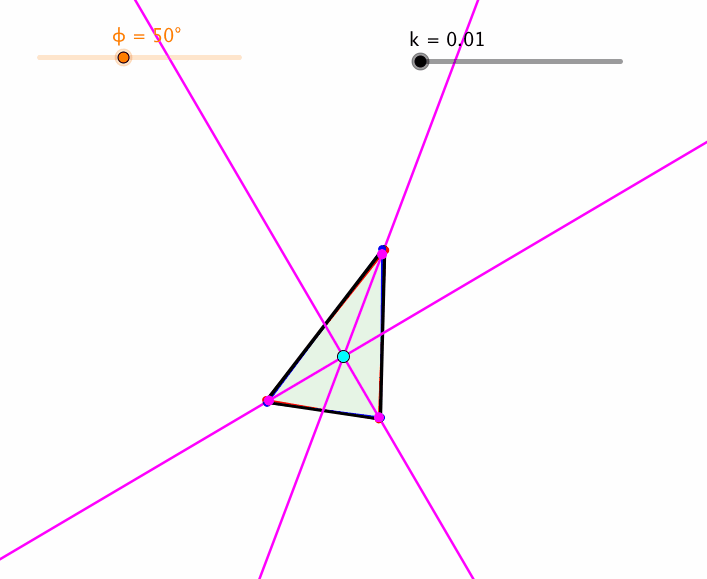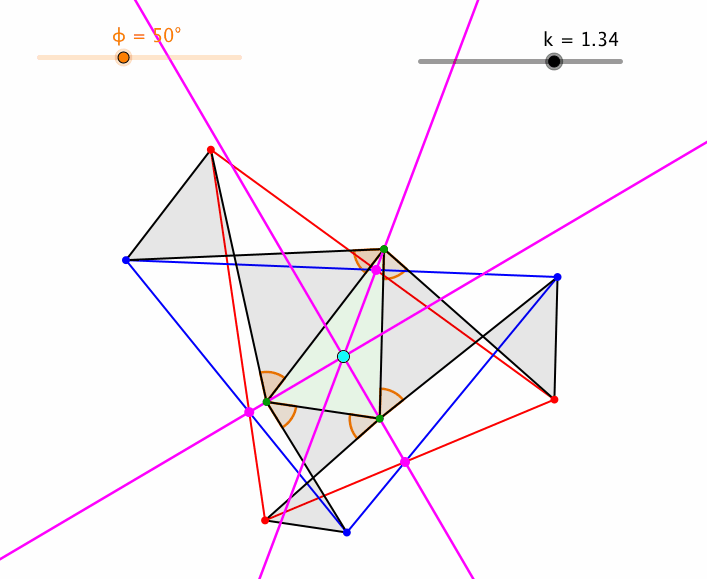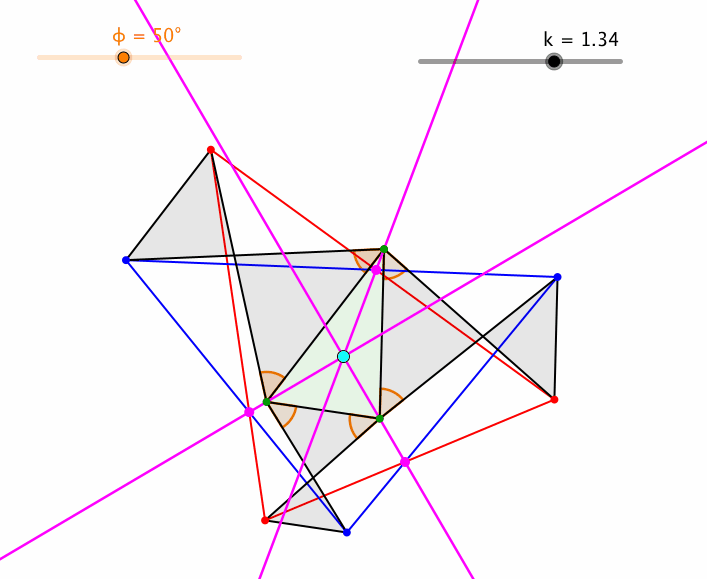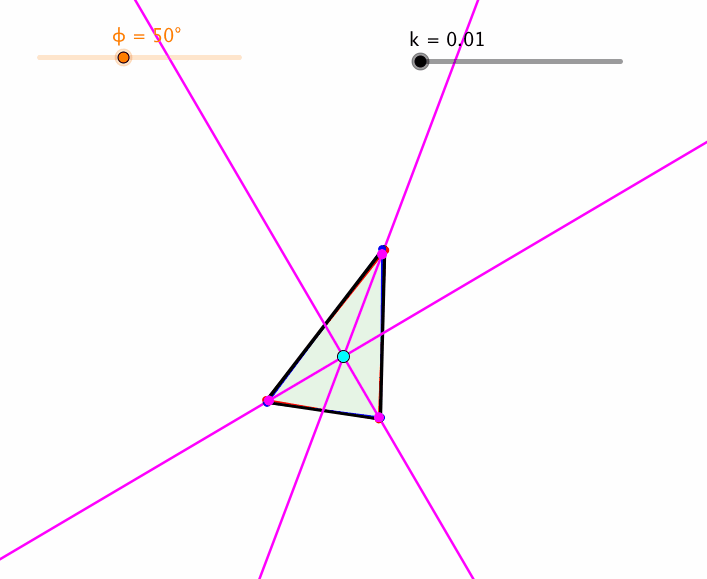
Abb. 7: Variation von k

Auch der Basiswinkel ϕ kann variiert werden (Abb. 8).

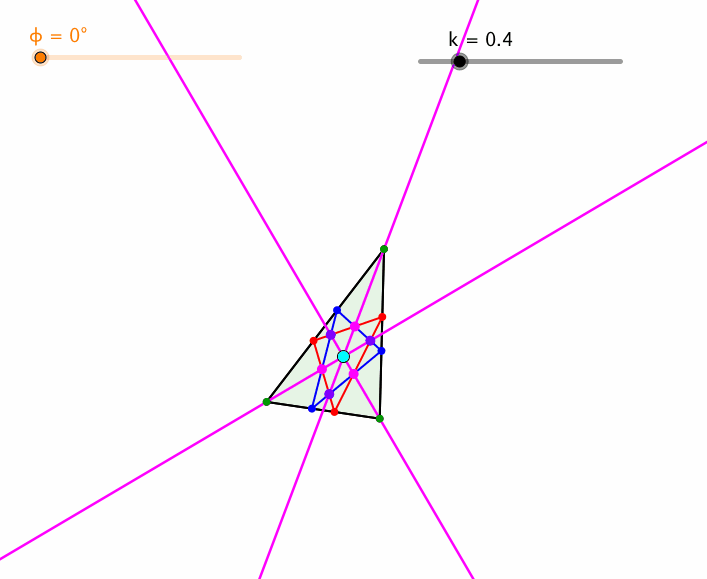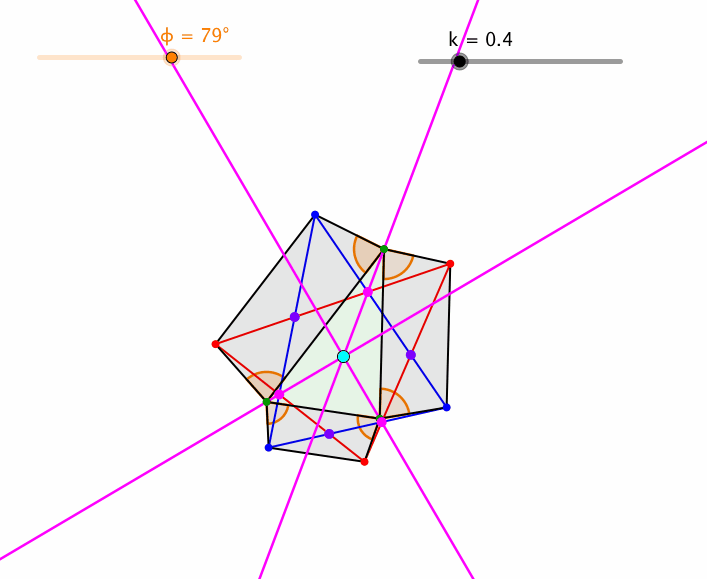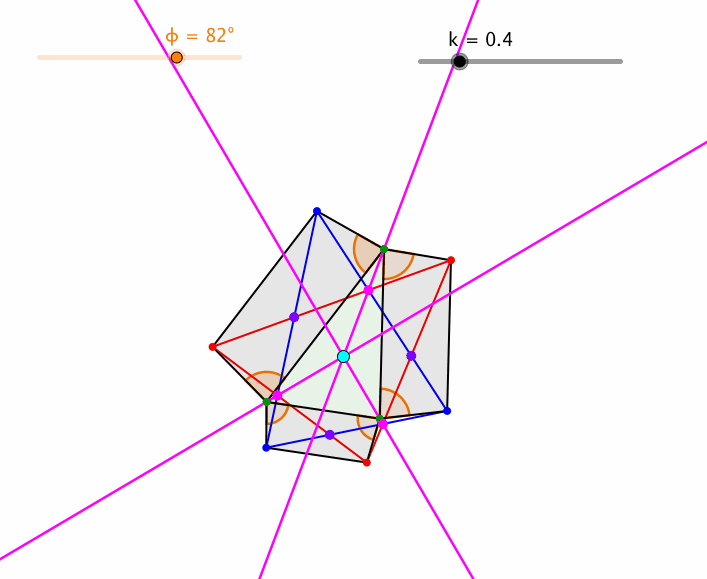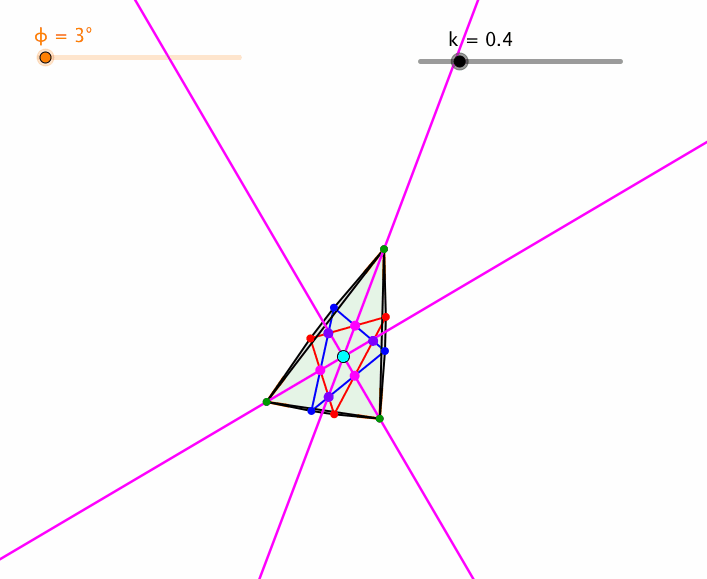
Abb. 8: Variation von ϕ

In der Abbildung 9 variieren k und ϕ beide proportional zur Zeit.

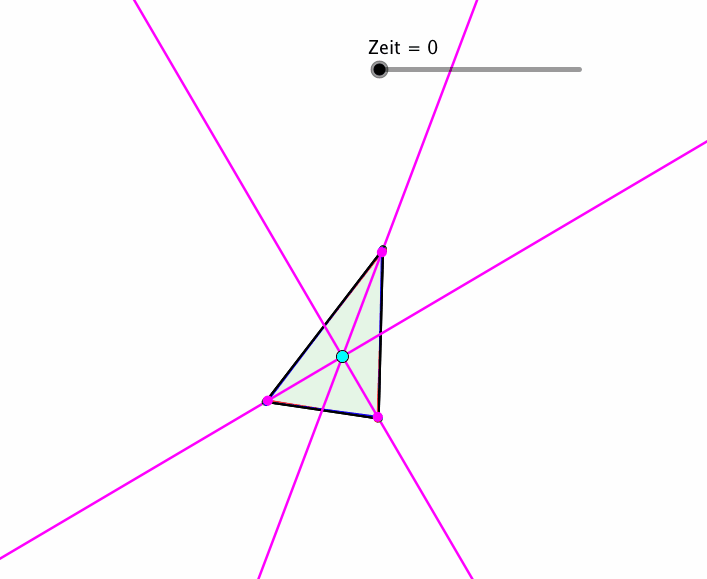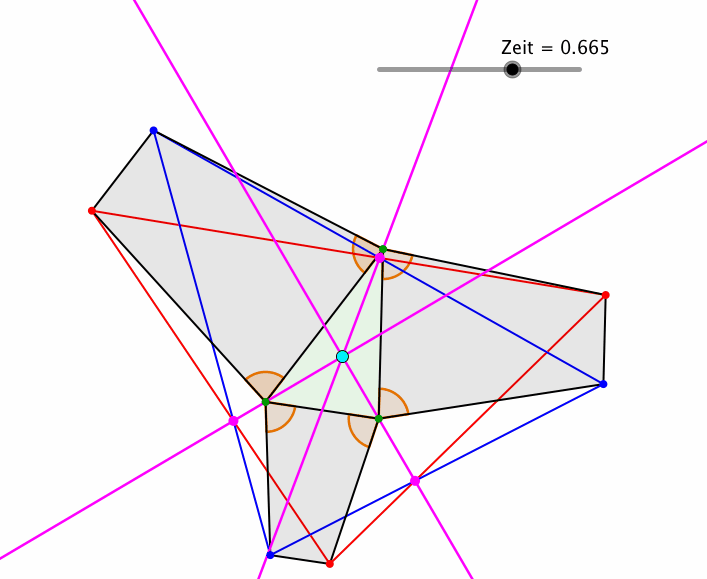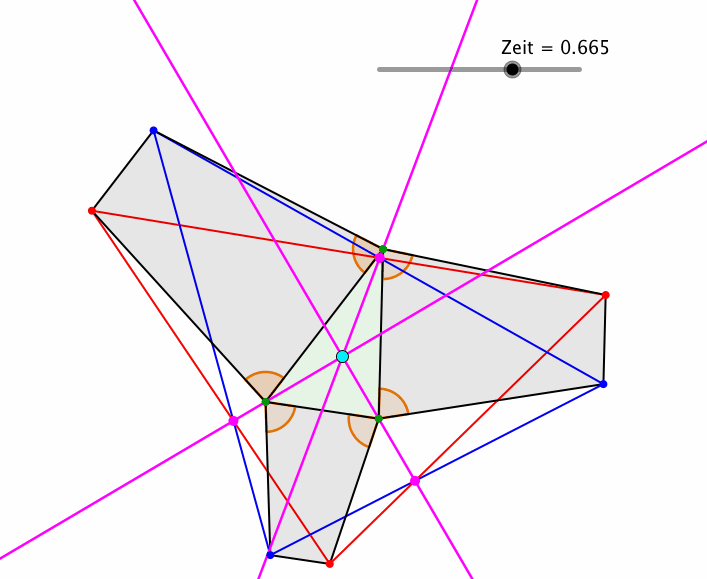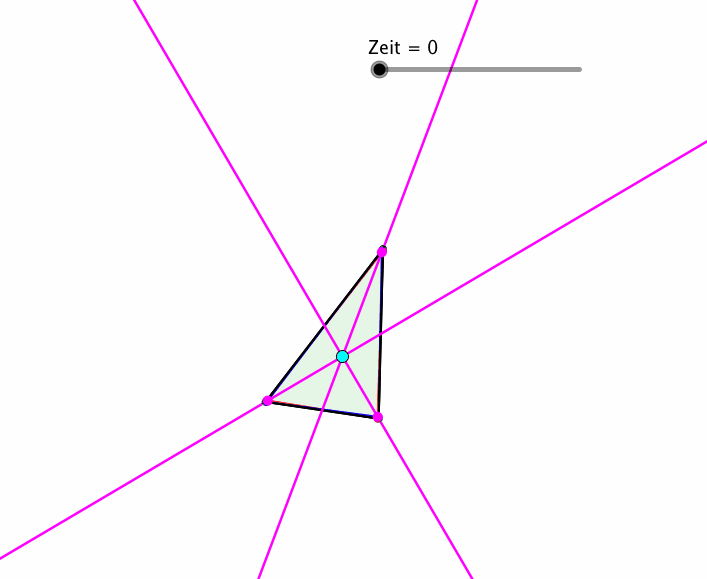
Abb. 9: Es eilt die Zeit

4.2 Lila Schnittpunkte

Von den lila Schnittpunkten aus fällen wir die Lote auf die naheliegende Seite des Startdreiecks (Abb. 10). Die drei Lote schneiden sich in einem Punkt. Dieser ist der Schwerpunkt.

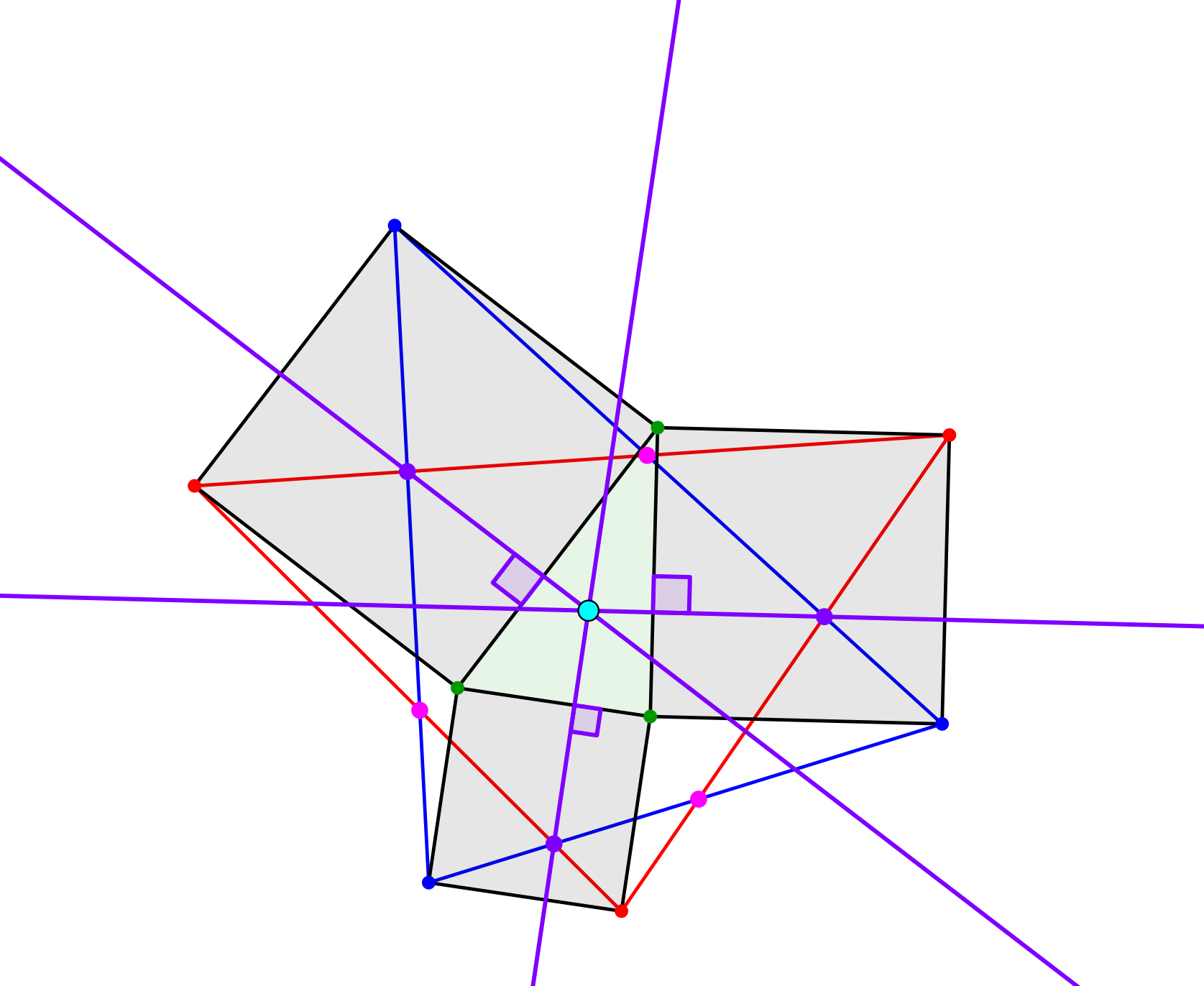
Abb. 10: Lote auf die Dreiecksseiten

Die Quadrate können wiederum durch ähnliche Rechtecke ersetzt werden (Abb. 11).

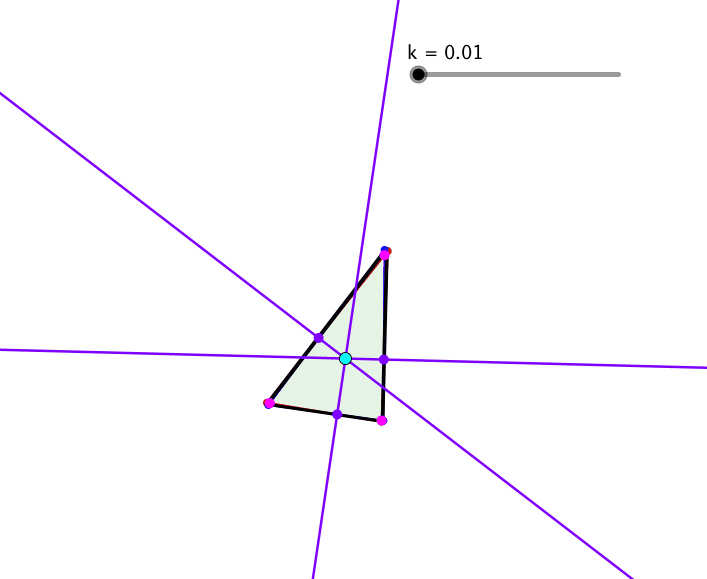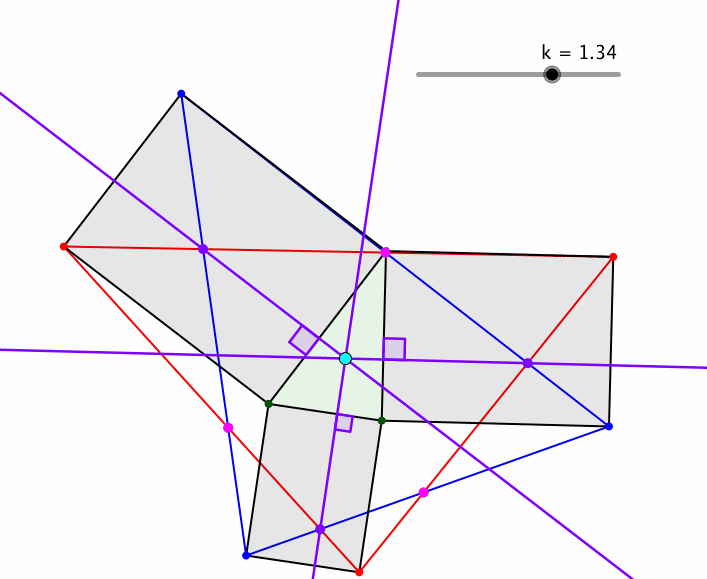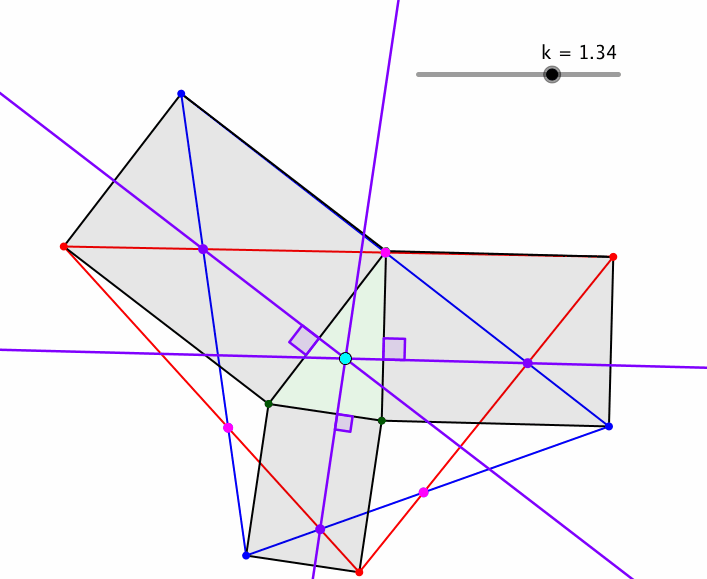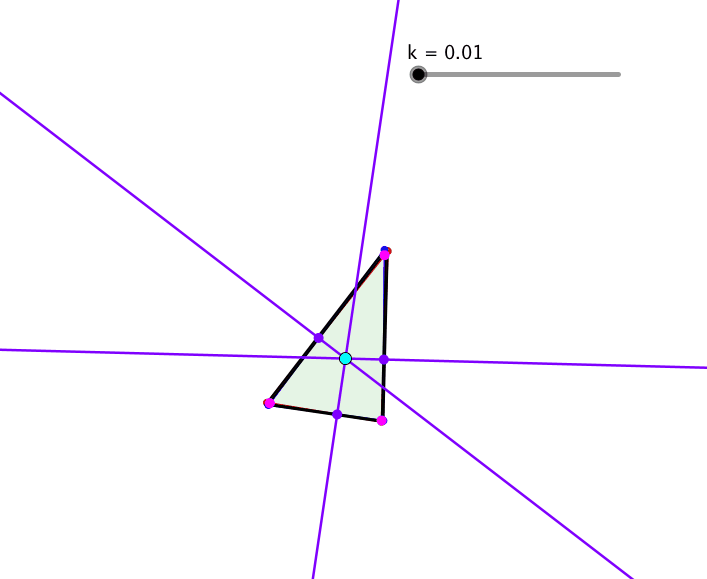
Abb. 11: Ähnliche Rechtecke

Leider funktioniert es nicht mehr mit ähnlichen gleichschenkligen Trapezen. Die Abbildung 12 zeigt ein Gegenbeispiel.

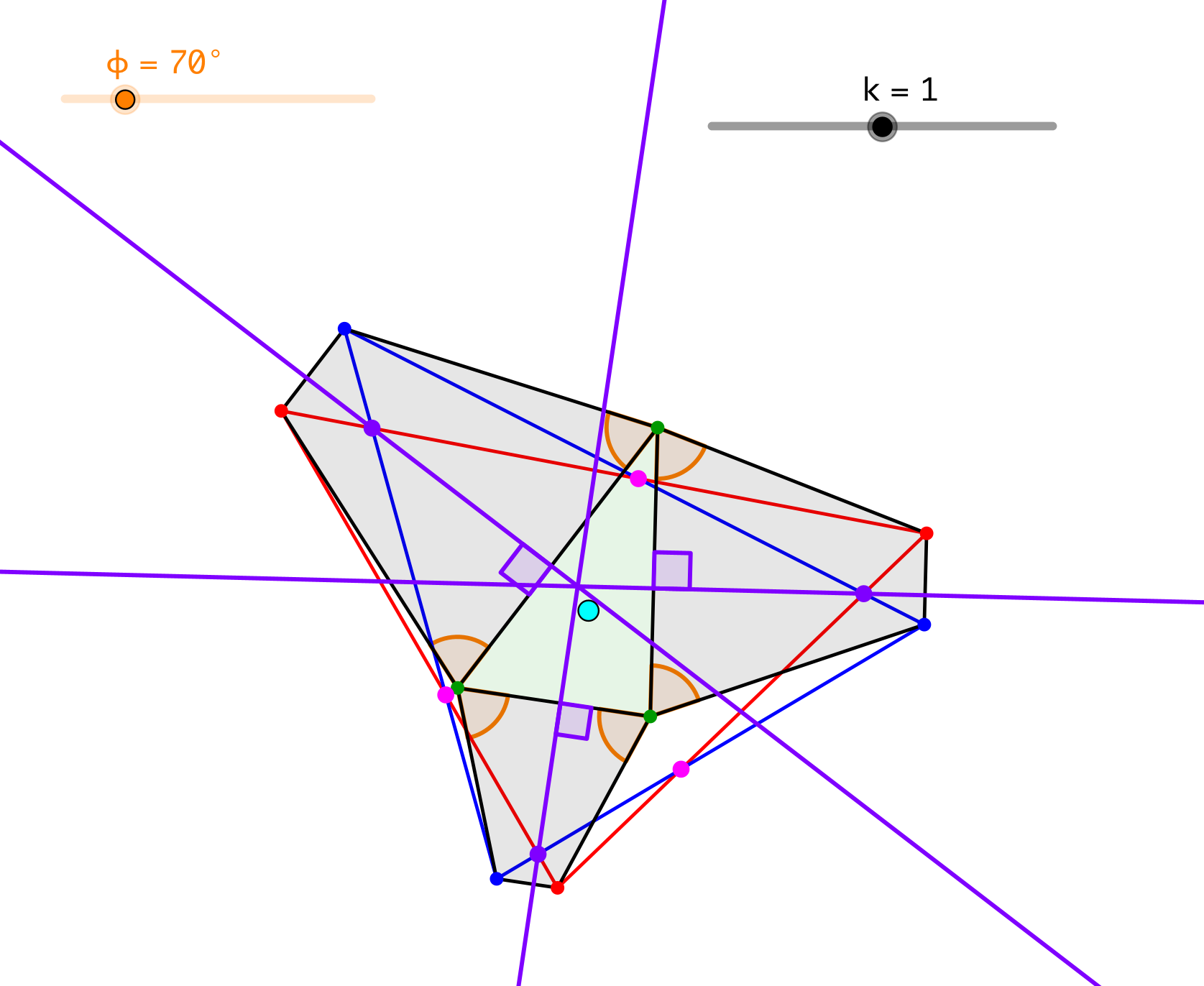
Abb. 12: Gegenbeispiel

Es ist sogar so, dass sich die drei Lote nicht in einem gemeinsamen Punkt schneiden. Die Abbildung 13 zeigt die Situation in 40-facher Vergrößerung. Es ist bereits erkennbar, dass die drei Lote keinen gemeinsamen Schnittpunkt haben.

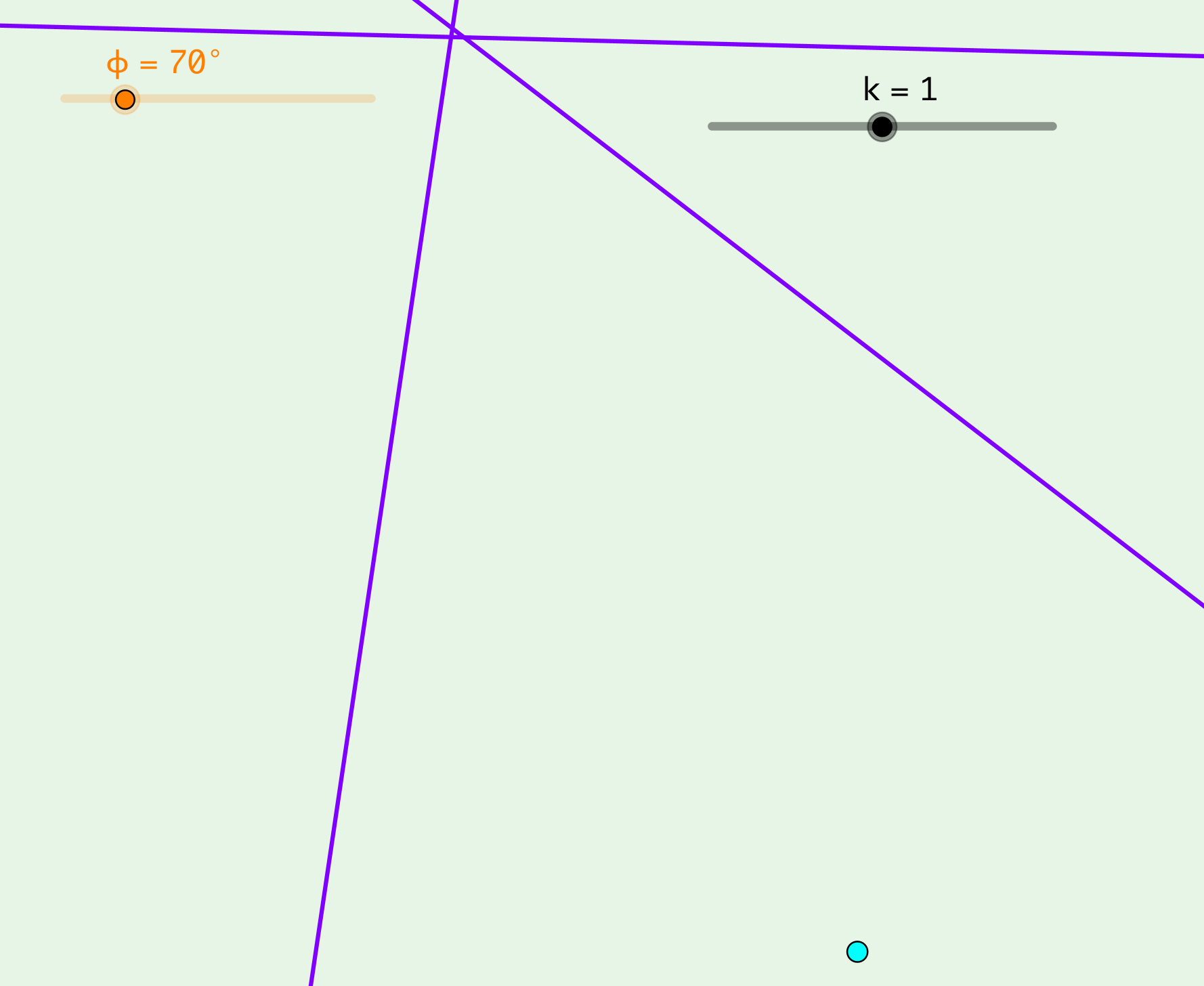
Abb. 13: Hineinzoomen