1 Worum geht es?

Auf der Basis eines regelmäßigen Sechsecks wird eine eckige logarithmische Spirale konstruiert.

2 Sechsecke ansetzen

Wir beginnen mit einem regelmäßigen Sechseck (Abb. 1).

Abb. 1: Startsechseck

Dem Sechseck fügen wir übereck ein zweites Sechseck an, das noch mit dem Faktor f gestreckt wird (Abb. 2 für f = 0.8, die Streckung ist also für Normalverbraucher eine „Schrumpfung“).

Abb. 2: Sechseck anfügen

Diesem Sechseck fügen wir entsprechend ein weiteres Sechseck an (Abb. 3).

Abb. 3: Weiteres Sechseck anfügen

Wenn wir entsprechend weiterfahren, erkennen wir, worauf es hinauswill (Abb. 4).

Abb. 4: Viertes Sechseck

3 Spirale

Durch Iteration entsteht eine Spirale (Abb. 5).

Abb. 5: Spirale

4 Variation des Streckfaktors

Für den Streckfaktor f = 0.9 ergibt sich eine Spirale mit Selbstüberlappung (Abb. 6).

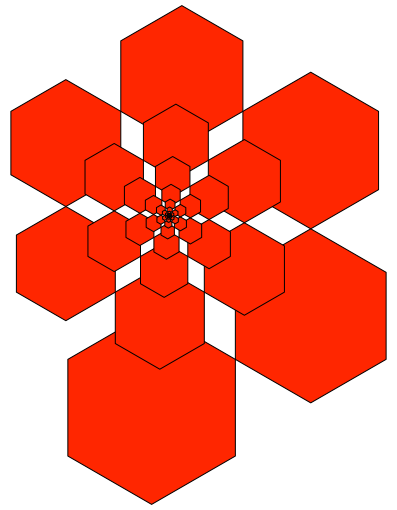
Abb. 6: Selbstüberlappung

Die Abbildung 7 zeigt Werden und Vergehen dieser Spirale.

Abb. 7: Genesis der Spirale

In der Abbildung 8 wird der Streckfaktor f zwischen 0 und 1 variiert. Die jeweiligen Spiralen sind so positioniert, dass das Spiralenzentrum an Ort bleibt. Dies kann mit dem Mauszeiger überprüft werden.

Abb. 8: Variation des Streckfaktors

5 Sonderfälle

Im Beispiel der Abbildung 9 sitzt das siebente Sechseck auf dem ersten.

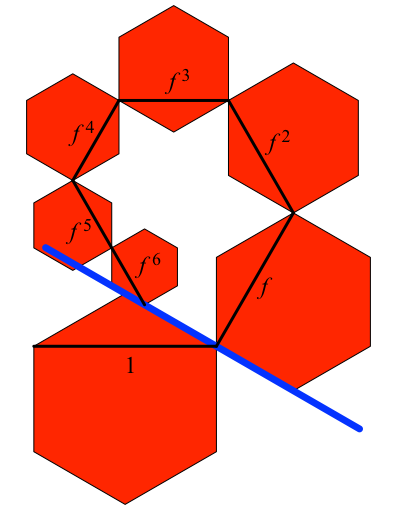
Abb. 9: Berechnung des Sonderfalls

Die mit Maßverhältnissen eingezeichneten schwarzen Linien zeigen, dass für das Aufsitzen die Bedingung erfüllt sein muss (Tipp: Entfernung von der dicken blauen Linie):

Für die von null verschiedene reelle Lösung kann diese Gleichung reduziert werden auf:

Die nun noch einzige reelle Lösung ist numerisch: f ≈ 0.8433484093.

Die Abbildungen 10 und 11 zeigen die Spirale. Es sitzt jedes Sechseck auf dem um sechs Generationen älteren Sechseck.

Abb. 10: Sonderfall

Abb. 11: Sonderfall

Für f = 1 erhalten wir einen von sechs Sechsecken eingerahmten David-Stern (Abb. 12):

Abb. 12: Stern

Weblinks

Hans Walser: Quadratspirale

http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadratspirale2/Quadratspirale2.html

Hans Walser: Sechseckspirale

http://www.walser-h-m.ch/hans/Miniaturen/S/Sechseckspirale/Sechseckspirale.html

Literatur

Walser, Hans (2022): Spiralen, Schraubenlinien und spiralartige Figuren. Mathematische Spielereien in zwei und drei Dimensionen. Springer Spektrum. ISBN 978-3-662-65131-5 und ISBN 978-3-662-65132-2 (eBook).