Hans Walser, [20150130]
Sehnenviereck und Tangentenviereck
1 Worum geht es?
Es werden ZusammenhŠnge zwischen Sehnenviereck und Tangentenviereck untersucht.
2 Gewusst wie
Gewusst wie ist besser als verstanden warum.
2.1 Vom Tangentenviereck zum Sehnenviereck
Zu einem Tangentenviereck zeichnen wir die Šu§eren Winkelhalbierenden. Diese bilden ein Sehnenviereck (Abb. 1).
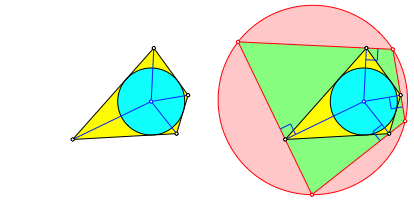
Abb. 1: Vom Tangentenviereck zum Sehnenviereck
2.2 Vom Sehnenviereck zum Tangentenviereck
Vom Diagonalenschnittpunkt eines Sehnenviereckes fŠllen wir die Lote auf die Seiten. Die Lotfu§punkte bilden ein Tangentenviereck (Abb. 2).
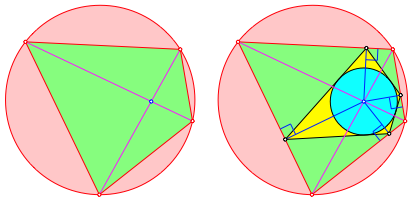
Abb. 2: Vom Sehnenviereck zum Tangentenviereck
3 Verstanden warum
3.1 Vom Tangentenviereck zum Sehnenviereck
Im
Tangentenviereck ABCD fźhren wir
zusŠtzlich die Winkel ![]() und
und ![]() gemŠ§ Abbildung
3 ein.
gemŠ§ Abbildung
3 ein.
Abb. 3: Bezeichnungen
Es ist dann:
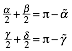
Wegen der Winkelsumme im Viereck ist weiter:
![]()
Durch Subtraktion dieser Gleichung von der Summe der beiden oberen Gleichungen ergibt sich:
![]()
Die
beiden Winkel ![]() und
und ![]() verhalten
sich also wie gegenźberliegende Winkel eines Sehnenviereckes. Daraus folgt die
Stimmigkeit der Konstruktion gemŠ§ Abbildung 1.
verhalten
sich also wie gegenźberliegende Winkel eines Sehnenviereckes. Daraus folgt die
Stimmigkeit der Konstruktion gemŠ§ Abbildung 1.
Verallgemeinerung: Wir kšnnen die vier Šu§eren Winkelhalbierenden gemŠ§ Abbildung 1 je um den gleichen Winkel um die Ecken des Tangentenviereckes verdrehen und erhalten immer noch ein Sehnenviereck (Abb. 4).
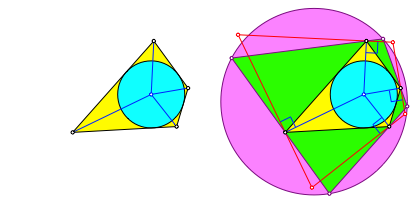
Abb. 4: Weitere Lšsung
Wir haben also eine einparametrige Schar von Lšsungen.
3.2 Vom Sehnenviereck zum Tangentenviereck
Wir zeichnen zum Tangentenviereck die vier Ankreise gemŠ§ Abbildung 5.
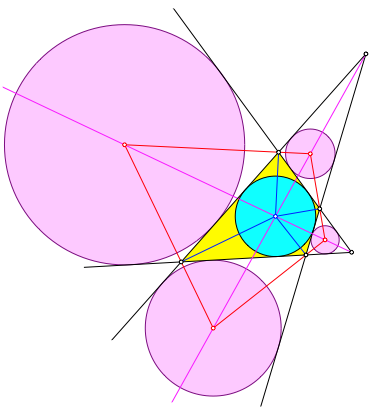
Abb. 5: Ankreise an das Tangentenviereck
Die Zentren dieser Ankreise sind die vier Ecken des Sehnenviereckes gemŠ§ der Konstruktion der Abbildung 1. Die Diagonalen dieses Sehnenviereckes sind nun aber Winkelhalbierende gegenźberliegender Seiten des Tangentenvierecks. Insbesondere ist ihr Schnittpunkt das Zentrum des Inkreises des Tangentenviereckes. Der Schnittpunkt der Diagonalen des Sehnenviereckes ist der Mittelpunkt des Inkreises des Tangentenviereckes. Daraus folgt die Stimmigkeit der Konstruktion der Abbildung 2.
Wie wir in der Abbildung 4 gesehen haben, ergeben sich weitere Lšsungen durch Verdrehen. Bei diesem Verdrehen bewegen sich die Eckpunkte des Sehnenviereckes auf Ortsbogen, welche durch den Inkreismittelpunkt und die Eckpunkte des Tangentenviereckes gegeben sind (Abb. 6). Dabei verdrehen sich die Diagonalen des Sehnenviereckes um denselben Winkel und gehen immer noch durch den Inkreismittelpunkt des Tangentenviereckes.
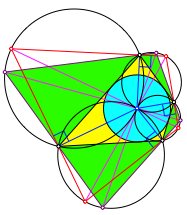
Abb. 6: Verdrehen mit Ortsbogen
Damit ergibt sich eine Erweiterung der in der Abbildung 2 angegebenen Konstruktion des Tangentenviereckes auf der Basis des Sehnenviereckes: ZunŠchst zeichnen wir wieder den Diagonalenschnittpunkt des Sehnenviereckes. Statt der Lote fŠllen wir nun ăschrŠge LoteŇ, also Linien, welche gegenźber den Loten alle um den gleichen Winkel im gleichen Drehsinn verdreht sind. Die Fu§punkt dieser Linien definieren ein Tangentenviereck (Abb. 7). Wir haben also auch hier eine einparametrige Schar von Lšsungen.
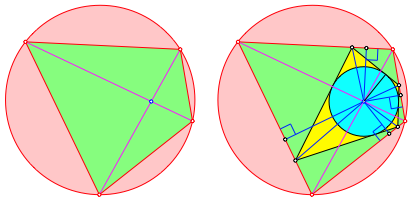
Abb. 7: Weitere Lšsung