Hans Walser, [20191217]
Sehnendreiecke
1 Worum geht es?
Spiel im Raum mit gleichseitigen Dreiecken im Umfeld des Satzes von Pythagoras.
2 Pythagoras mit gleichseitigen Dreiecken
Wir kšnnen in der Pythagoras-Figur die Quadrate durch gleichseitige Dreiecke ersetzen (Abb. 1a). Das Hypotenusendreieck kšnnen wir in zwei HŠlften unterteilen (Abb. 1b).
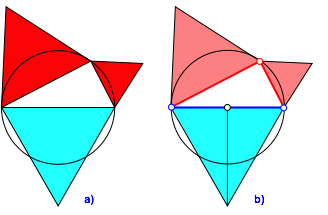
Abb. 1: Rot = blau
3 Im Raum
Die Abbildung 2 zeigt die Situation ăverrŠumlichtŇ. Der Thaleskreis ist horizontal gedacht, die beiden roten Dreiecke senkrecht nach oben geklappt und die beiden blauen Dreiecke nach unten. Es ist immer noch der FlŠchensatz rot = blau.
Die Hypotenuse zerlegen wir in zwei Radiusstrecken, die einen Winkel von 180ˇ einschlie§en.
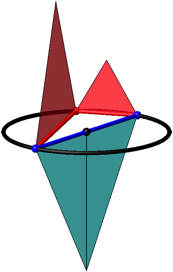
Abb. 2: Im Raum
In der Animation 1 wird der rote Punkt auf dem Thaleskreis bewegt.
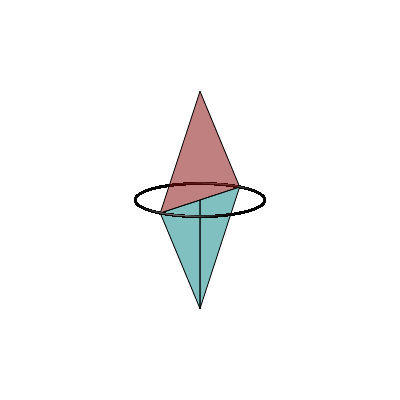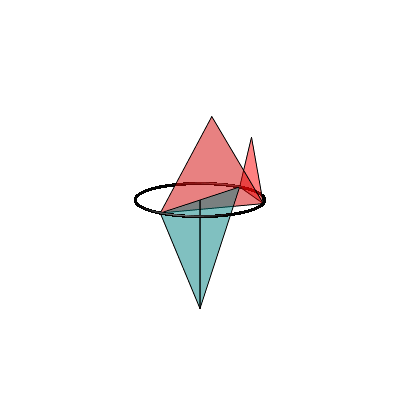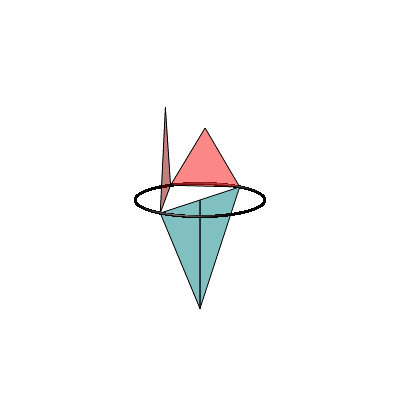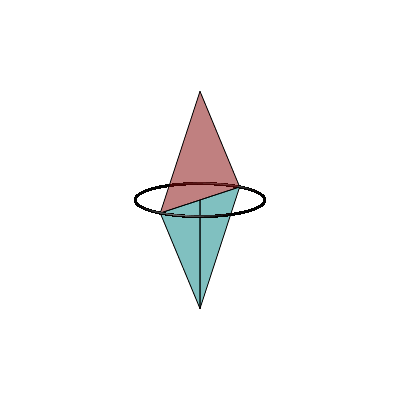
Animation 1
4 Der 3-Stern
Wir ersetzen die Hypotenuse durch einen Stern aus drei Radien, welche untereinander gleiche Winkel von 120ˇ einschlie§en (Abb. 3).
![]()
Abb. 3: 3-Stern
Weiter wŠhlen wir auf dem Thaleskreis einen Punkt, den wir mit den Enden des 3-Sternes verbinden (Abb. 4). Die drei entstehenden Sehnen schlie§en untereinander Winkel von 60ˇ und Vielfachen davon ein. Dies folgt aus KreiswinkelsŠtzen.
![]()
Abb. 4: Sehnen
Diese drei roten Sehnen źbernehmen nun die Rolle der beiden Katheten.
Nun errichten wir auf den roten Sehnen gleichseitige Dreiecke nach oben. An die blauen Radien hŠngen wir halbe gleichseitige Dreiecke an (Abb. 5).
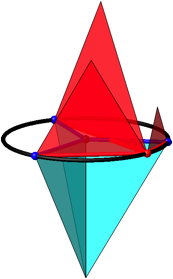
Abb. 5: Rot = blau
Auch in dieser Situation gilt der FlŠchensatz rot = blau. Der Beweis folgt aus der entsprechenden Aussage źber Sehnenquadrate.
In der Animation 2 wird der rote Punkt auf dem Thaleskreis bewegt.
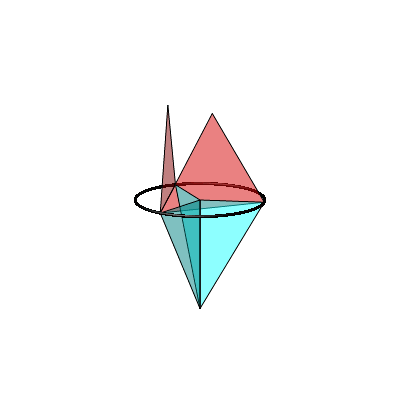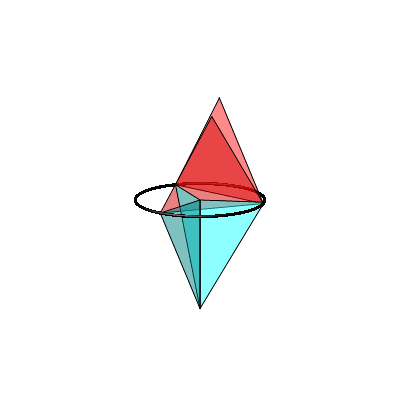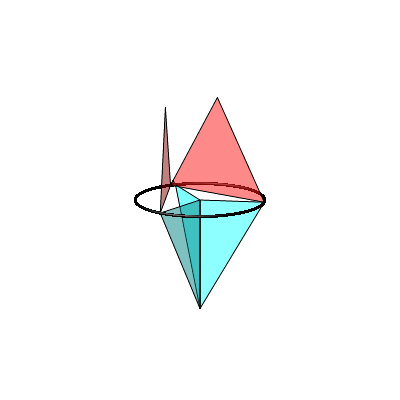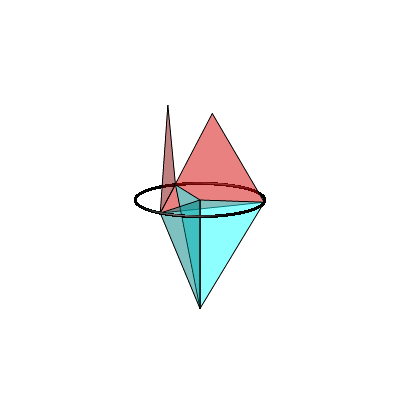
Animation 2
5 Der n-Stern
5.1 Der Fźnfstern
Die Abbildungen 6 und 7 zeigen einen 5-Stern mit zugehšrigen Sehnen sowie den Dreiecken. Wo ist das kleinste rote Dreieck?
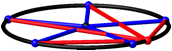
Abb. 6: 5-Stern
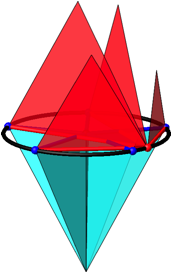
Abb. 7: Dreiecke
Wiederum gilt rot = blau.
In der Animation 3 wird der rote Punkt auf dem Thaleskreis bewegt.

Animation 3
5.2 Der 48-Stern
Die Abbildung 8 zeigt einen 48-Stern mit den Dreiecken.
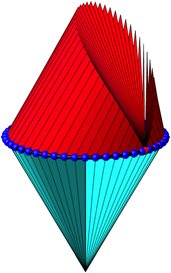
Abb. 8: 48-Stern
In der Animation 4 wird der rote Punkt auf dem Thaleskreis bewegt.

Animation 4
6 Gratkurve
Zum Studium der in der Abbildung 8 erkennbaren Gratkurve arbeiten wir mit n = 48 und einem speziell gewŠhlten roten Punkt. ZusŠtzlich sind die Spitzen der gleichseitigen Dreiecke mit einem gelben Punkt markiert (Abb. 9).
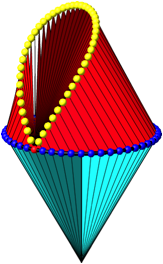
Abb. 9: Gratkurve
Die Abbildung 10 zeigt Grund-, Auf- und Kreuzriss der Figur. Ich vermute, dass es sich bei der Gratkurve um eine (affin verzerrte) vivianische Kurve handelt.
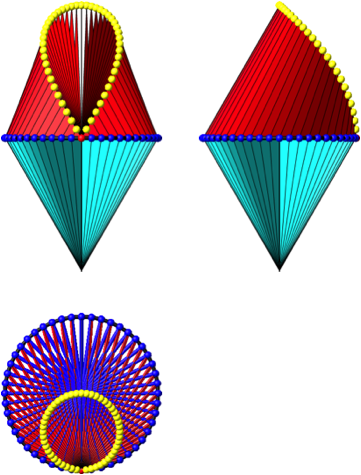
Abb. 10: Spezielle Ansichten
7 Rechtwinklig gleichschenklige Dreiecke
Das ganze Spielchen kann auch mit rechtwinklig gleichschenkligen Dreiecken durchgefźhrt werden.
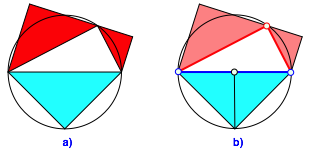
Abb. 11: Rot = blau
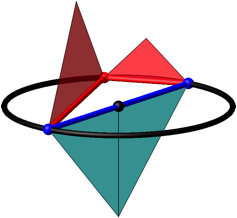
Abb. 12: VerrŠumlichung
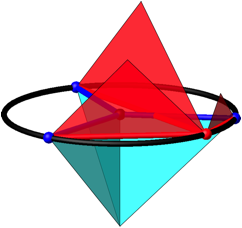
Abb. 13: Dreistern
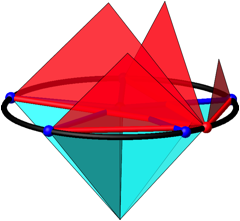
Abb. 14: Fźnfstern
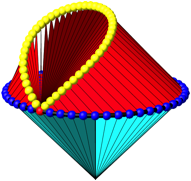
Abb. 15: Gratkurve
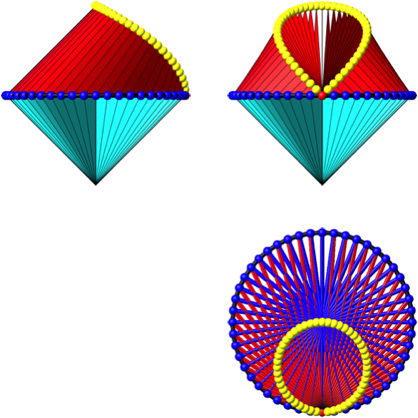
Abb. 16: Risse
Die Gratkurve ist eine vivianische Kurve. Das Innere der Gratkurve ist eine KegelflŠche.
Websites
Hans Walser: Sehnenquadrate
http://www.walser-h-m.ch/hans/Miniaturen/S/Sehnenquadrate/Sehnenquadrate.htm
Hans Walser: Umkreis bei regelmŠ§igen Vielecken
http://www.walser-h-m.ch/hans/Miniaturen/U/Umkreis/index.html