Hans Walser, [20191111], [20200102]

Sehnenquadrate

1 Worum geht es?

Verallgemeinerung des Thaleskreises und des Satzes von Pythagoras

2 Klassische Darstellung

Die Abbildung 1a zeigt die klassische Figur.

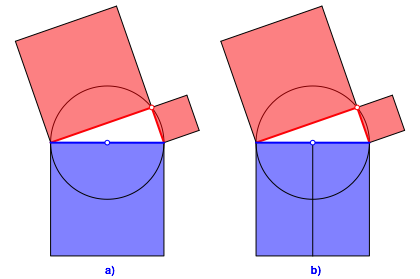
Abb. 1: Rot = blau

In der Abbildung 1b ist das Hypotenusenquadrat in zwei stehende Rechtecke mit dem Seitenverhältnis 2:1 unterteilt. Das ist zunächst eine Referenz an den Mittelpunkt des Thaleskreises.

Und nun machen wir folgendes. Wir halten den Thaleskreis horizontal und biegen die beiden Kathetenquadrate senkrecht nach oben (Abb. 2a). Die beiden Hypotenusenrechtecke lassen wir senkrecht nach unten fallen.

Die Abbildung 2b zeigt ein Kartonmodell dazu.

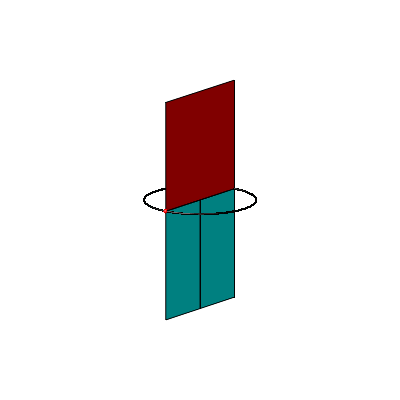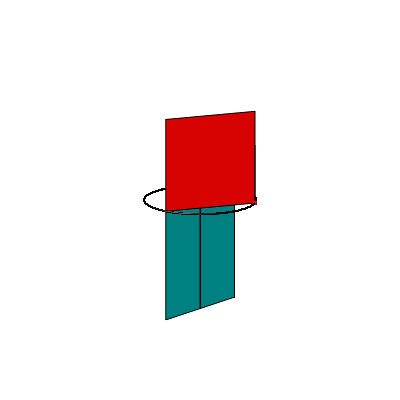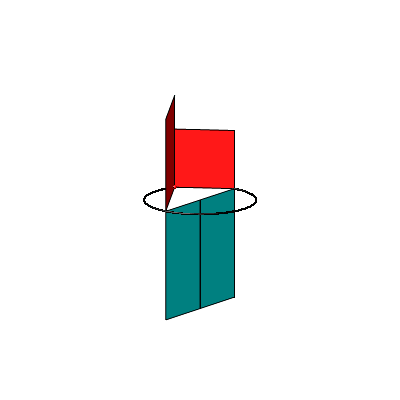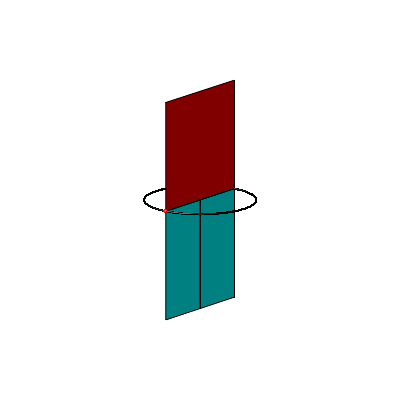
Die Abbildung 3 zeigt eine aus der Figur der Abbildung 2 abgeleitete etwas unübliche Abwicklung der Figur in die Ebene. Die beiden Hypotenusenrechtecke sind propellerartig angeordnet.

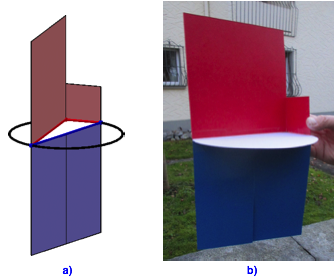
Abb. 2: Positionieren im Raum. Kartonmodell

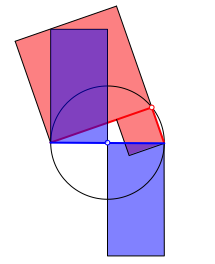
Abb. 3: Abwicklung in die Ebene

3 Variationen

3.1 Drei Kathetenquadrate

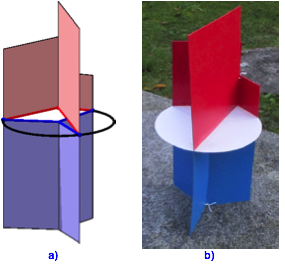
Abb. 4: Rot = blau

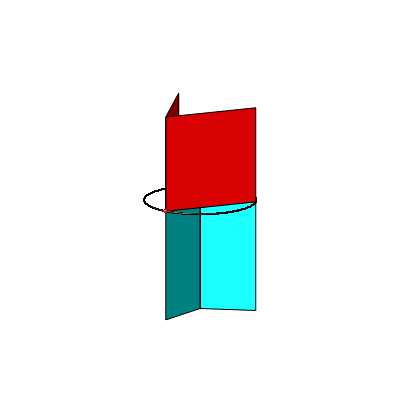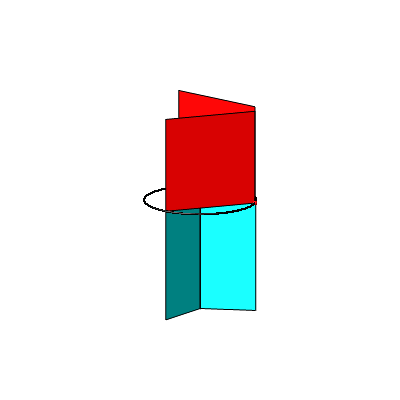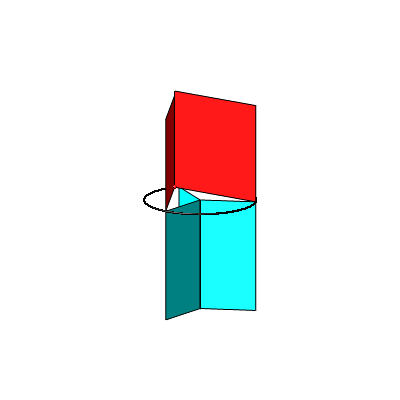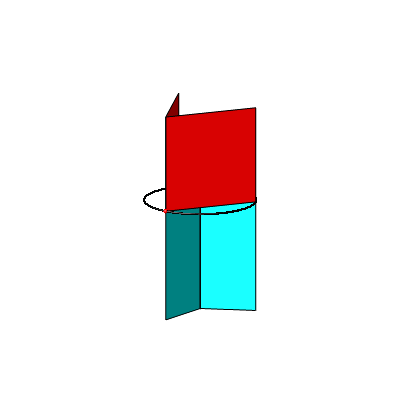
In der Abbildung 4a haben wir nun drei Kathetenquadrate und drei Hypotenusenrechtecke. Die Abbildung 4b zeigt ein Kartonmodell dazu.

Die Abbildung 5a zeigt die Situation von oben.

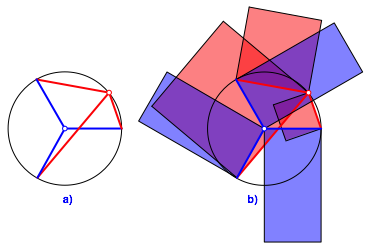
Abb. 5: Sicht von oben. Abwicklung in Ebene

Es ist folgendes gemacht worden. Die Hypotenuse wurde ersetzt durch einen 3-Stern (Mercedes-Stern). Auf dem Umkreis, den wir immer noch Thaleskreis nennen, wurde ein beliebiger Punkt gewählt. Dieser wurde mit den drei Enden des 3-Sternes verbunden. Die drei Verbindungssehnen schneiden sich unter 60°.

Über den Sehnen errichten wir Quadrate, unter den Radien des 3-Sterns hängen wir Rechtecke mit dem Seitenverhältnis 2:1 an.

Wir haben nach wie vor die Flächenbeziehung rot = blau. Die Summe der Kathetenquadrate entspricht der Summe der Hypotenusenrechtecke.

Die Abbildung 5b zeigt eine Abwicklung der Figur der Abbildung 4 in die Ebene. Die drei Hypotenusenrechtecke sind propellerartig angeordnet.

3.2 Vier Kathetenquadrate

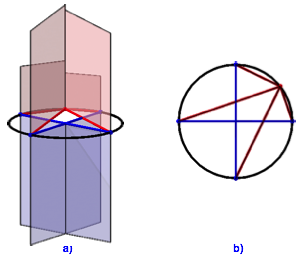
Abb. 6: Rot = blau

Die Beziehung rot = blau ergibt sich bei vier Kathetenquadraten (Abb. 6) unmittelbar aus dem gewöhnlichen Satz des Pythagoras, der hier zweimal angewendet werden kann.

3.3 Fünf Kathetenquadrate

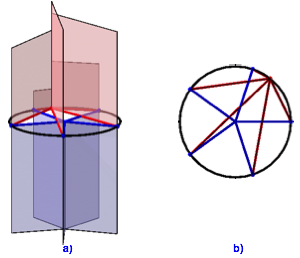
Abb. 7: Rot = blau

3.4 Allgemein

Für die folgenden Überlegungen nehmen wir den Einheitskreis als Thaleskreis.

Den Mittelpunkt des Thaleskreises verbinden wir mit n Radien mit n gleichmäßig auf dem Kreis verteilten Punkten (n-Stern). Unter diese Radien hängen wir je ein Rechteck (blau) mit der Länge des Radius und der doppelten Höhe. Sie haben also je den Flächeninhalt 2. Die Gesamtfläche der Rechtecke ist also 2n.

Von einem beliebigen Punkt P des Thaleskreises aus zeichnen wir nun die Sehnen zu den n gleichmäßig verteilten Punkten. Über jeder Sehne errichten wir ein Quadrat (rot).

Dann gilt:

Die Summe aller Flächen der roten Quadrate ist gleich der Summe der Flächen aller blauen Rechtecke, also 2n.

4 Beweis

Wir führen den Beweis rechnerisch unter Verwendung folgender Schreibweisen.

Die n gleichmäßig verteilten Punkte sind:

(1)

Der frei auf dem Thaleskreis gewählte Punkt P ist:

(2)

4.1 Hin

Wir haben zu zeigen, dass die Summe der Quadratflächen über den Sehnen, also die Summe der Quadrate der Sehnenlängen, 2n beträgt.

Für das Quadrat einer Sehnenlänge gilt:

(3)

Die Summe der Quadratflächen ist also:

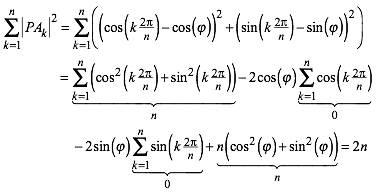(4)

Somit ist die Summe der Quadratflächen gleich der Summe der Rechteckflächen.

4.2 Zurück

Wir haben zu zeigen: ein Punkt P in der Ebene, für den die Summe der Quadrate der Verbindungsstrecken zu den n regelmäßig auf dem Einheitskreis verteilten Punkten 2n ist, liegt auf dem Einheitskreis.

Wir bezeichnen den Punkt P mit . Damit erhalten wir für unsere Bedingung:

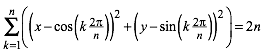(5)

Umgeformt:

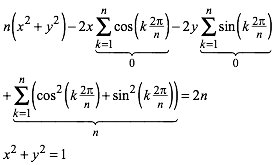(6)

Dies war zu beweisen.

Der Punkt P liegt also genau dann auf dem Kreis, wenn rot = blau ist.

Es gibt allerdings auch Lösungen im Raum, die nicht auf dem Einheitskreis liegen.

Beispiel: Es sei n = 3. Der Einheitskreis mit den drei regelmäßig verteilten Punkten liege in der x,y-Ebene. Der Punkt hat von den drei Punkten je den Abstand .

Die Summe der Quadrate der Abstände ist also 6, womit die Bedingung (5) erfüllt ist. Sämtliche Punkte auf der Einheitskugel erfüllen die Bedingung (5).

Weblinks

Hans Walser: Kreis

http://www.walser-h-m.ch/hans/Miniaturen/K/Kreis2/Kreis2.htm

Hans Walser: Al-Sijzī

http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi/Al-Sijzi.htm

Hans Walser: Al-Sijzi

http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi3/Al-Sijzi3.htm