Hans Walser, [20240627]

Sehnentangentenviereck

1 Problemstellung

Von einem Sehnentangentenviereck ABCD sind der Umkreismittelpunkt U, der Inkreismittelpunkt I und die Ecke A bekannt (Abb. 1).

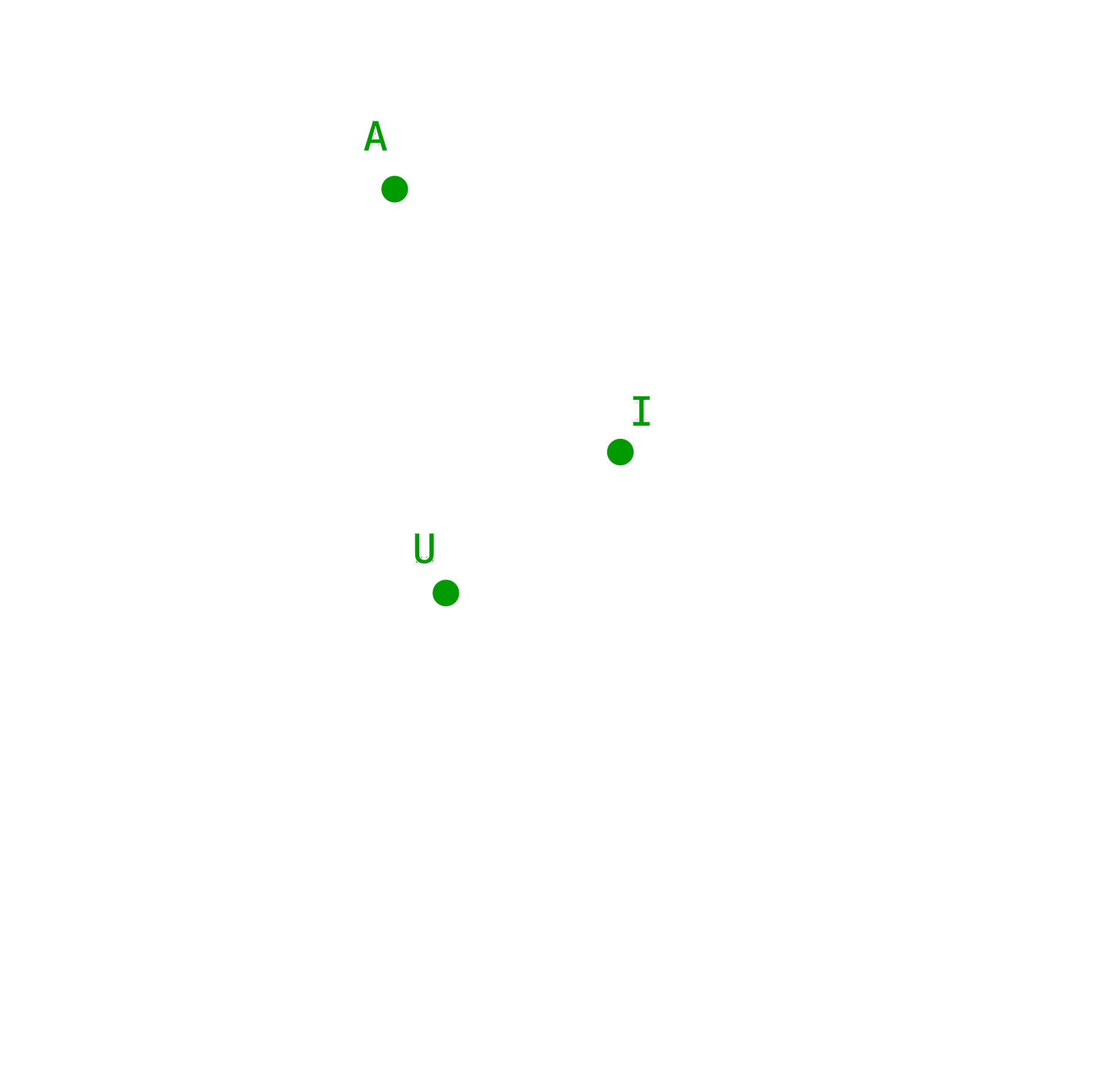
Abb. 1: Gegebene Daten

Die Abbildung 2 zeigt das passende Sehnentangentenviereck.

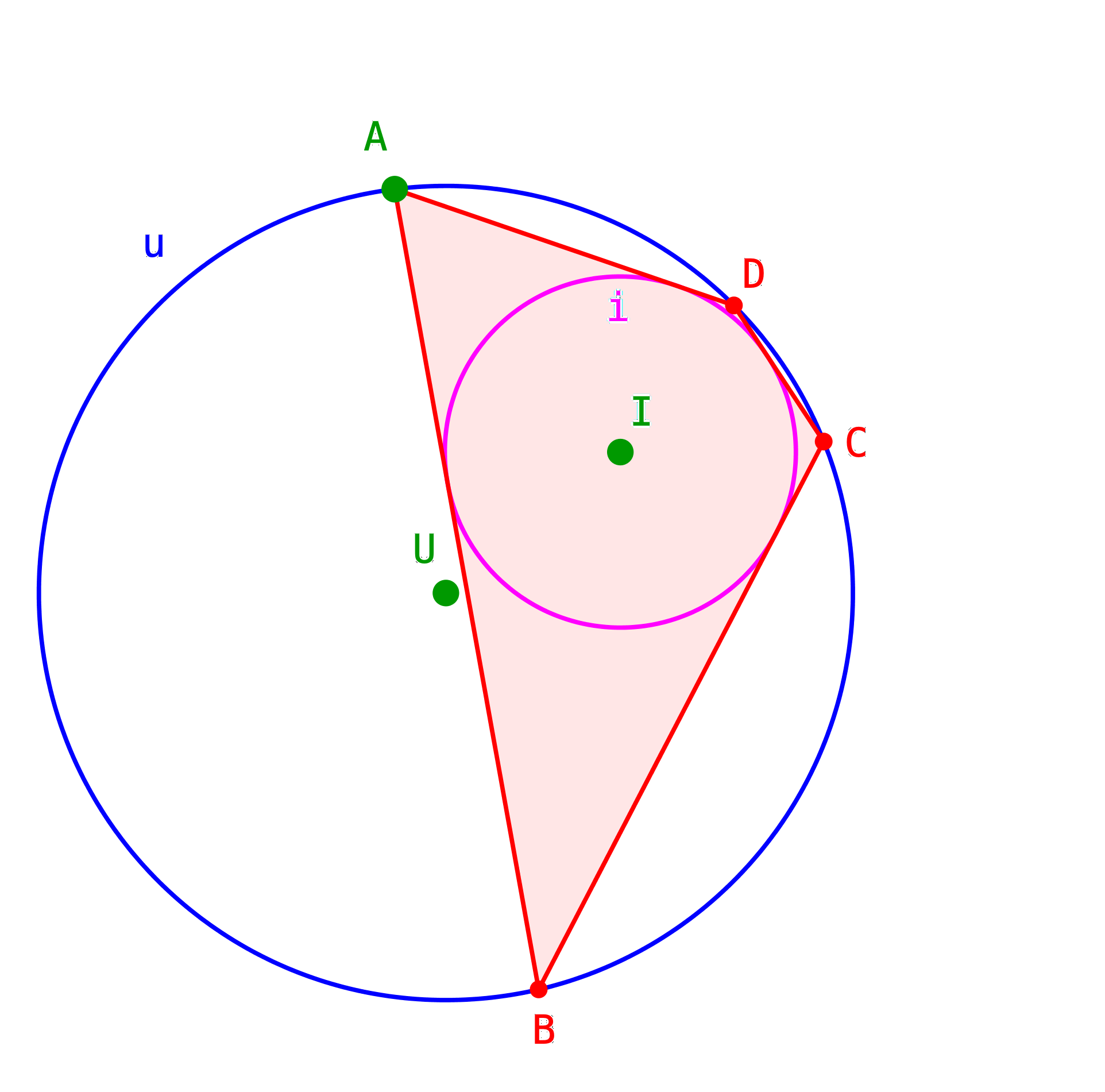
Abb. 2: Sehnentangentenviereck

Die Aufgabe ist klar: wie finden wir dieses Sehnentangentenviereck?

2 Bearbeitung

2.1 Umkreis

Der Umkreis u hat das Zentrum U und verläuft durch A (Abb. 3).

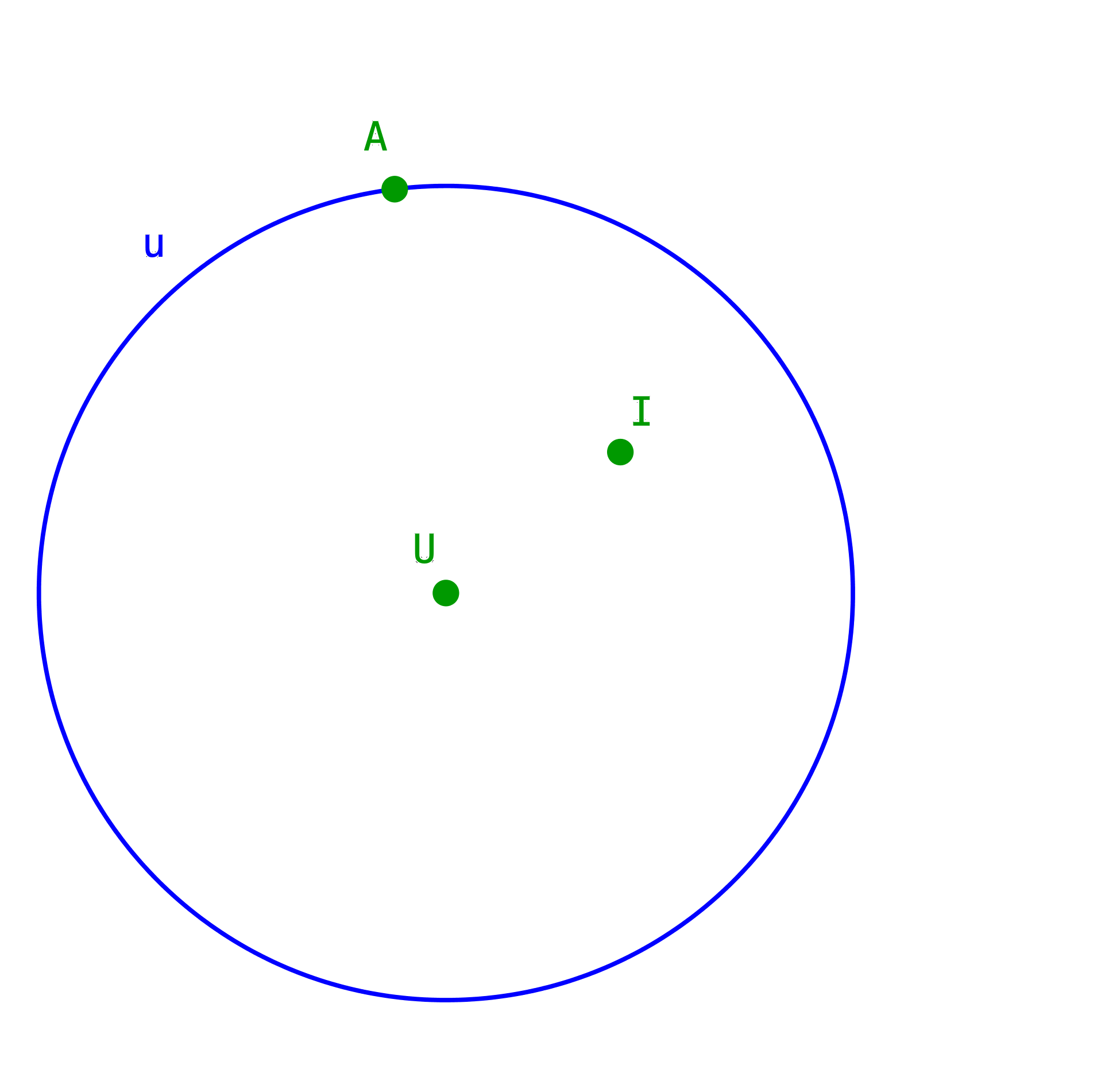
Abb. 3: Umkreis

2.2 Grundidee

Die Grundidee für die Lösung besteht nun darin, zunächst ein einfacheres Sehnentangentenviereck EFGH mit dem Umkreis u und dem Inkreismittelpunkt I zu finden. Damit kann dann der Inkreis i gezeichnet werden und nach dem Satz von Poncelet das gesuchte Sehnentangentenviereck ABCD.

Als einfacheres Sehnentangentenviereck EFGH zeichnen wir ein Drachenviereck.

2.3 Drachenviereck

Wir schneiden die Gerade e = UI mit dem Umkreis u. Schnittpunkte E und G (Abb. 4). Die Gerade e soll die Symmetrieachse des Drachenviereckes EFGH werden.

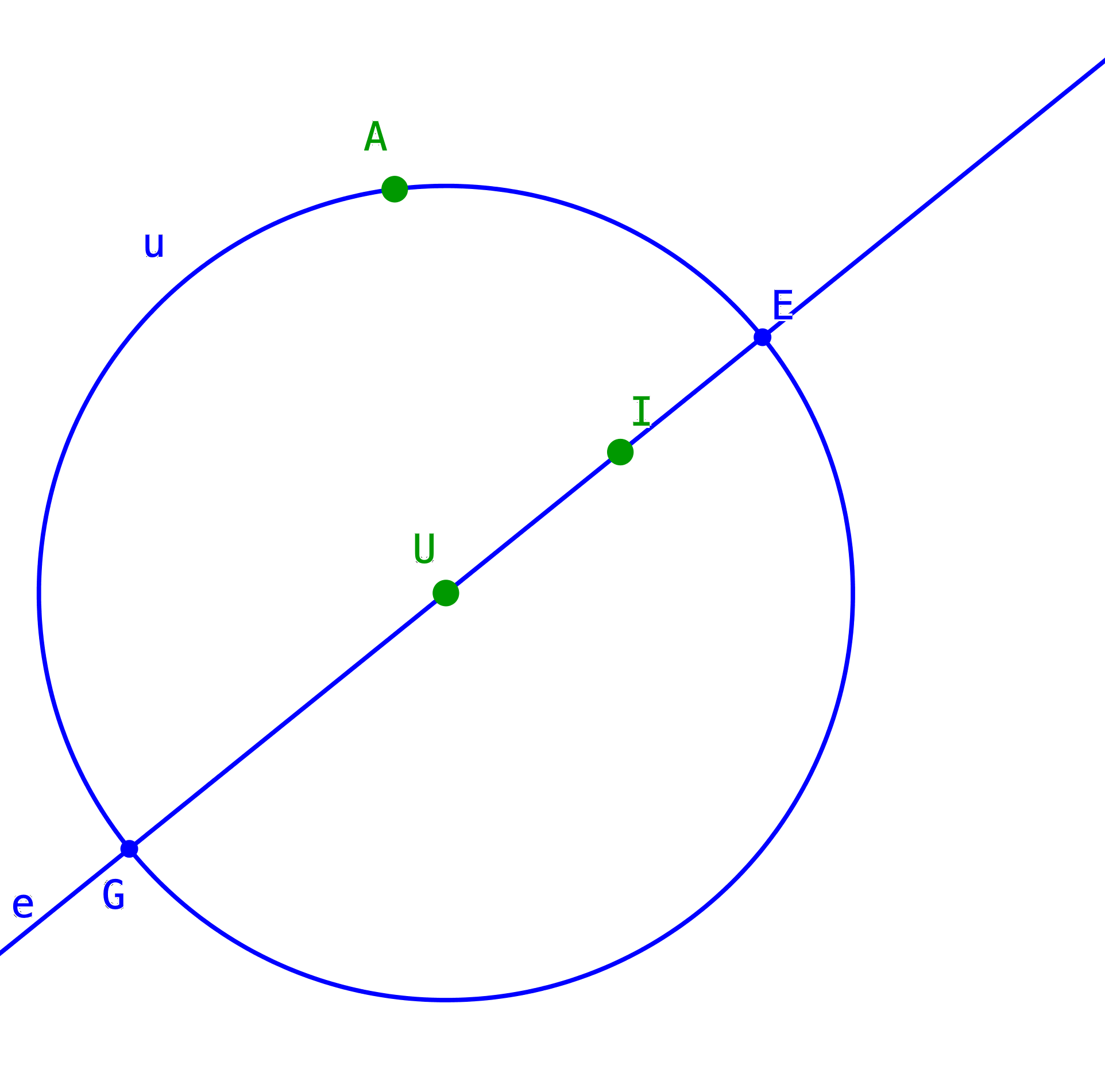
Abb. 4: Symmetrieachse

Die Punkte F und H müssen ebenfalls auf den Umkreis u zu liegen kommen.

Da im Dreieck EFG die Gerade FI eine Winkelhalbierende ist, haben wir gleiche Teilverhältnisse: |GI| : |EI| = |GF| : |EF|. Der Punkt F liegt also auf dem Apollonioskreis a zu den Punkten E und G sowie dem Verhältnis |GI| : |EI| (Abb. 5). Ebenso der Punkt H.

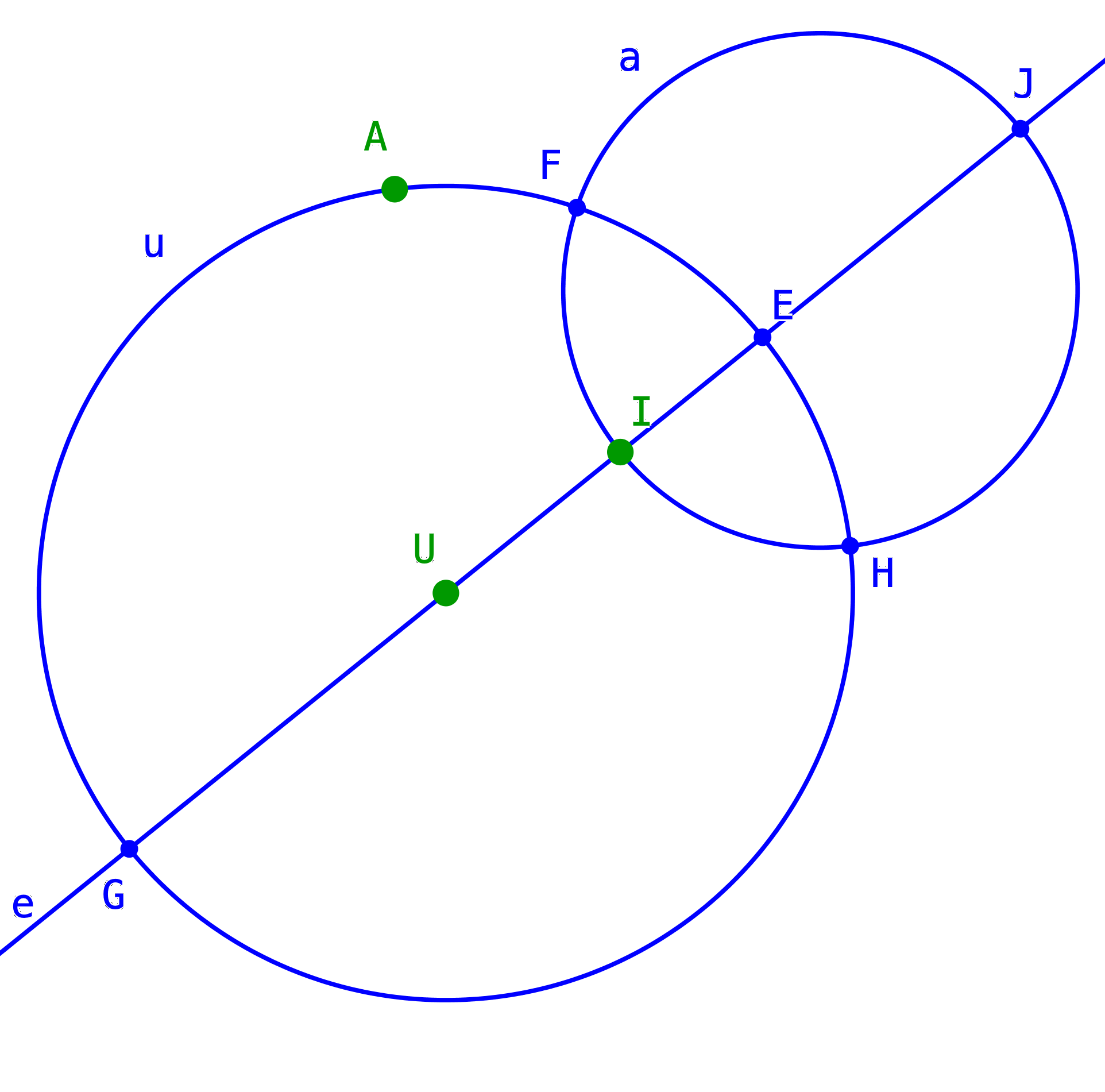
Abb. 5: Apollonioskreis

Damit können wir das Drachenviereck EFGH und seinen Inkreis i zeichnen (Abb. 6).

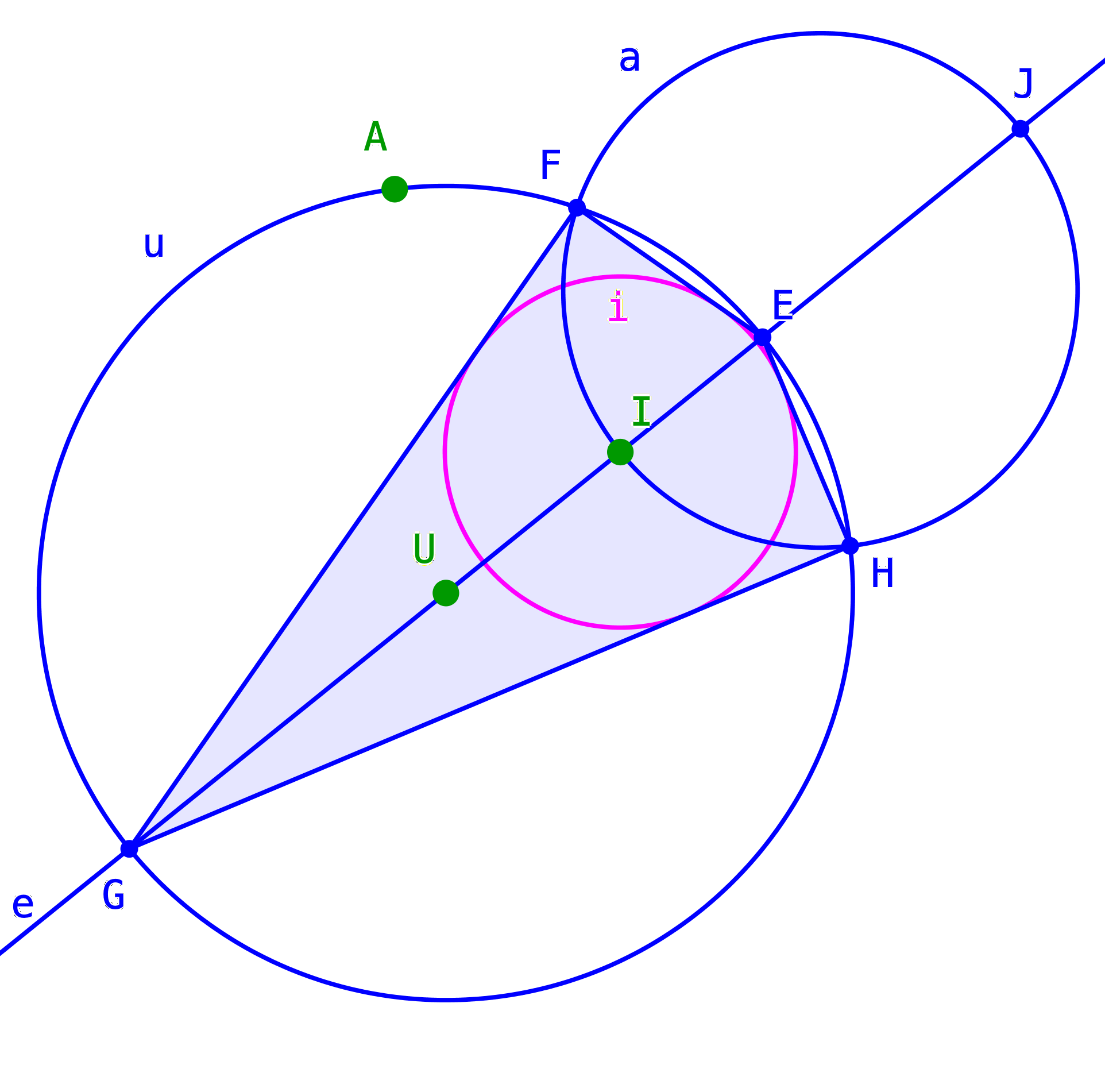
Abb. 6: Drachenviereck mit Inkreis

2.4 Poncelet

Nach dem Satz von Poncelet gibt es, wenn man einmal eine Lösung hat, unendliche viele Lösungen mit demselben Umkreis und demselben Inkreis. Dazu wählen wir einen Startpunkt, in unserem Beispiel natürlich A, auf dem Umkreis u (Abb. 7).

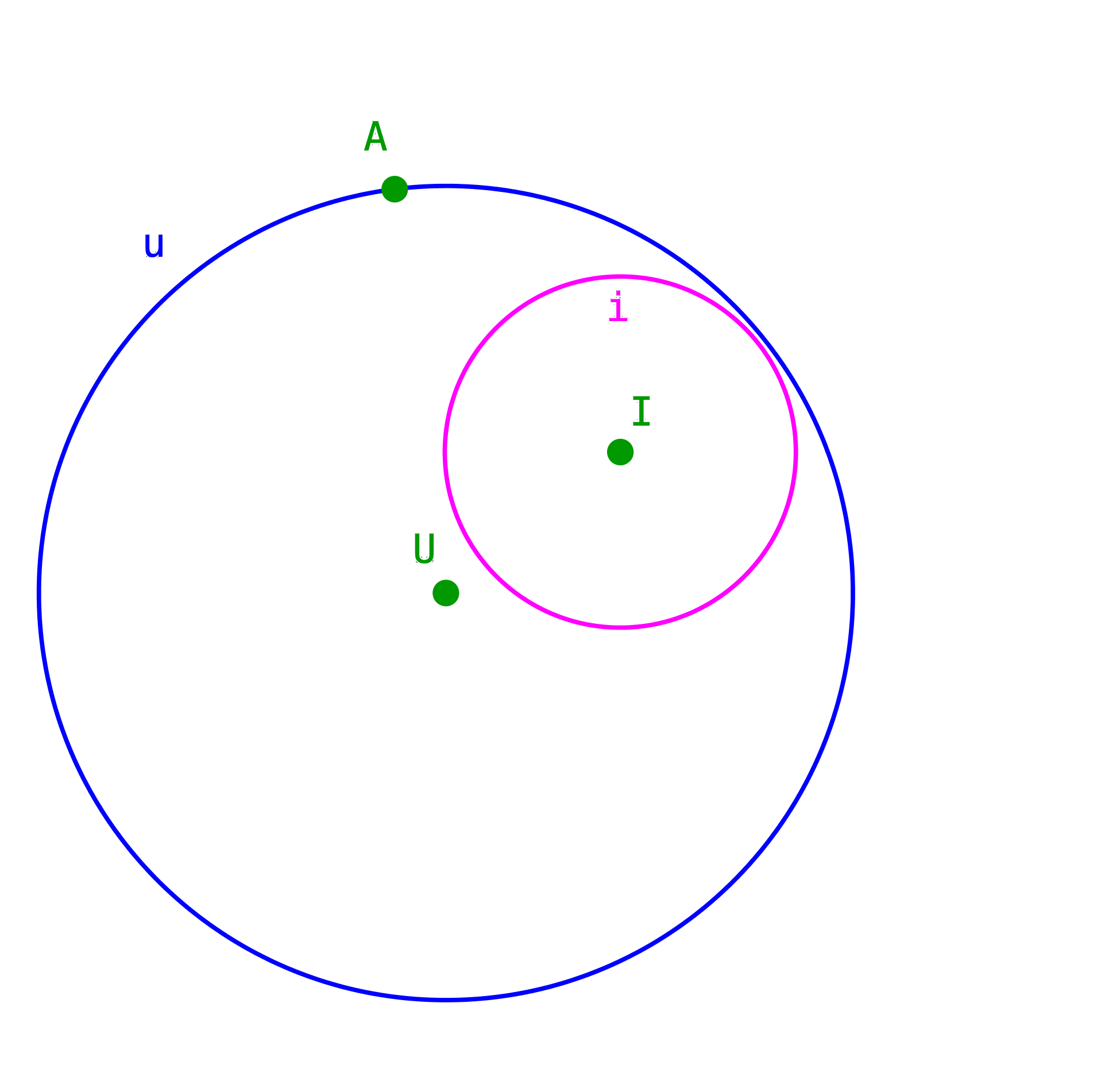
Abb. 7: Startpunkt

Mit einer Tangente an den Inkreis i kommen wir zum zweiten Punkt B auf dem Umkreis u (Abb. 8).

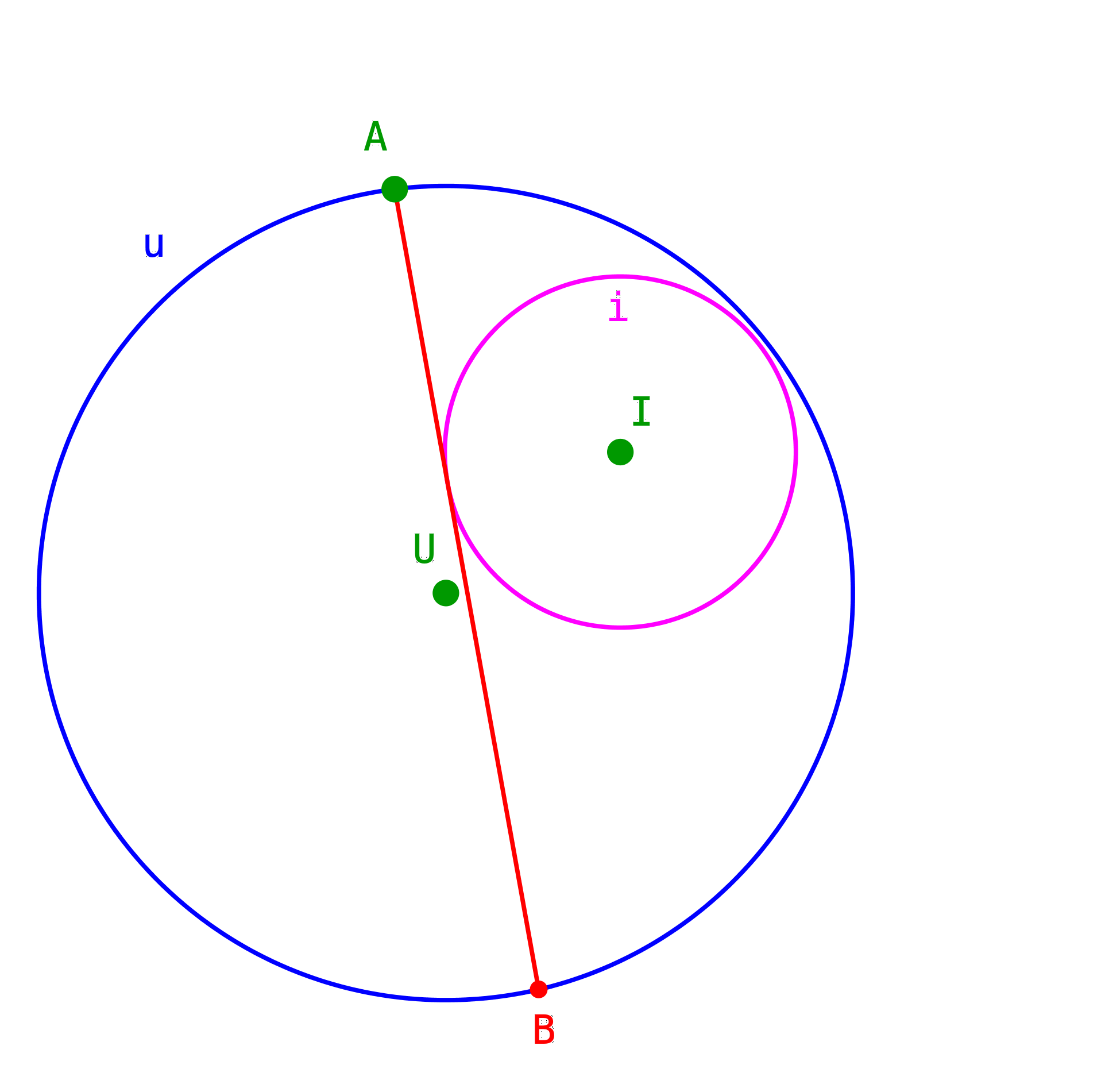
Abb. 8: Erster Schritt

Analog der zweite und dritte Schritt (Abb. 9 und Abb. 10).

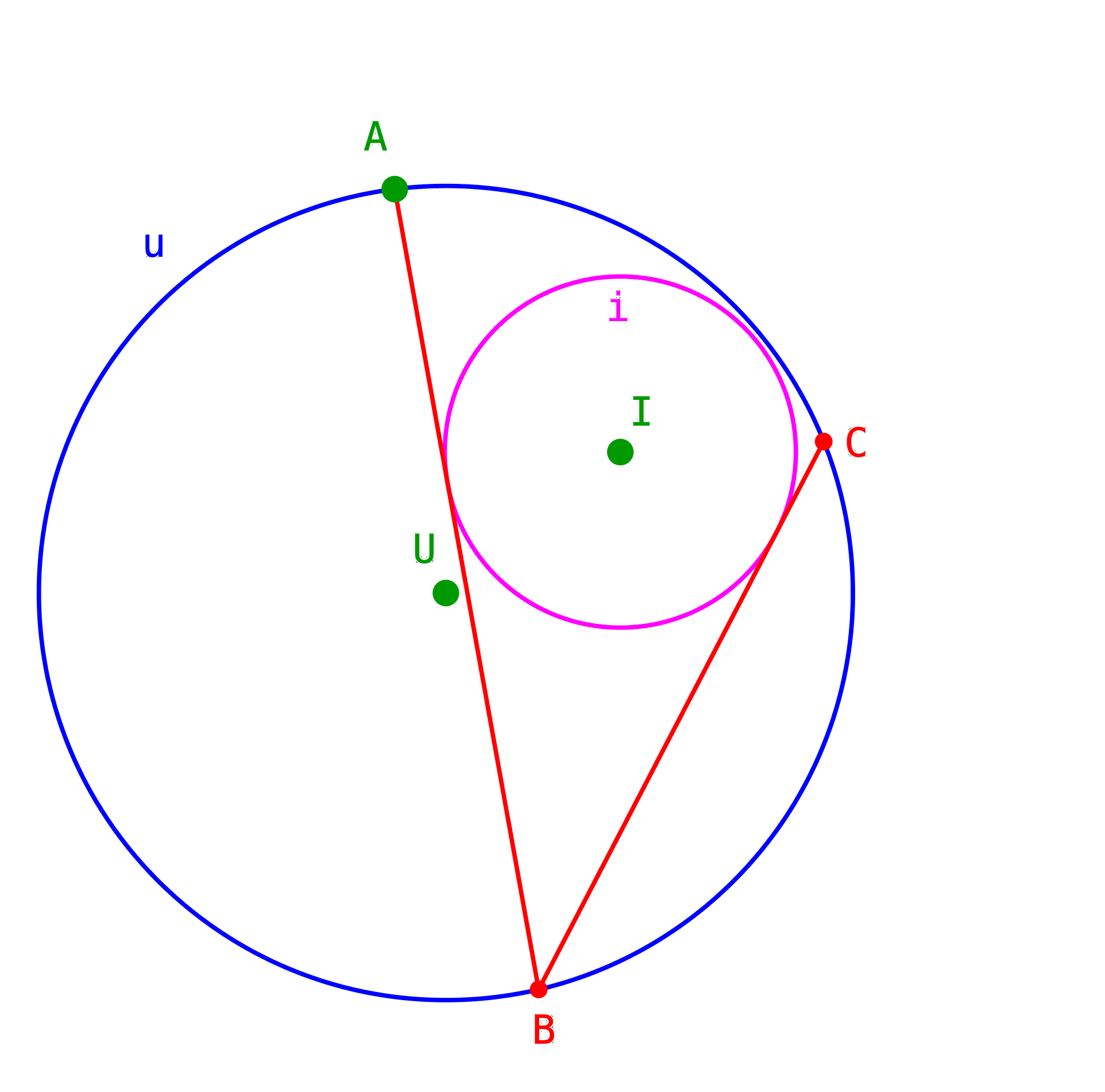
Abb. 9: Zweiter Schritt

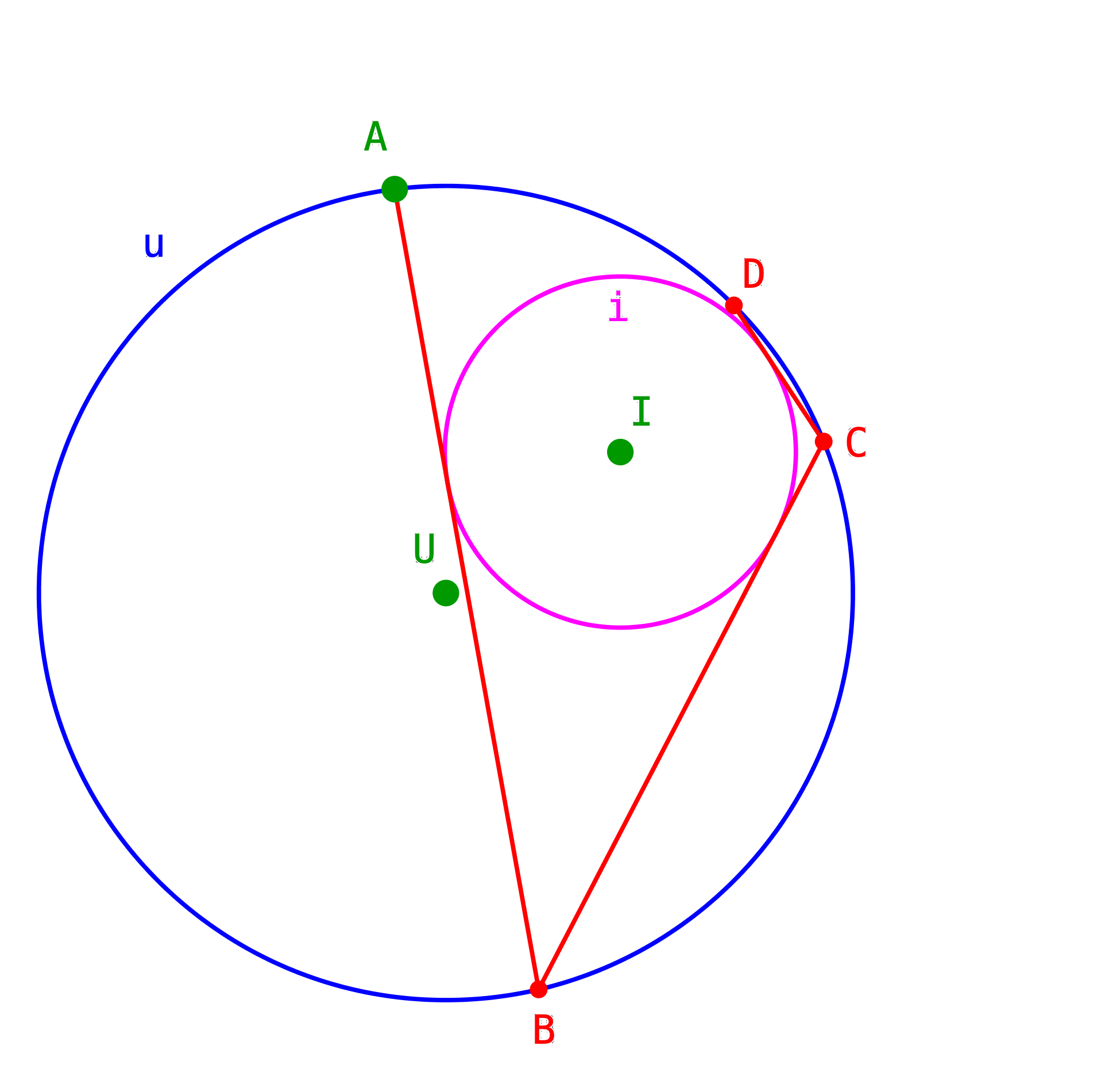
Abb. 10: Dritter Schritt

Der vierte Schritt ist bereits der letzte. Nach dem Satz von Poncelet schließt sich die Figur. Wir haben das gesuchte Sehnentangentenviereck (Abb. 11).

Abb. 11: Sehnentangentenviereck

Weblinks

Hans Walser: Sehnentangentenviereck

https://walser-h-m.ch/hans/Miniaturen/S/Sehnentangentenviereck2/Sehnentangentenviereck2.html

Hans Walser: Sehnentangentenviereck

https://walser-h-m.ch/hans/Miniaturen/S/Sehnentangentenviereck/Sehnentangentenviereck.htm