1 Das Problem

Ein Fahrzeug fährt auf einer Straße in Richtung von x an einem Verkehrsschild der Breite b vorbei, das im Abstand a von der Fahrtrichtung steht (Abb. 1). Wann ist der Sehwinkel , unter dem das Schild erscheint, am größten? (Rühenbeck 2015)

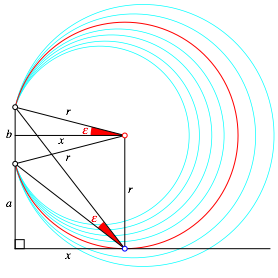
Abb. 1: Optimaler Sehwinkel

2 Klassische Lösung

Unter allen Ortsbogen über der Strecke b suchen wir den kleinsten (entspricht dem größten Winkel), der die Fahrtrichtung gerade noch erreicht, also tangential dazu ist.

Dieser Ortsbogen hat den Radius und kann daher sehr einfach konstruiert werden. Damit ist die Aufgabe konstruktiv gelöst.

Rechnerisch erhalten wir für x mit Pythagoras:

(1)

Der optimale Sehwinkel ist der halbe Zentriwinkel des Ortsbogens, also:

(2)

Das Problem lässt sich mit Mitteln der Sekundarstufe I bearbeiten.

3 Aufwärtskompatibilität

Das Problem ist ein schöner Beispiel des folgenden Extremwertproblems: Gesucht sind Extremwerte einer Funktion (in unserem Beispiel der Sehwinkel) unter der Nebenbedingung (in unserem Beispiel die Straße).

Die Nebenbedingung beschreibt einen Weg in der x,y-Ebene, und gesucht sind die Tangentialstellen zu den Niveaulinien der Funktion . Dies führt zur Bedingung, dass die beiden Gradienten linear abhängig sein müssen, also . Technisch wird dazu die Hilfsunktion gebildet, deren Gradient verschwinden muss.

Literatur

Rühenbeck, Christian (2015): Sehwinkelproblem. MNU Der mathematische und naturwissenschaftliche Unterricht 68/5 (15. 9. 2015), S. 308-309.