Hans Walser, [20190201]

Selbstunterteilung

1 Worum geht es?

Ein unregelmäßiges Dreieck soll in eine unendliche Folge von Dreiecken unterteilt werden, welche zum Ausgangsdreieck ähnlich sind.

Eine Bilderfolge.

2 Stumpfwinkliges Dreieck

Abb. 1.0: Stumpfwinkliges Ausgangsdreieck

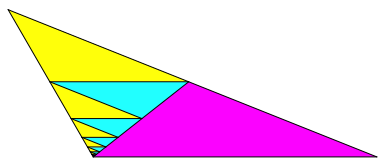
Abb. 1.1: Erste Lösung

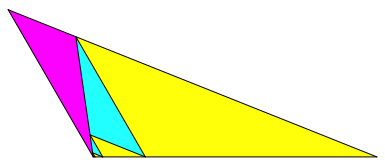
Abb. 1.2: Zweite Lösung

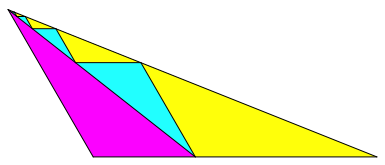
Abb. 1.3: Dritte Lösung

Die gelben Dreiecke sind jeweils gleichsinnig ähnlich zum Ausgangsdreieck, die hellblauen und das magenta Dreieck sind dazu ungleichsinnig ähnlich. Die gelben und die hellblauen Dreiecke bilden je eine geometrische Folge mit demselben Quotienten. Die hellblauen sind jeweils das geometrische Mittel der benachbarten gelben.

3 Spitzwinkliges Dreieck

Abb. 2.0: Spitzwinkliges Ausgangsdreieck

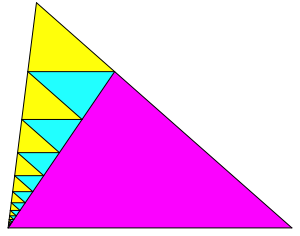
Abb. 2.1: Erste Lösung

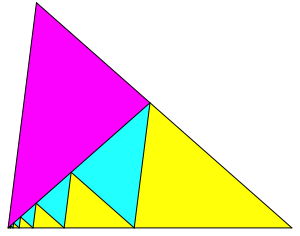
Abb. 2.2: Zweite Lösung

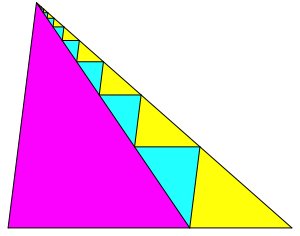
Abb. 2.3: Dritte Lösung

4 Rechtwinkliges Dreieck

Abb. 3.0: Rechtwinkliges Ausgangsdreieck

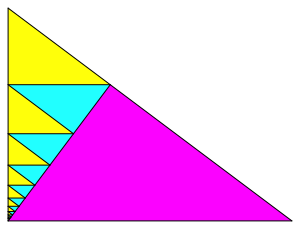
Abb. 3.1: Erste Lösung

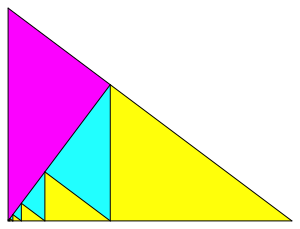
Abb. 3.2: Zweite Lösung

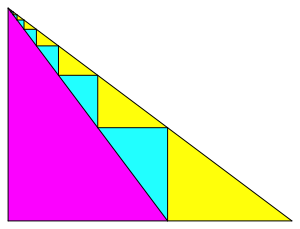
Abb. 3.3: Dritte Lösung

Bei einem rechtwinkligen Dreieck gibt es noch viele (überabzählbar viele) weitere Lösungen.

Abb. 3.4: Einfache Lösung

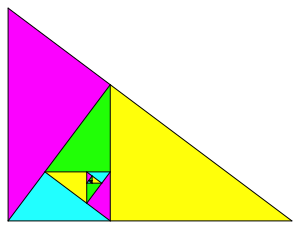
Abb. 3.5: Spiralförmige Lösung

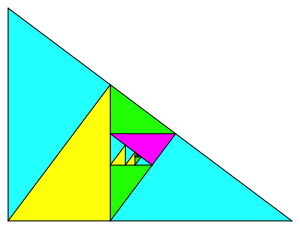
Abb. 3.6: Unregelmäßige Lösung

In [1] wird ein Beispiel mit einem gleichschenkligen Dreieck besprochen.

Websites

[1] Hans Walser: Wurzel-2-Dreieck

www.walser-h-m.ch/hans/Miniaturen/W/Wurzel-2-Dreieck/Wurzel-2-Dreieck.htm