Hans Walser, [20100730a]
Eine seltsame Gerade
1 Worum es geht
Im Umfeld der
Kiepert-Hyperbel und der Euler-Gerade finden wir eine Gerade als Ort von
Schnittpunkten.
2 Die Kiepert-Hyperbel
Einem Dreieck 
setzen wir Šhnliche gleichschenklige Dreiecke 
mit Basiswinkel 
und Spitze 
auf (Indizes
modulo 3).
Die drei Geraden 
schneiden sich
in einem Punkt S. Dies folgt aus einem
Satz von Jacobi (vgl. [Walser 2004], S. 145).
Wird der Basiswinkel 
variiert,
beschreibt S eine gleichseitige
Hyperbel, die so genannte Kiepert-Hyperbel (vgl. [Eddy/Fritsch 1994] und [Walser
2004], S. 150).
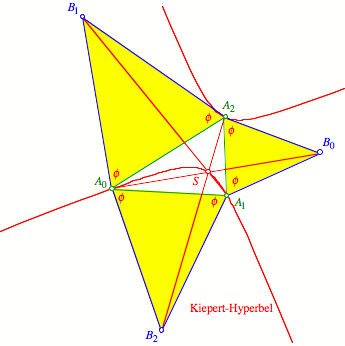
Kiepert-Hyperbel
3
Die seltsame Gerade
Nun sei 
der Schnittpunkt
der beiden Geraden 
und 
. Anschaulich gesprochen hei§t das, dass wir die Schenkel der
Dreiecke ănach untenŇ verlŠngern, bis sie sich wechselseitig schneiden.
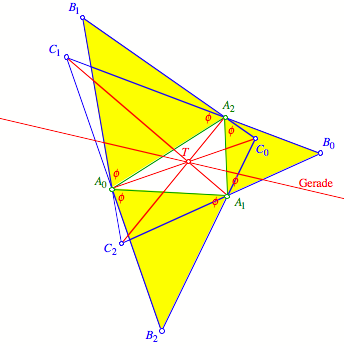
Die Gerade
Die drei Geraden 
schneiden sich
in einem Punkt T. Auch
dies folgt aus dem Satz von Jacobi.
Wird nun der Winkel 
variiert,
beschreibt T eine Gerade. Die Gerade verlŠuft
(fźr 
) durch den Umkreismittelpunkt des Dreieckes 
, ist aber nicht die Euler-Gerade.
Verifikation mit DGS.
Fragen:
á
Wie hei§t diese Gerade?
á
Beweis lege artis?
4
†berlagerung 1
Die folgende Abbildung
zeigt die †berlagerung der beiden Figuren.
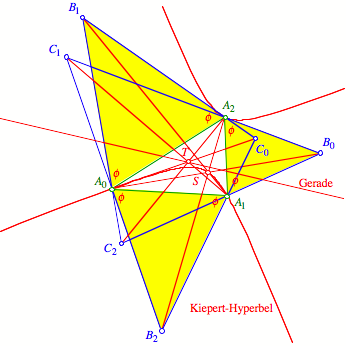
Kiepert-Hyperbel und
Gerade
Wenn wir etwa die
Gerade 
an der
Winkelhalbierenden 
des
Dreieckswinkels an der Ecke 
spiegeln, kommt
sie auf die Gerade 
zu liegen.
Verifikation DGS. Somit ist der Punkt T
eine Art ăSpiegelpunktŇ des Punktes U und unsere Gerade eine Art ăSpiegelbildŇ der Kiepert-Hyperbel.
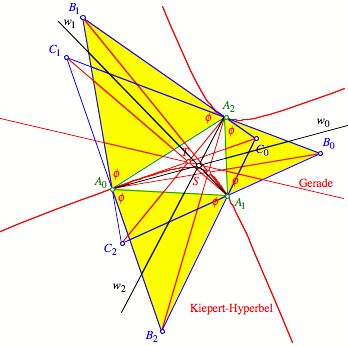
Spiegelung an
Winkelhalbierenden
5
Ein weiterer Schnittpunkt
Die drei Geraden 
schneiden sich
in einem Punkt U.
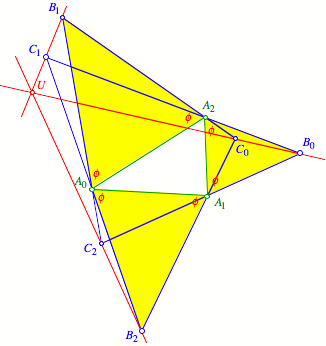
Ein weiterer
Schnittpunkt
Die drei Schnittpunkte S, T und
U sind kollinear. Verifikation
DGS.
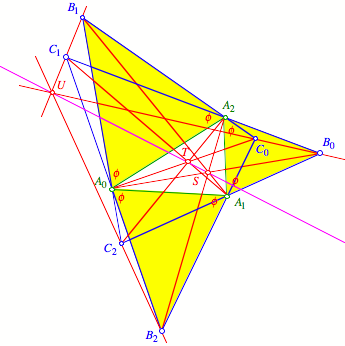
Kollineare Punkte
Bei Variation von 
beschreibt der
Punkt U eine Gerade. Diese ist nun die
Euler-Gerade. Verifikation DGS.
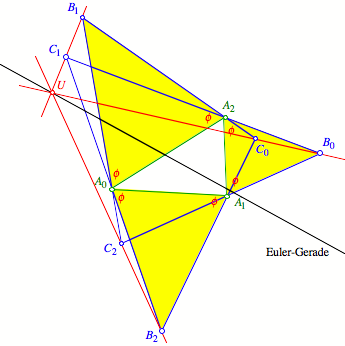
Euler-Gerade
Die Euler-Gerade kann also als Ort von Schnittpunkten erzeugt werden (vgl. [Walser 1993]).
6
†berlagerung 2
Die folgende Figur
zeigt die †berlagerung sŠmtlicher besprochener Figuren.
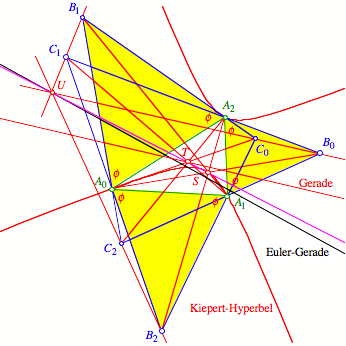
†berlagerung 2
Literatur
[Eddy/Fritsch 1994] Eddy, R.H. / Fritsch, R.: The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Mathematics Magazine. Vol. 67, No. 3, June 1994, p. 188 - 205.
[Walser 1993] Walser,
Hans: Die Eulersche Gerade als Ort "merkwźrdiger Punkte". Didaktik
der Mathematik (21), 1993, 95-98
[Walser 2004] Walser, Hans: 99 Schnittpunkte. Beispiele – Bilder – Beweise. Edition am Gutenbergplatz, Leipzig 2004. ISBN 3-937219-10-2