Hans Walser, [20210626]
Seltsamer Pythagoras
Anregung: Thomas Jahre, Aufg. 57-861
1 Problemstellung
Das rote Quadrat hat die unbekannte SeitenlŠge a. Die kurzen Katheten der rechtwinkligen Dreiecke haben der Reihe nach die LŠngen 1, 2, 3 und 4.

Abb. 1: Problemstellung
Wie gro§ muss die SeitenlŠnge a sein, damit die Hypotenuse des grš§ten rechtwinkligen Dreiecks in Linie mit der Grundseite des Quadrates liegt?
2 Bearbeitung
Die SeitenlŠnge a ist die positive Lšsung der Gleichung:

Es ist a Ĺ 5.318618244.
3 Pythagoras
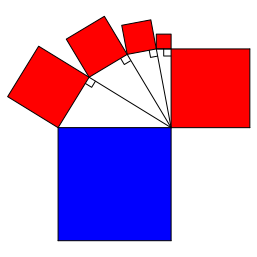
Abb. 2: Rot = blau
Die FlŠchensumme der fźnf roten Quadrate (Abb. 2) ist gleich der blauen QuadratflŠche.
Bemerkung: das Analoge gilt auch fźr andere aus rechtwinkligen Dreiecken gebauten eckigen Spiralen.
Websites
Thomas Jahre: Aufgabe der Woche
https://www.schulmodell.eu/aufgabe-der-woche.html