Hans Walser, [20170101]
Semiregulres Ikosaeder
1 Worum geht es?
Modifikation des regulren Ikosaeders unter Erhaltung der Topologie.
2 Regulres Ikosaeder
Die Abbildung 1 zeigt ein regulres Ikosaeder.
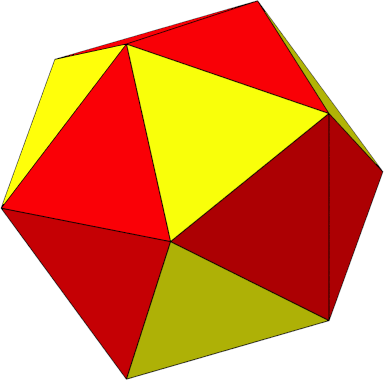
Abb. 1: Regulres Ikosaeder
Die Abbildung 2 zeigt das zugehrige Schlegel-Diagramm, welches die topologischen Verhltnisse wiedergibt.

Abb. 2: Schlegel-Diagramm
3 Semiregulres Ikosaeder
Wir
modifizieren die Figur der Abbildung 1 gem§ Abbildung 3. Zwei benachbarte rote
gleichseitige Dreiecke mit einer nach au§en gerichteten gemeinsamen Kante
ersetzen wir durch zwei benachbarte blaue Dreiecke mit einer nach innen
gerichteten gemeinsamen Kante. Die blauen Dreiecke sind nicht mehr gleichseitig.
Sie sind gleichschenklig mit einem Spitzenwinkel von 108¡. Bei der
Schenkellnge 1 haben sie die Basislnge ![]() mit:
mit:
![]() (1)
(1)
Dies ist der Goldene Schnitt (Walser 2014, S. 16).
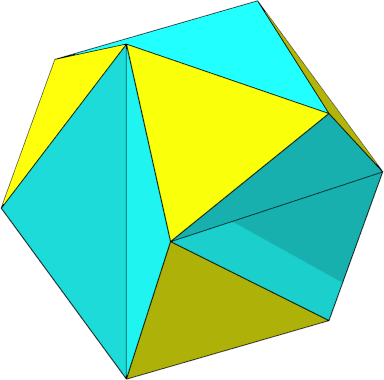
Abb. 3: Semiregulres Ikosaeder
Die Abbildung 4 zeigt eine Frontalansicht des semiregulren Ikosaeders.
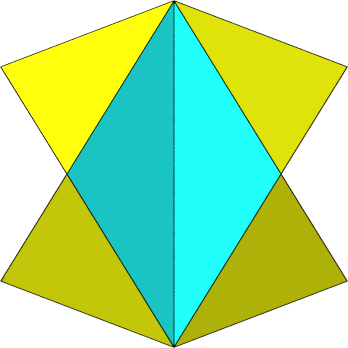
Abb. 4: Frontalansicht
Die neuen langen nach innen gerichteten Kanten sind windschief, aber orthogonal zu den weggelassenen nach au§en gerichteten Kanten zwischen den roten Dreiecken. Wir haben also gekreuzte Kanten.
Im Schlegel-Diagramm zeigt sich das gem§ Abbildung 5. Die neuen langen nach innen gerichteten Kanten sind zunchst ins alte Schlegeldiagramm (Abb. 2) blau eingezeichnet. Da das Schlegel-Diagramm nur topologische, aber keine metrische Verhltnisse wiedergibt, ist die Orthogonalitt der neuen mit den alten Kanten nicht sichtbar.
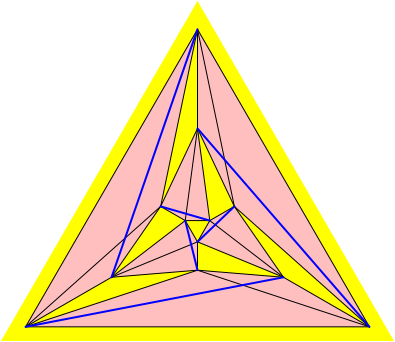
Abb. 5: Neue blaue Kanten
Die Abbildung 6 zeigt das Schlegel-Diagramm des semiregulren Ikosaeders.
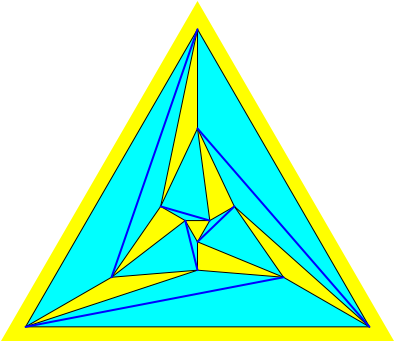
Abb. 6: Schlegel-Diagramm des semiregulren Ikosaeders
Das Kantenbild unterscheidet sich vom Kantenbild des Schlegel-Diagramms des regulren Ikosaeders (Abb. 2). Allerdings ist die Topologie dieselbe. Wir haben gleich viele Knoten, Kanten und Dreiecke. Auch treffen in jedem Knoten fnf Kanten ein.
Wir knnen die Figur unter Erhaltung der Topologie umzeichnen (Abb. 7).
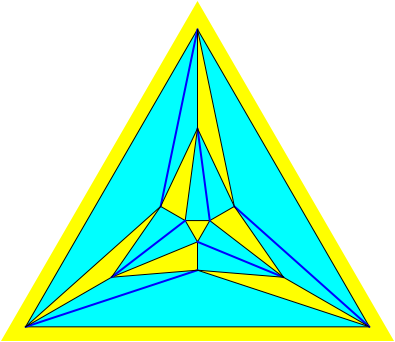
Abb. 7: Schlegel-Diagramm des semiregulren Ikosaeders
Nun sehen wir, bis auf die Farbe, keinen Unterschied mehr zum Schlegel-Diagramm des regulren Ikosaeders (Abb. 2).
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.