Hans Walser, [20210415]

Shrimps

1 Worum geht es?

Lage des Zentrums einer eckigen logarithmischen Spirale. Ortsbogen und Kreis des Apollonius. Ebene der komplexen Zahlen. Höhensatz.

2 Die Spirale

Wir starten im Ursprung und zeichnen die Strecke zum Punkt P₀ mit den Koordinaten (1,0). Mit einer Richtungsänderung t und einem Verkürzungsfaktor f < 1 hängen wir eine zweite Strecke P₀P₁ an (Abb. 1 für t = 45° und f = 0.75).

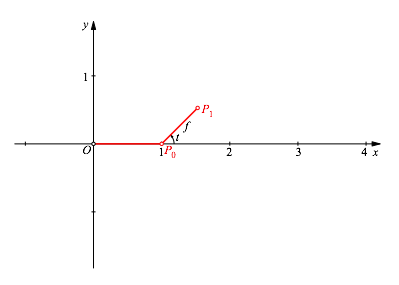
Abb. 1: Start

Durch Iteration des Prozesses entsteht eine eckige logarithmische Spirale (Abb. 2).

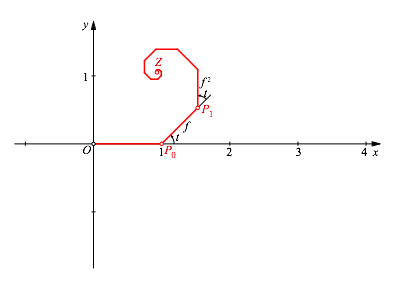
Abb. 2: Spirale

Wir fragen nach dem Zentrum Z der Spirale.

3 Das Zentrum

Das Zentrum Z finden wir wie folgt (Abb. 3): Wir zeichnen zur Strecke OP₀ einerseits den Ortsbogen für den Winkel t und andererseits den Kreis des Apollonius für das Verhältnis f. Der Schnittpunkt ist das gesuchte Zentrum Z.

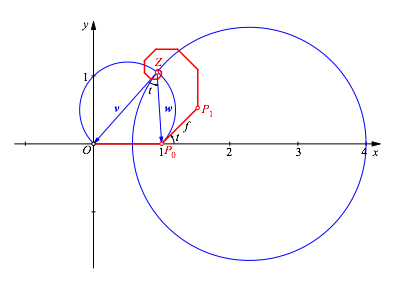
Abb. 3: Zentrum

Begründung: Die eckige logarithmische Spirale hat eine Drehstrecksymmetrie. Wenn wir sie um das Zentrum Z um den Winkel t drehen und mit dem Faktor f strecken, kommt sie mit sich selber zur Deckung. Bei dieser Drehstreckung wird der Vektor v von Z nach O auf den Vektor w von Z nach P₀ abgebildet. Daher haben diese beiden Vektoren den Zwischenwinkel t und das Längenverhältnis f. Der Zwischenwinkel t wird mit dem Ortsbogen, das Längenverhältnis f mit dem Kreis des Apollonius realisiert

4 Reihen

Wir bezeichnen die Ecken der Spirale mit O, P₀, P₁, P₂, P₃, ... . Damit hat P_n die Koordinaten:

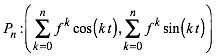(1)

Für das Zentrum Z erhalten wir durch Grenzübergang die Reihen:

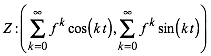(2)

Für die Reihen in (2) gilt:

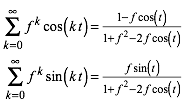(3)

Wir können die Formeln (3) verifizieren wie folgt. Wir setzen (3) in (2) ein und berechnen die Vektoren v und w. Mit einiger Rechnung stellen wir dann fest, dass diese beiden Vektoren tatsächlich den Zwischenwinkel t und das Längenverhältnis f haben.

5 In der Ebene der komplexen Zahlen

Wir können (3) aber auch mit komplexen Zahlen direkt herleiten. Dazu setzen wir:

(4)

In der Ebene der komplexen Zahlen erhalten wir die Drehstreckung mit dem Drehwinkel t und dem Streckfaktor f durch eine Multiplikation mit q. Daher ist:

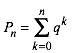(5)

Für das Zentrum Z erhalten wir die geometrische Reihe:

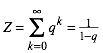(6)

Einsetzen von (4) in (6) ergibt:

(7)

Trennung in Real- und Imaginärteil liefert (3).

6 Alternative Konstruktion

Die Überlegungen in der Ebene der komplexen Zahlen führen zu einer alternativen Konstruktion des Zentrums Z.

Aus (5) ergibt sich insbesondere:

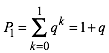(8)

Wenn wir also P₁ am Punkt P₀ spiegeln, erhalten wir Q₁ = 1 – q (Abb. 4).

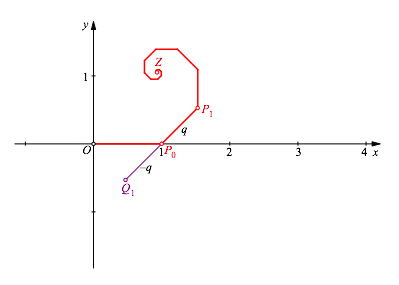
Abb. 4: Start der alternativen Konstruktion

Wegen (6) ist Z der komplexe Kehrwert von Q₁. Den komplexen Kehrwert findet man durch Spiegeldung an der reellen Achse (x-Achse) und anschließender Inversion am Einheitskreis. Es gibt dynamische Geometrie-Software mit einem direkten Button für die Kreisspiegelung. Wir zeigen ein schrittweises Vorgehen mit elementaren Mitteln (Abb. 5).

Abb. 5: Kreisspiegelung

Wir spiegeln Q₁ an der y-Achse und erhalten den Bildpunkt Q₂. (Wir hätten ebenso gut den Punkt Q₁ zunächst an der x-Achse und anschließend am Koordinatennullpunkt O spiegeln können.) Das gesuchte Zentrum Z liegt auf der Geraden Q₂O. Nun müssen wir noch die Länge der Strecke Q₂O invertieren. Dazu zeichnen wir die Normale zur Geraden Q₂O durch O und schneiden diese mit dem Einheitskreis im Punkt N. Die Normale zu Q₂N durch N scheidet die Gerade Q₂O im gesuchten Punkt Z.

Begründung: Das rechtwinklige Dreieck Q₂ZN hat die Höhe 1. Daher sind die Längen der Strecken Q₂O und OZ invers.

Diese Konstruktion der Kreisspiegelung hat gegenüber den üblichen Konstruktionen den Vorteil, dass sie unabhängig von der Lage des Ausgangspunktes innerhalb oder außerhalb des Einheitskreises funktioniert.

7 Variation der Parameter

7.1 Variation der Richtungsänderung.

Wir halten f konstant und variieren t zwischen 0° und 360° Das Zentrum Z bewegt sich auf dem Kreis des Apollonius für das Verhältnis f (Abb. 6 für f = 0.75).

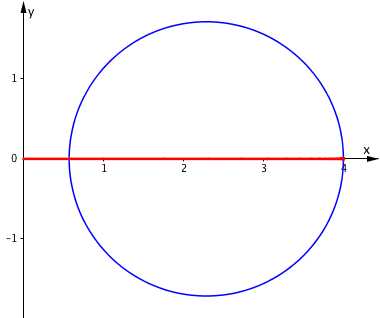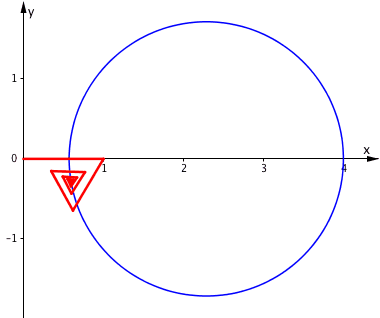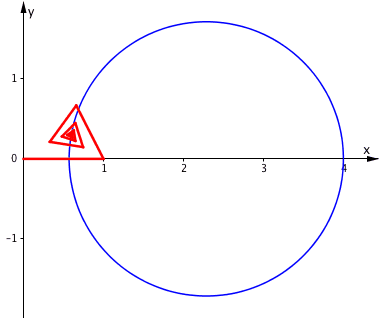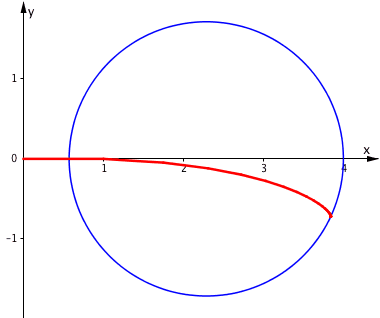
Abb. 6: Variation der Richtungsänderung

7.2 Variation des Verkürzungsfaktors

Wir halten t fest und variieren f zwischen 0 und 1. Das Zentrum Z bewegt sich auf dem Ortsbogen für den Winkel t (Abb. 7 für t = 45°).

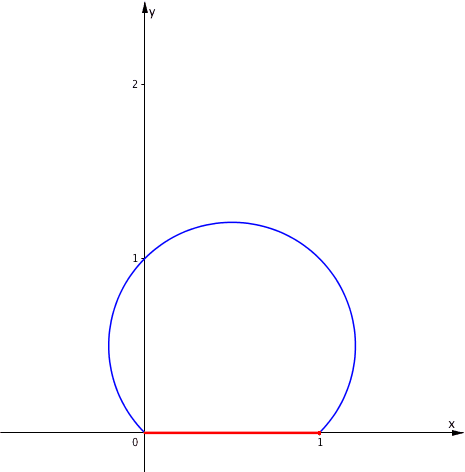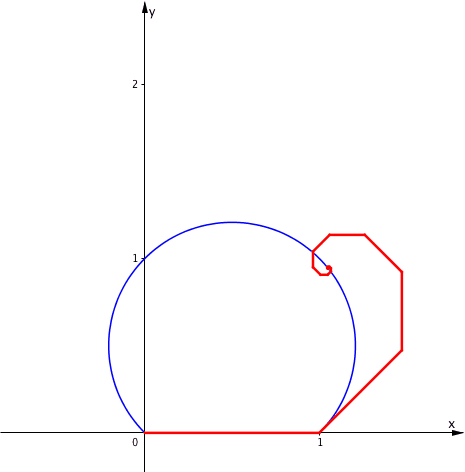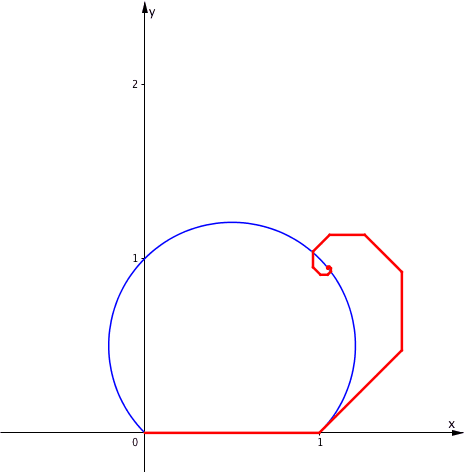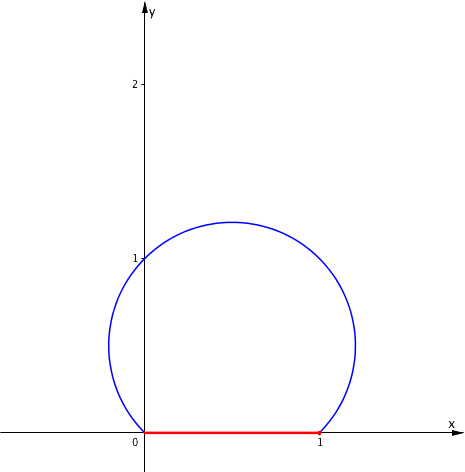
Abb. 7: Variation des Verkürzungsfaktors

Im Grenzfall f = 1 ergibt sich das regelmäßige Achteck.