Hans Walser, [20131005]

Sieb des Eratosthenes

1 Worum geht es?

Bearbeitung einer falschen Vermutung über Primzahlen.

2 Spiel mit Primzahlen

Jan addiert jeweils zwei aufeinanderfolgende Primzahlen.

Primzahl	Summe aufeinanderfolgender Primzahlen
1
	3
2
	5
3
	8
5
	12
7
	18
11
	24
13
	30
17
	36
19
	42
23

Er vermutet, dass man bei Weglassen der ersten drei Primzahlen die „Sechserreihe“ 12, 18, 24, ... erhält.

3 Gegenbeispiel

Die Vermutung ist falsch, wie das folgende Gegenbeispiel zeigt.

Primzahl	Summe aufeinanderfolgender Primzahlen
1
	3
2
	5
3
	8
5
	12
7
	18
11
	24
13
	30
17
	36
19
	42
23
	52
29

4 Einschaltzahlen

Die Vermutung kann modifiziert werden durch Einschalten weiterer Zahlen zwischen den Primzahlen.

Primzahl	Summe aufeinanderfolgender Zahlen
1
	3
2
	5
3
	8
5
	12
7
	18
11
	24
13
	30
17
	36
19
	42
23
	48
25 = 5^2
	54
29
	60
31
	66
35 = 5*7
	72
37
	78
41
	84
43
	90
47
	96
49 = 7^2
	102
53
	108
55 = 5*11
	114
59
	120
61
119
	240
121 = 11^2
	246
125 = 5^3
	252
127
	258
131

Es fällt auf, dass die roten Einschaltzahlen die Primfaktoren 2 und 3 nicht enthalten.

5 Sieb des Eratosthenes

Wir modifizieren die Idee des Eratosthenes und entfernen aus der Menge der natürlichen Zahlen die Zahlen 2 und 3 sowie die Vielfachen davon. In der Abbildung 1 sind das die zyan unterlegten Zahlen.

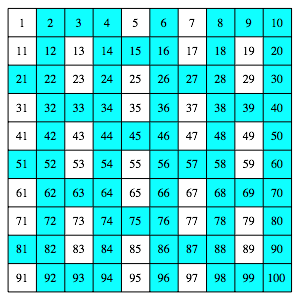
Abb. 1: Entfernte Zahlen

Dann bleiben folgende Zahlen übrig:

1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, 35, 37, 41, 43, 47, 49, 53, 55, 59, 61, 65, 67, 71, ...

Diese Zahlen sind kongruent 1 modulo 6 oder kongruent 5 modulo 6. Wir haben ein Differenzenmuster 4, 2, 4, 2, 4, 2, ... . Damit kann induktiv gezeigt werden, dass die Summen aufeinanderfolgender solcher Zahlen die Vielfachen von 6 ergeben.