Hans Walser, [20090410b]
Siebeneck und Neuneck
Nach Ideen von J. N.
NŠherungskonstruktionen auf der Basis eines Quadratrasters.
1 Eine NŠherungskonstruktion des Siebeneckes
Wir arbeiten in einem
quadratischen 
-Raster gemŠ§ Figur.
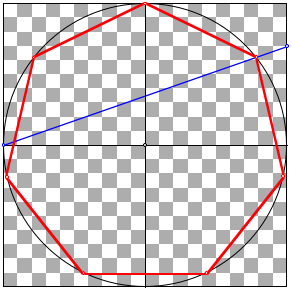
NŠherungskonstruktion des Siebeneckes
Wir schneiden den Umkreis mit der blauen Geraden und erhalten so einen Eckpunkt.
Wie genau ist diese Konstruktion?
Bearbeitung
Bezeichnungen gemŠ§ Figur.
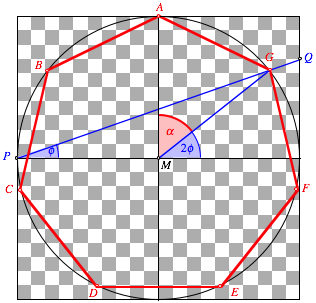
Bezeichnungen
Die
Gerade PQ hat die Steigung 
und damit den
Steigungswinkel 
. Damit gilt fŸr den Sektorwinkel 
:
Der
exakte Wert wŠre 
.
2 NŠhrungskonstruktionen des Neuneckes
2.1 Sehr genaue NŠherungskonstruktion
Wir
arbeiten in einem quadratischen 
-Raster gemŠ§ Figur.
NŠherungskonstruktion des Neuneckes
Beschreibung
Bezeichnungen gemŠ§ Figur.
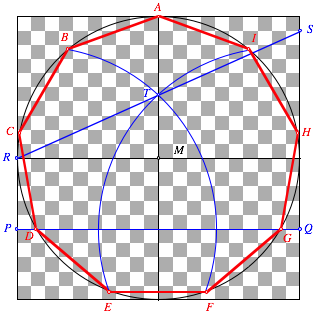
Bezeichnungen
Wir schneiden den Umkreis mit der Gitterlinie PQ und erhalten D und G. Diese Punkte bilden zusammen mit A ein exaktes gleichseitiges Dreieck. Sie sind also auch fŸr das Neuneck exakt. Nun mŸssten die 120¡-Winkel mit Scheitel M gedrittelt werden, dies geht aber nicht mit Zirkel und Lineal.
Ab hier also NŠherungskonstruktion. Wir Konstruieren den Punkt T gemŠ§ Figur und zeichnen dann Kreise um D und G durch T. Schnitt mit dem Umkreis ergibt nŠherungsweise die Eckpunkte B, F, E, I.
Die
Punkte C und H erhalten wir Ÿber die Winkelhalbierenden von 
und 
.
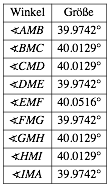
Genauigkeit: Die Sektorwinkel mit Scheitel M mŸssten alle 40¡ messen. TatsŠchlich ist aber:
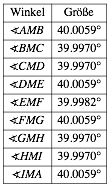
2.2 Etwas gršbere NŠherungskonstruktion
Wir
arbeiten in einem quadratischen 
-Raster gemŠ§ Figur.
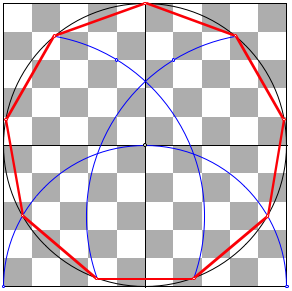
NŠherungskonstruktion des Neuneckes
Beschreibung
Bezeichnungen gemŠ§ Figur.
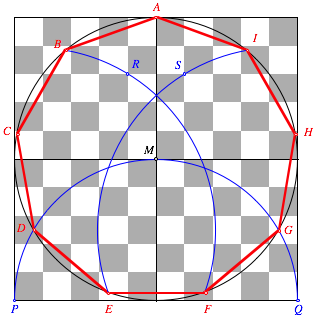
Bezeichnungen
ZunŠchst
zeichnen wir mit dem Halbkreis PMQ
die beiden Punkte D und G. Diese Punkte bilden zusammen mit A ein exaktes gleichseitiges Dreieck.
Sie sind also auch fŸr das Neuneck exakt. Nun zeichnen wir die beiden Kreise um
D und G durch die respektiven Rasterpunkte R und S. Schnitt mit dem
Umkreis ergibt nŠherungsweise die Eckpunkte B,
F, E, I. Die Punkte C und H erhalten wir Ÿber die
Winkelhalbierenden von 
und 
.
Genauigkeit: Die Sektorwinkel mit Scheitel M mŸssten alle 40¡ messen. TatsŠchlich ist aber:
