Hans Walser, [20170512]

Sierpiński-Fraktale

Anregungen: A. K., V. und O. R., T.

1 Worum geht es?

Aus Ähnlichkeits-Puzzles mit Vierer-Unterteilung werden Fraktale analog zum bekannten Sierpiński-Dreieck gebaut.

Ein Ähnlichkeitspuzzle mit Vierer-Unterteilung (ad hoc Bezeichnung) ist eine Figur, die sich in vier kongruente zur Ausgangsfigur ähnliche Teilfiguren zerlegen lässt. Naheliegende Beispiele sind das beliebige Dreieck und das Parallelogramm. Ich habe keine Übersicht über alle möglichen Beispiele. Dies ist ein separates Thema. Vgl. (Hemme 1989).

Die Idee ist, von den vier Teilfiguren bei der Fraktalisierung jeweils eine auszusparen.

Es werden einige Beispiele vorgestellt. Es gibt noch viele andere Beispiele.

2 Erinnerung: Sierpiński-Dreieck

Die Abbildung 1a zeigt das gleichseitige Dreieck als Ähnlichkeitspuzzle und das zugehörige Sierpiński-Dreieck.

Es wird jeweils das Dreieck in der Mitte ausgespart (Abb. 1b).

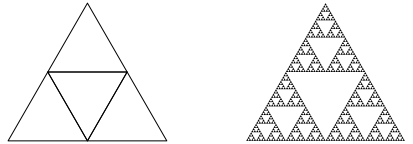
Abb. 1a: Sierpiński-Dreieck

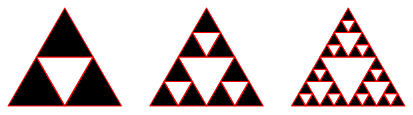
Abb. 1b: Die ersten drei Schritte

3 Beispiele

3.1 Im regulären Dreiecksraster

3.1.1 60°-Rhombus

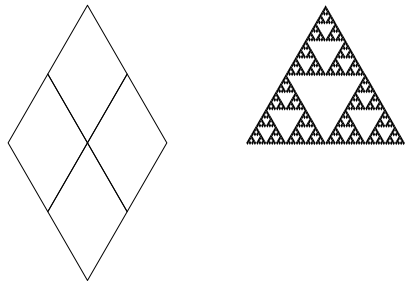
Abb. 2a: 60°-Rhombus als Ausgangsfigur

Wir erhalten wieder das Sierpiński-Dreieck.

Die Abbildung 2b zeigt die ersten drei Schritte der Fraktalisierung. Es wird jeweils der unterste Rhombus ausgespart.

Abb. 2a: Die ersten drei Schritte

3.1.2 Trapez

3.1.2.1 Bekannte Grundfigur

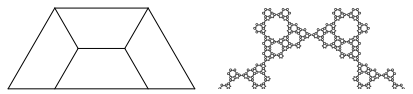
Abb. 3a: Trapez-Puzzle und Fraktal

Die Abbildung 3a illustriert die ersten Schritte für das Fraktal. Es wird jeweils das Trapez unten Mitte ausgespart.

Abb. 3a: Die ersten drei Schritte

3.1.2.2 Variante

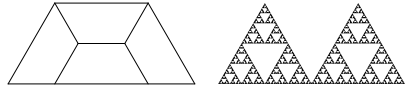
Abb. 4a: Sterzinsky-Zwillinge

Die Abbildung 4b zeigt die ersten Schritte dieser Variante. Es wird jeweils das Trapez oben Mitte ausgespart.

Abb. 4b: Die ersten drei Schritte

3.1.2.3 Weitere Variante

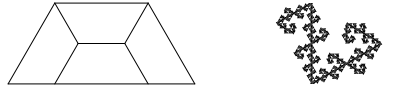
Abb. 5a: Weitere Variante

Die Abbildung 5b zeigt die ersten Schritte dieser Variante. Es wird jeweils das Trapez links ausgespart.

Abb. 5b: Die ersten drei Schritte

3.1.3 Asymmetrisches Beispiel

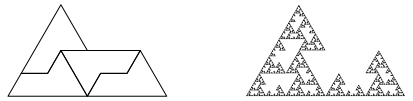
Abb. 6a: Asymmetrisches Beispiel

Abb. 6b: Die ersten drei Schritte

3.1.4 Versteckte gleichseitige Dreiecke

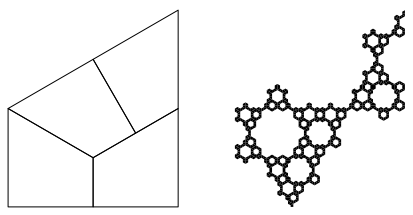
Abb. 7a: Andere Grundfigur

Das Fraktal ist verwandt mit dem Fraktal der Abbildung 3a.

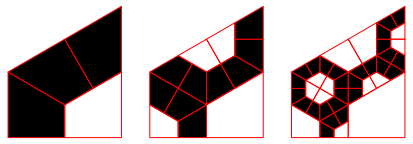
Abb. 7b: Die ersten drei Schritte

Weitere Varianten seien den geneigten Leser/innen überlassen.

3.2 Im Quadratraster

3.2.1 Dreiviertelquadrat

3.2.1.1 An der konkaven Ecke ausgespart

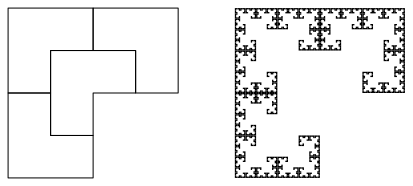
Abb. 8a: Dreiviertelquadrat

Auch das ist in der Grundform ein alter Bekannter. Die Abbildung 8b zeigt die ersten Schritte. Es wird das innerste Dreiviertelquadrat ausgespart.

Abb. 8b: Die ersten drei Schritte

3.2.1.2 Links oben ausgespart

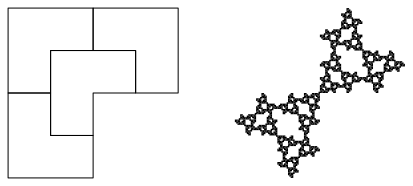
Abb.9a: Variante zum Dreiviertelquadrat

Abb. 9b: Die ersten drei Schritte

3.2.2 Pfanne

3.2.2.1 An der konkaven Ecke ausgespart

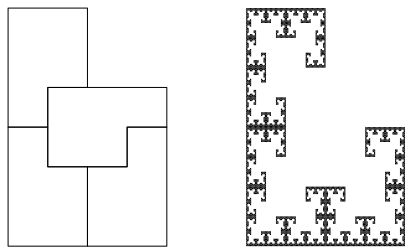
Abb. 10a: Pfanne

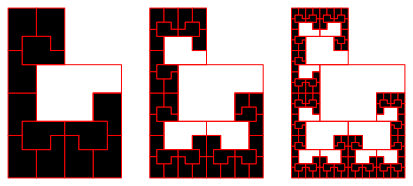
Abb. 10b: Die ersten drei Schritte

3.2.2.2 Links unten ausgespart

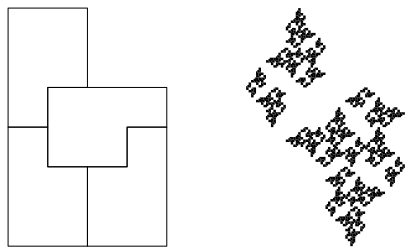
Abb. 11a: Variante

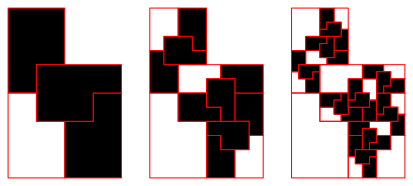
Abb. 11b: Die ersten drei Schritte

3.2.3 45°-Winkel

3.2.3.1 Ausgangslage

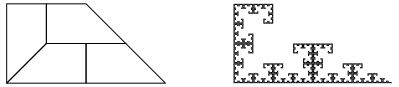
Abb. 12a: Trapeze mit 45°-Winkeln

Abb. 12b: Die ersten drei Schritte

3.2.3.2 Variante

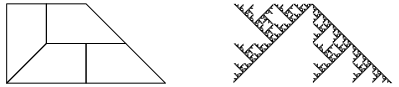
Abb. 13a: Variante

Abb. 13b: Die drei ersten Schritte

3.2.4 Halbes Quadrat

3.2.4.1 Links unten ausgespart

Abb. 14a: Halbes Quadrat

Abb. 14b: Die ersten drei Schritte

3.2.4.2 Links oben ausgespart

Abb. 15a: Variante

Abb. 15b: Die ersten drei Schritte

3.2.5 2×1-Rechteck

3.2.5.1 Die simple Tour

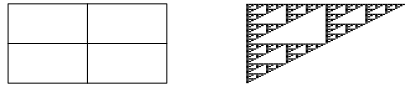
Abb. 16: Affiner Gruß vom Sierpiński-Dreieck

Abb. 16b: Die ersten drei Schritte

3.2.5.2 Folge

Abb. 17a: Folge

Abb. 17b: Die ersten drei Schritte

3.2.5.3 Das zweite Rechteck ausgespart

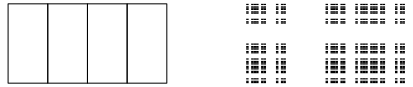
Abb. 18a: Asymmetrischer Cantor-Staub

Abb. 18b: Die ersten drei Schritte

3.2.5.4 Innen quer

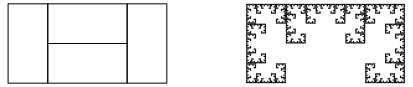
Abb. 19a: Innenhöfe

Abb. 19b: Die ersten drei Schritte

3.2.5.5 Variante

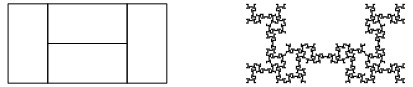
Abb. 20a: Innen- und Außenhöfe

Abb. 20b: Die drei ersten Schritte

3.2.6 Ein L

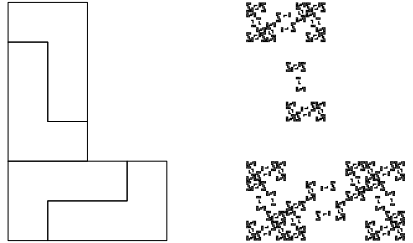
Abb. 21a: L

Abb. 21b: Die ersten drei Schritte

3.2.7 Quadrat

3.2.7.1 Sierpiński

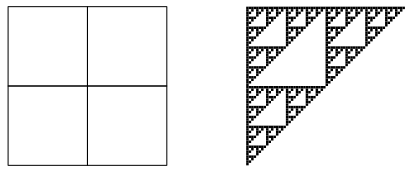
Abb. 21a: Schon wieder das Sierpiński-Dreieck

Abb. 21b: Die drei ersten Schritte

3.2.7.2 Variante

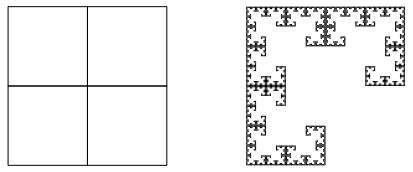
Abb. 22a: Alter Bekannter (Abb. 8)

Abb. 22b: Die ersten drei Schritte

3.2.7.3 Noch eine Variante

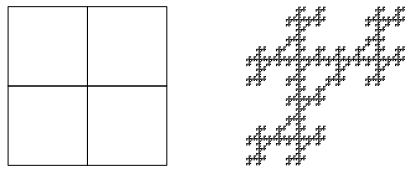
Abb. 23a: Noch eine Variante

Abb. 23b: Die ersten drei Schritte

3.2.7.4 Und noch eine Variante

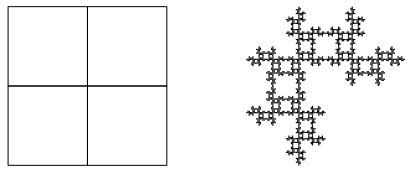
Abb. 24a: Und noch eine Variante

Abb. 24b: Die drei ersten Schritte

4 Fraktale Dimension

Sämtliche Beispiele haben dieselbe fraktale Dimension D, nämlich:

(1)

Literatur

Hemme, Heinrich (1989): Geometrische Gerüchte: Figuren, die sich selbst vervielfachen. bild der wissenschaft, 5-1989. 141-144.

Mandelbrot, Benoît B. (1983). The Fractal Geometry of Nature. New York: Freeman. ISBN 0-7167-1186-9

Mandelbrot, Benoît B. (1991). Die fraktale Geometrie der Natur. Basel: Birkhäuser.