Hans Walser, [20230120]

Sierpiński-T

Anregung: Thomas Jahre, Aufgabe 62 -737

1 Worum geht es?

Zerlegungsproblem. Analogie zum Sierpiński-Dreieck

2 Aufgabenstellung

In ein Quadratgitter zeichnen wir ein aus fünf Quadraten zusammengesetztes T (Abb. 1).

Abb. 1: T

Dieses T soll in 4, 16, 64, ... , 4ⁿ kongruente Teilfiguren zerlegt werden.

3 Lösung

Abb. 2: Lösung

4 Der Witz der Sache

Ein Einzelteil der Unterteilung lässt sich seinerseits in vier kongruente und zur Ausgangsfigur ähnliche Teile zerlegen (Abb. 3).

Abb. 3: Unterteilung einer Teilfigur

Durch Iteration dieser Zerlegung kommen wir zu den Figuren der Abbildung 2.

5 Fraktalisierung

Die Idee ist, von den vier Teilfiguren jeweils eine wegzulassen. Ich habe jeweils die in der Abbildung 4 grün markierte Teilfigur weggelassen.

Abb. 4: Weglassen einer Teilfigur

Die Abbildung 5 illustriert den Fraktalisierungsprozess.

Abb. 5: Fraktalisierung

Entsprechend kommen wir zum Sierpiński-T (Abb. 6).

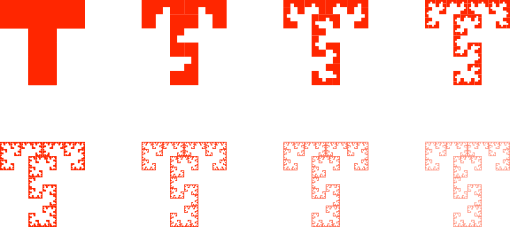
Abb. 6: Sierpiński-T

6 Variante

Wir lassen jeweils die grün markierte Teilfigur gemäß der Abbildung 7 weg.

Abb. 7: Weglassen einer anderen Teilfigur

Die Abbildung 8 illustriert den nun zugehörigen Fraktalisierungsprozess.

Abb. 8: Fraktalisierung

Entsprechend das Sierpiński-T (Abb. 9).

Abb. 9: Anderes Sierpiński-T

Weblinks

Thomas Jahre, Aufgabe 62 – 737

https://www.schulmodell.eu/aufgabe-der-woche.html

Hans Walser: Iterationen

http://www.walser-h-m.ch/hans/Miniaturen/I/Iterationen/Iterationen.html

Hans Walser: Iterationen

http://www.walser-h-m.ch/hans/Miniaturen/I/Iterationen2/Iterationen2.html

Hans Walser: Goldener Schnitt

http://www.walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_7/Goldener_Schnitt_7.html