Hans Walser, [20160410], [20220112], [20220916]
Simplex
1 Worum geht es?
Ein Simplex oder n-Simplex ist das n-dimensionale Analogon zu Strecke, Dreieck, Tetraeder, ... .
Wir
setzen die Kantenlänge 1 voraus (regelmäßiges Simplex) und berechnen die Höhe 
und das n-d-Volumen 
sowie weiteres.
Die Abbildung 1 zeigt ein regelmäßiges Tetraeder.
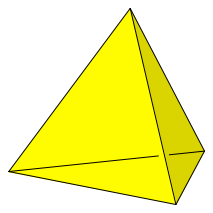
Abb. 1: Regelmäßiges Tetraeder
2 Höhe
Aus der Schule bekannt:
(1)
Es gilt die Rekursion:
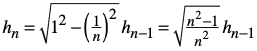(2)
Explizite Formel:
(3)
Beweis induktiv: Wegen (1) ok für n = 1. Induktionsschritt:
(4)
Die Tabelle 1 gibt die ersten 50 Werte.
|
n |
hn |
hn |
|
n |
hn |
hn |
|
1 |
1 |
1 |
|
26 |
3/26*39^(1/2) |
0.7205766922 |
|
2 |
1/2*3^(1/2) |
0.8660254040 |
|
27 |
1/9*42^(1/2) |
0.7200822997 |
|
3 |
1/3*6^(1/2) |
0.8164965809 |
|
28 |
1/28*406^(1/2) |
0.7196229171 |
|
4 |
1/4*10^(1/2) |
0.7905694150 |
|
29 |
1/29*435^(1/2) |
0.7191949521 |
|
5 |
1/5*15^(1/2) |
0.7745966692 |
|
30 |
1/30*465^(1/2) |
0.7187952883 |
|
6 |
1/6*21^(1/2) |
0.7637626160 |
|
31 |
4/31*31^(1/2) |
0.7184212083 |
|
7 |
2/7*7^(1/2) |
0.7559289460 |
|
32 |
1/8*33^(1/2) |
0.7180703309 |
|
8 |
3/4 |
0.75 |
|
33 |
1/33*561^(1/2) |
0.7177405624 |
|
9 |
1/3*5^(1/2) |
0.7453559923 |
|
34 |
1/34*595^(1/2) |
0.7174300542 |
|
10 |
1/10*55^(1/2) |
0.7416198487 |
|
35 |
3/35*70^(1/2) |
0.7171371655 |
|
11 |
1/11*66^(1/2) |
0.7385489459 |
|
36 |
1/12*74^(1/2) |
0.7168604389 |
|
12 |
1/12*78^(1/2) |
0.7359800721 |
|
37 |
1/37*703^(1/2) |
0.7165985722 |
|
13 |
1/13*91^(1/2) |
0.7337993857 |
|
38 |
1/38*741^(1/2) |
0.7163503994 |
|
14 |
1/14*105^(1/2) |
0.7319250550 |
|
39 |
2/39*195^(1/2) |
0.7161148738 |
|
15 |
2/15*30^(1/2) |
0.7302967432 |
|
40 |
1/20*205^(1/2) |
0.7158910530 |
|
16 |
1/8*34^(1/2) |
0.7288689869 |
|
41 |
1/41*861^(1/2) |
0.7156780853 |
|
17 |
3/17*17^(1/2) |
0.7276068750 |
|
42 |
1/42*903^(1/2) |
0.7154752000 |
|
18 |
1/6*19^(1/2) |
0.7264831575 |
|
43 |
1/43*946^(1/2) |
0.7152816976 |
|
19 |
1/19*190^(1/2) |
0.7254762500 |
|
44 |
3/44*110^(1/2) |
0.7150969418 |
|
20 |
1/20*210^(1/2) |
0.7245688375 |
|
45 |
1/15*115^(1/2) |
0.7149203527 |
|
21 |
1/21*231^(1/2) |
0.7237468643 |
|
46 |
1/46*1081^(1/2) |
0.7147514009 |
|
22 |
1/22*253^(1/2) |
0.7229988054 |
|
47 |
2/47*282^(1/2) |
0.7145896009 |
|
23 |
2/23*69^(1/2) |
0.7223151185 |
|
48 |
7/24*6^(1/2) |
0.7144345085 |
|
24 |
5/12*3^(1/2) |
0.7216878367 |
|
49 |
5/7 |
0.7142857143 |
|
25 |
1/5*13^(1/2) |
0.7211102550 |
|
50 |
1/10*51^(1/2) |
0.7141428429 |
Tab. 1: Erste Werte
Die Werte hn sind rational für n = 1, 8, 49 (gelb unterlegt). Für n ≤ 10.000.000 gibt es die rationalen Werte hn der Tabelle 2.
|
n |
hn rational |
|
1 |
1 |
|
8 |
3/4 |
|
49 |
5/7 |
|
288 |
17/24 |
|
1681 |
29/41 |
|
9800 |
99/140 |
|
57121 |
169/239 |
|
332928 |
577/816 |
|
1940449 |
985/1393 |
Tab. 2: Rationale Werte
Grenzwert: Es ist:
(5)
Die Höhen haben eine untere Schranke.
3 Volumen
Aus der Schule bekannt:
(6)
Rekursion (Verwendung von (3)):
(7)
Explizite Formel:
(8)
Beweis induktiv: Wegen (6) ok für n = 1. Induktionsschritt:
(9)
Grenzwert: Es ist:
(10)
Das Volumen verschwindet sehr rasch (Tab. 3).
|
n |
|
|
1 |
1 |
|
2 |
0.4330127020 |
|
3 |
0.1178511302 |
|
4 |
0.02329237477 |
|
5 |
0.003608439184 |
|
6 |
0.0004593318248 |
|
7 |
0.00004960317460 |
|
8 |
0.000004650297621 |
Tab. 3: Das Volumen verschwindet
4 Bauteile
Wir erstellen eine Tabelle (Tab. 4) über die Anzahl der Eckpunkte, der Kanten, der Dreiecke, der Tetraeder, allgemein der niedrigerdimensionalen „Seitenelemente“ des n-Simplexes.
In der
Kopfzeile die Dimension 
der Bauteile,
in der linken Spalte die Dimension n
des Simplex. Den Punkt bezeichnen wir als 0-Simplex. Den n-Simplex zählen wir bei seiner eigenen Dimension einmal mit.
|
n\k |
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
1 |
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
2 |
3 |
3 |
1 |
|
|
|
|
3 |
4 |
6 |
4 |
1 |
|
|
|
4 |
5 |
10 |
10 |
5 |
1 |
|
|
5 |
6 |
15 |
20 |
15 |
6 |
1 |
Tab. 4: Bauteile
Wir erkennen das Pascal-Dreieck der Binomialkoeffizienten, wobei die Spalte ganz links fehlt.
Zum Verständnis stellen wir uns den Übergang von einer Dimension in die nächste vor: Es kommt ein zusätzlicher Eckpunkt ins Spiel, der mit allen bisherigen Bauteilen verbunden wird. Zu den schon vorhandenen Dreiecken zum Beispiel kommen zusätzlich alle Dreiecke, die mit dem neuen Eckpunkt und den bisherigen Kanten gebildet werden können. Mit dieser Überlegung ergibt sich die übliche Rekursion für das Pascal-Dreieck.
Man
beachte den Versatz bei der Indizierung: Das n-Simplex hat 
Eckpunkte.
5 Gesamte Kantenlänge
Das n-Simplex hat
Kanten der Länge eins.
Die
Anzahl ist also auch die gesamte Kantenlänge. Die Kantenlänge divergiert für 
.
6 Gesamte Hyperoberfläche
Das n–Simplex hat n + 1 Simplexe der Dimension n – 1 als Hyperoberflächenelemente. Für die gesamte Hyperoberfläche erhalten wir daher:
(11)
Wir
erhalten für 
den Grenzwert
null (Tab. 5).
|
n |
Hyperoberfläche |
|
1 |
2 |
|
2 |
3 |
|
3 |
1.732050808 |
|
4 |
0.5892556510 |
|
5 |
0.1397542486 |
|
6 |
0.02525907427 |
|
7 |
0.003674654599 |
|
8 |
0.0004464285713 |
|
9 |
0.00004650297621 |
|
10 |
0.000004236377687 |
Tab. 5: Hyperoberfläche
Obwohl die Kantenlänge divergiert, gehen Volumen und Hyperoberfläche gegen null. Eine recht spießige Sache.
7 Gesamte 2-d-Fläche
Das n-Simplex hat
gleichseitige
Dreiecke mit dem Flächeninhalt 
. Die gesamte 2-d-Fläche divergiert also.
Analog kann gezeigt werden, dass bei festem k das gesamte k-dim-Hypervolumen divergiert.
Wenn wir also in der Tabelle 2 senkrecht nach unten gehen, divergiert es.
8 Gesamte n–2-dim Hyperfläche
Das n-Simplex hat
Bauelemente der Dimension n – 2. Für die Summe deren Hypervolumina erhalten wir:
(12)
Auch dies geht gegen null (Tab. 6, Lesebeispiele: Das Dreieck (n = 2) hat drei Ecken. Das Tetraeder (n = 3) hat die gesamte Kantenlänge 6. Die gleichseitigen Dreiecke im 4-Simplex haben die Gesamtfläche 4.330127020):
|
n |
n–2-Unterhypervolumina |
|
2 |
3 |
|
3 |
6 |
|
4 |
4.330127020 |
|
5 |
1.767766953 |
|
6 |
0.4891398700 |
|
7 |
0.1010362971 |
|
8 |
0.01653594569 |
|
9 |
0.002232142857 |
|
10 |
0.0002557663690 |
Tab. 6: Unterdach
Allgemein ist es so, dass wir bei Schrägen parallel zur rechten Kante des Pascal-Dreiecks den Grenzwert null erhalten. Schuld sind die Fakultäten im Nenner. Dagegen ist kein Kraut gewachsen.
9 Kartesisches Koordinatensystem
Wir betten das n-dimensionale Simplex A0A1...An in ein kartesisches x1,x2,...,xn-Koordinatensystem ein gemäß Abbildung 2. Die Idee dabei ist, dass jedes k-dimensionale Untersimplex A0A1...Ak im Teil-Koordinatensystem mit den x1,x2,...,xk-Achsen beschrieben werden kann.
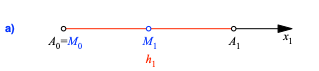
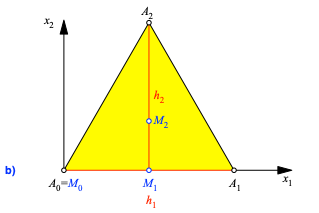
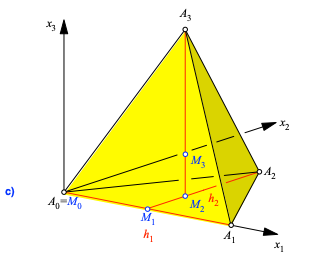
Abb. 2: Kartesisches Koordinatensystem
Die Eckpunkte Ak, im Folgenden mit A[k] bezeichnet, haben die Koordinaten:
A[0] := [ seq(0, j = 1 .. n) ]:
for k from 1 to n do
A[k] := [seq(1/(j+1)*h[j], j = 1 .. k-1), h[k], seq(0, j = k+1 .. n)]:
end:
Die Tabelle 7 gibt die Eckpunktkoordinaten für die Dimension 5.
|
A[k] |
Koordinaten |
||||
|
A[0] |
0 |
0 |
0 |
0 |
0 |
|
A[1] |
1 |
0 |
0 |
0 |
0 |
|
A[2] |
1/2 |
1/2*3^(1/2) |
0 |
0 |
0 |
|
A[3] |
1/2 |
1/6*3^(1/2) |
1/3*6^(1/2) |
0 |
0 |
|
A[4] |
1/2 |
1/6*3^(1/2) |
1/12*6^(1/2) |
1/4*10^(1/2) |
0 |
|
A[5] |
1/2 |
1/6*3^(1/2) |
1/12*6^(1/2) |
1/20*10^(1/2) |
1/5*15^(1/2) |
Tab. 7: Eckpunktkoordinaten
Weiter sei M[k] der Mittelpunkt (Schwerpunkt) des k-dimensionale Untersimplex A0A1...Ak. Wir erhalten dafür die Koordinaten:
M[0] := [ seq(0, j = 1 .. n) ]:
for k from 1 to n do
M[k] := [seq(1/(j+1)*h[j], j = 1 .. k), seq(0,
j = k+1 .. n)]:
end:
Die Tabelle 8 gibt die Mittelpunktkoordinaten bis zur Dimension 5.
|
M[k] |
Koordinaten |
||||
|
M[0] |
0 |
0 |
0 |
0 |
0 |
|
M[1] |
1/2 |
0 |
0 |
0 |
0 |
|
M[2] |
1/2 |
1/6*3^(1/2) |
0 |
0 |
0 |
|
M[3] |
1/2 |
1/6*3^(1/2) |
1/12*6^(1/2) |
0 |
0 |
|
M[4] |
1/2 |
1/6*3^(1/2) |
1/12*6^(1/2) |
1/20*10^(1/2) |
0 |
|
M[5] |
1/2 |
1/6*3^(1/2) |
1/12*6^(1/2) |
1/20*10^(1/2) |
1/30*15^(1/2) |
Tab. 8: Mittelpunktkoordinaten
Die Abbildung 3 zeigt zur Kontrolle das nach obigen Formeln generierte dreidimensionale Tetraeder. Es stimmt mit dem Tetraeder der Abbildung 2c überein.
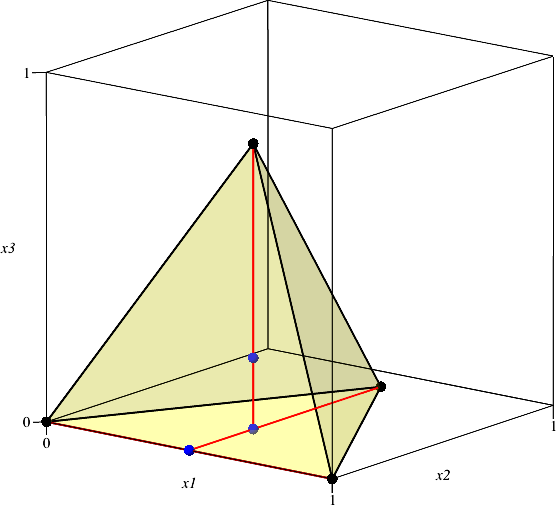
Abb. 3: Kontrollbild
10 Zentriwinkel
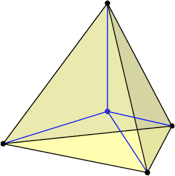
Abb. 4: Vom Mittelpunkt zu den Ecken
Wir zeichnen im Tetraeder die Strecken vom Mittelpunkt zu den Ecken (Abb. 4). Aus Symmetriegründen schließen diese Strecken paarweise denselben Winkel ein. Dies gilt auch im n-dimensionalen Fall.
Wir berechnen im gleichschenkligen Dreieck A0A1Mn den Winkel an der Spitze Mn. Das Dreieck hat die Schenkellänge
(13)
und die Basislänge 1. Mit dem Kosinussatz erhält man für den gesuchten Winkel:
(14)
Die Tabelle 9 gibt die ersten Werte.
|
n |
Zentriwinkel |
Bogenmaß |
Degree |
Bemerkung |
|
1 |
π |
3.141592654 |
180 |
„Schöner Winkel“ |
|
2 |
2/3*π |
2.094395103 |
120 |
„Schöner Winkel“ |
|
3 |
arccos(–1/3) |
1.910633237 |
109.4712207 |
Schnittwinkel der Würfeldiagonalen |
|
4 |
arccos(–1/4) |
1.823476582 |
104.4775122 |
|
|
5 |
arccos(–1/5) |
1.772154248 |
101.5369590 |
|
|
6 |
arccos(–1/6) |
1.738244406 |
99.59406822 |
|
|
7 |
arccos(–1/7) |
1.714143896 |
98.21321071 |
|
|
8 |
arccos(–1/8) |
1.696124158 |
97.18075577 |
|
|
9 |
arccos(–1/9) |
1.682137342 |
96.37937024 |
|
|
10 |
arccos(–1/10) |
1.670963748 |
95.73917047 |
|
Tab. 9: Zentriwinkel
Für wachsende n strebt der Zentriwinkel gegen den rechten Winkel.
Weblinks
Hans Walser: Verallgemeinerung des Satzes von Pythagoras
http://www.walser-h-m.ch/hans/Miniaturen/V/Verallg_Pythagoras2/Verallg_Pythagoras2.htm