Hans Walser, [20220925]
Simplex
1 Worum geht es?
Darstellung des nd-Simplex (nd-Hypertetraeder) im Kontext des nd-Hyperwürfels
2 Vorgehen
Die Abbildung 1
illustriert das Vorgehen für das Tetraeder im dreidimensionalen Würfel.
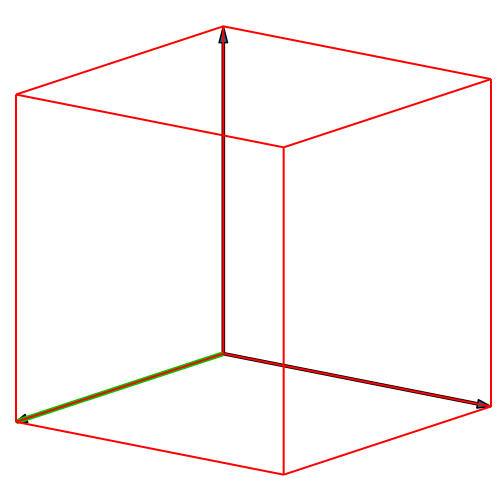
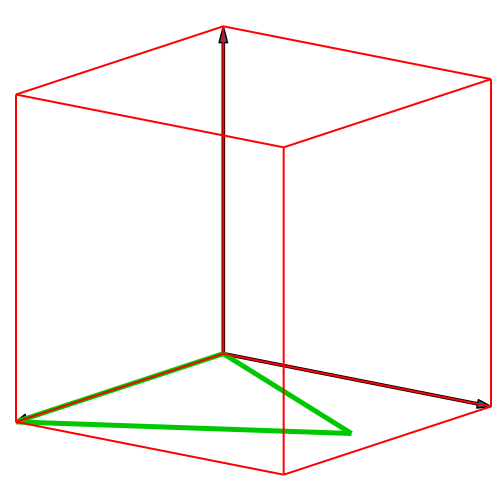
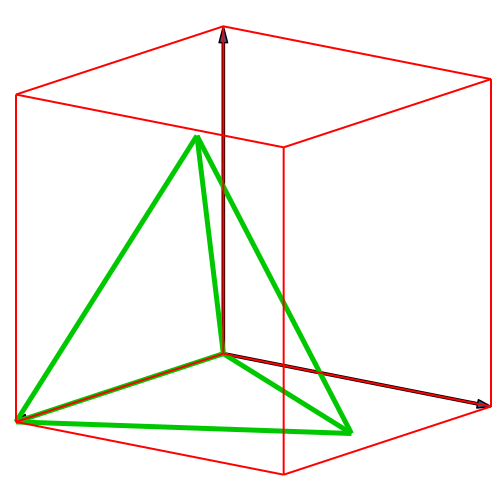
Abb. 1:
Konstruktion des Tetraeders im Würfel
Die Abbildung 3
zeigt eine andere Sicht desselben Vorganges.
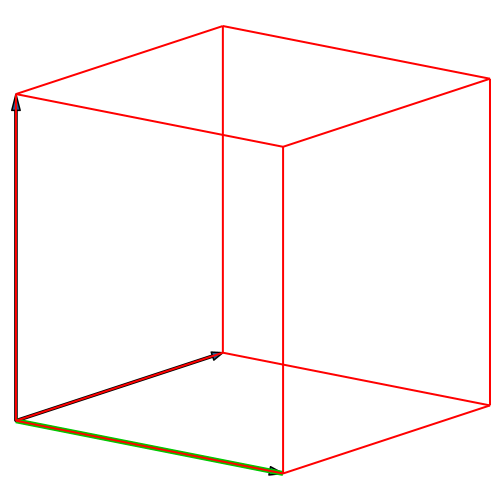
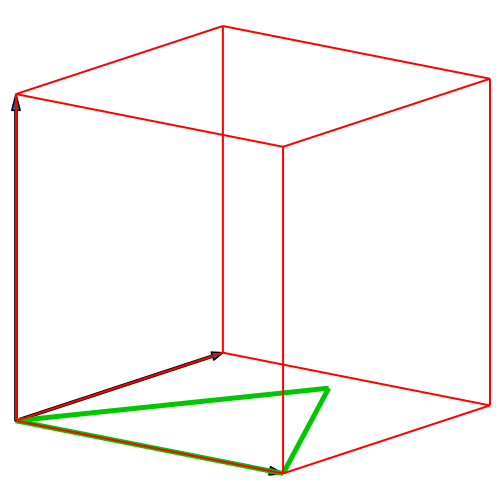
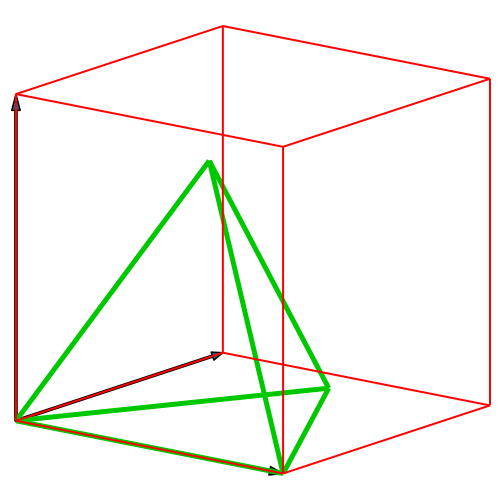
Abb. 2: Andere
Sicht
In der Abbildung 3
ist der Würfel in isometrischer Darstellung gezeichnet. Die Schlussfigur
irritiert etwas. Die Frage ist, ob das grüne (scheinbare) Dreieck in der
Schlussfigur gleichseitig ist (ist nicht der Fall, ist nicht einmal ein Dreieck,
sondern ein Tetraeder).
Die drei
Basisvektoren sind sternförmig angeordnet. Daher bezeichnen wir diese
Darstellung als Stern-Darstellung.
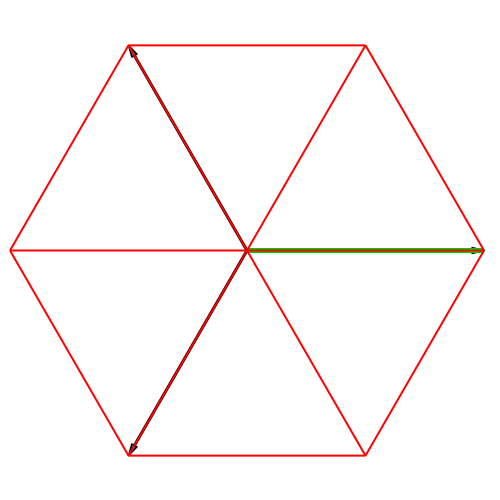
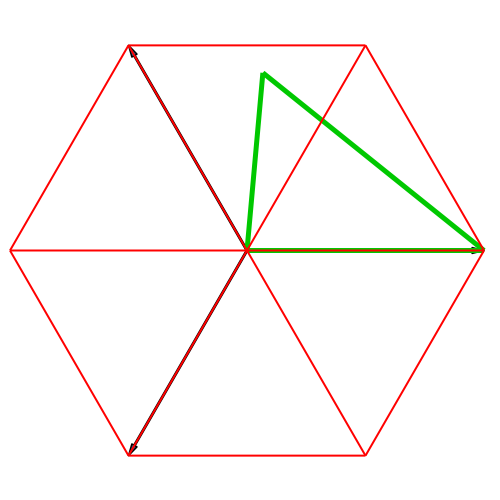
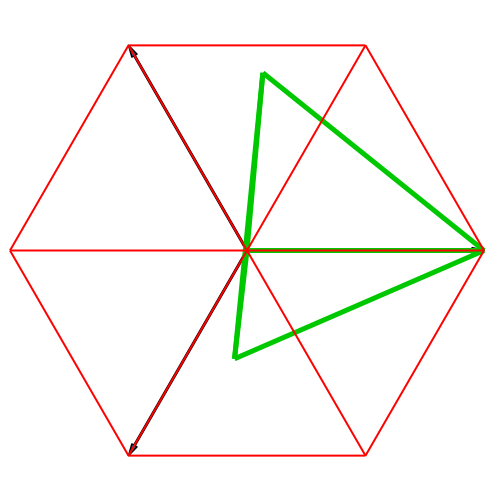
Abb. 3:
Isometrische Darstellung
In der Abbildung 4
sind die Basisvektoren fächerförmig angeordnet. Daher Fächer-Darstellung.
Hier stellt sich die Frage, ob das grüne Viereck in der Schlussfigur ein
Drachenviereck ist (ist nicht der Fall).
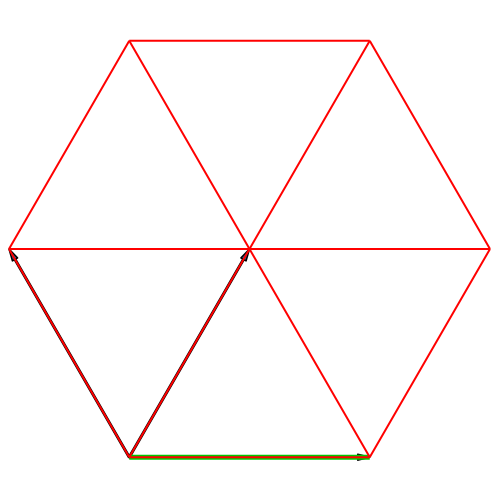
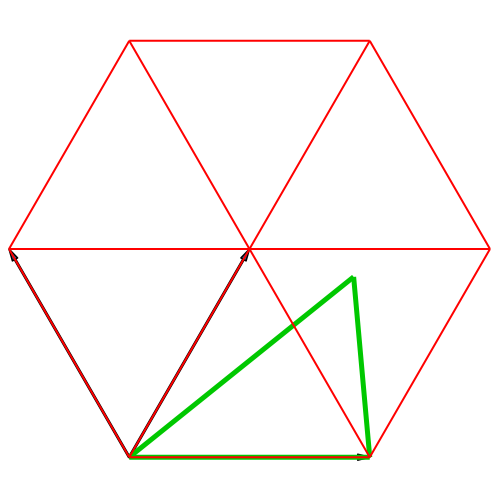
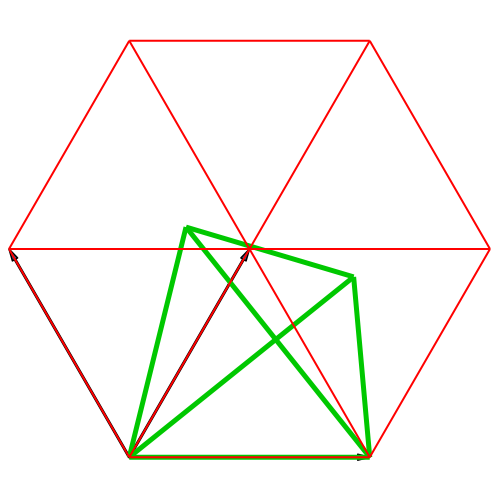
Abb. 4:
Isometrische Fächer-Darstellung
3
Im
vierdimensionalen Hyperwürfel
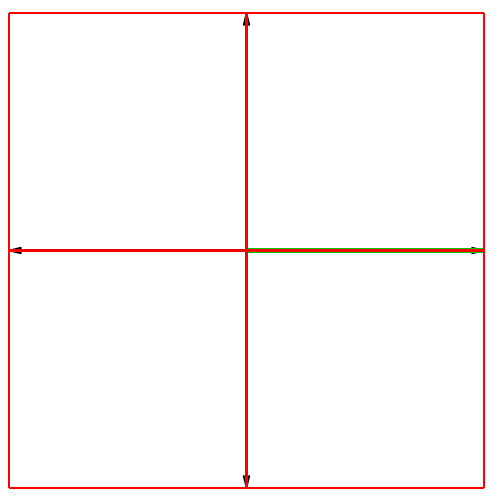
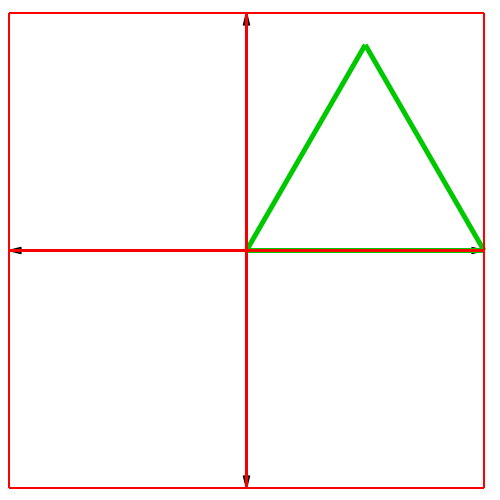

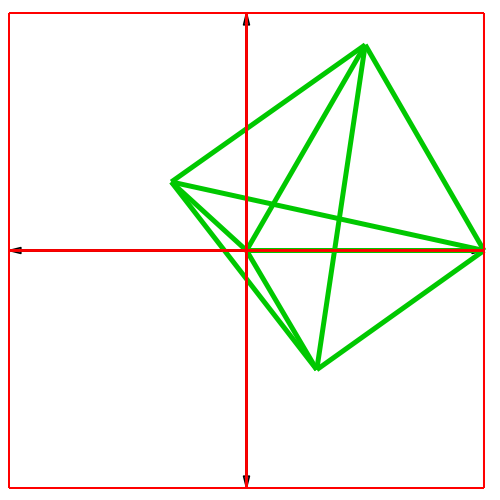
Abb. 5:
Isometrische Stern-Darstellung
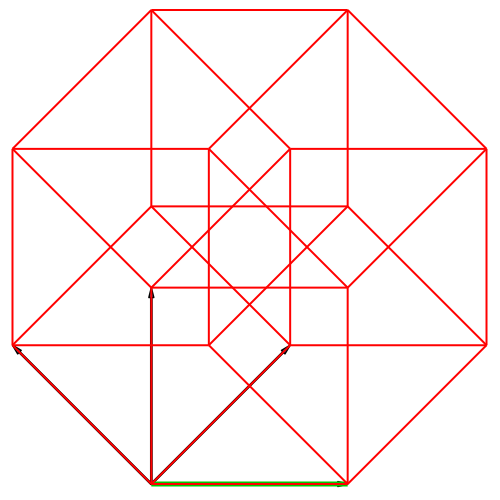
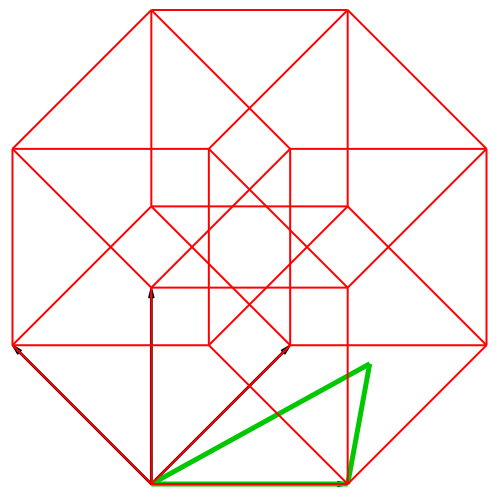
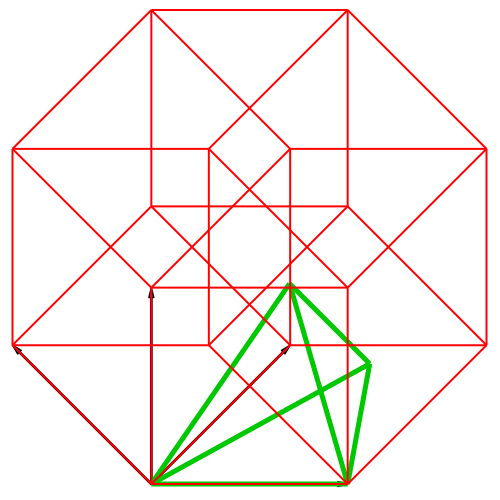
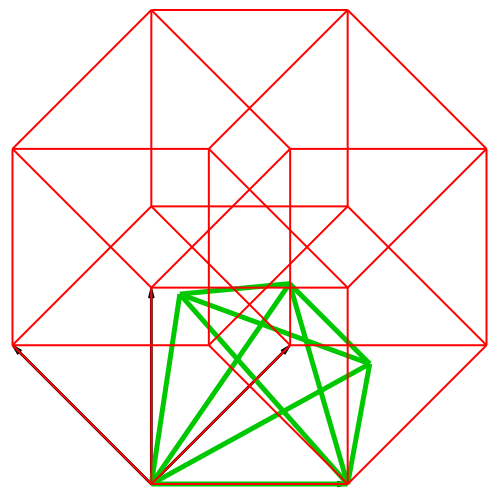
Abb.
6: Fächer-Darstellung
4 Weitere Beispiele
In den folgenden Beispielen
wird die Schlussfigur (nd-Simplex im nd-Hyperwürfel) je in der Stern-Darstellung und in der
Fächer-Darstellung gegeben.
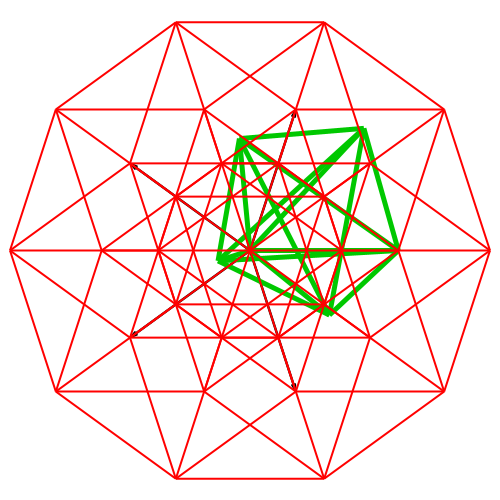
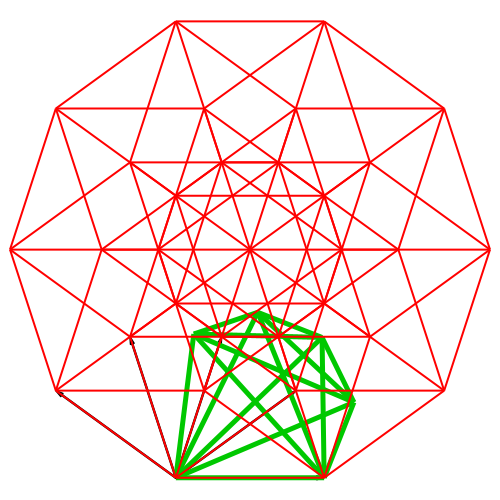
Abb. 7:
Dimension 5
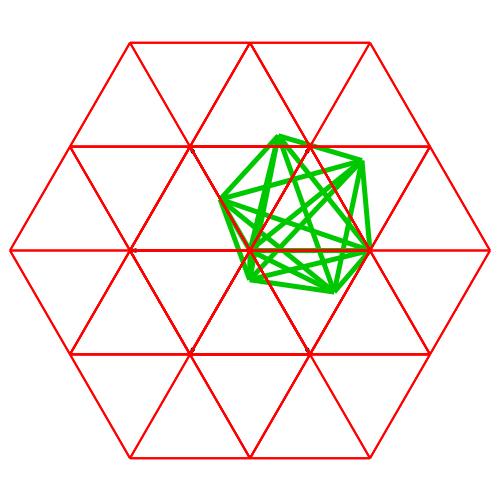
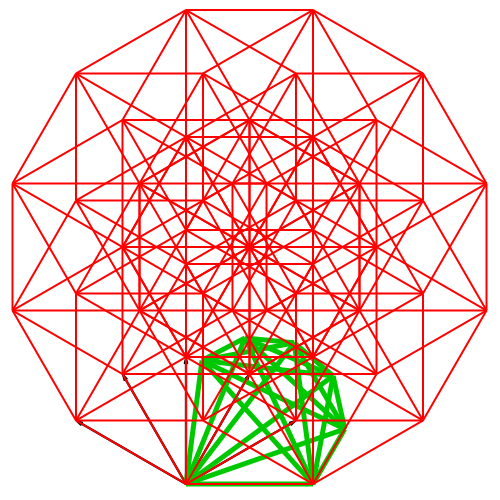
Abb. 8:
Dimension 6
Weblinks
Hans Walser: Simplex
http://www.walser-h-m.ch/hans/Miniaturen/S/Simplex/Simplex.htm
Hans Walser: Verallgemeinerung des Satzes von Pythagoras
http://www.walser-h-m.ch/hans/Miniaturen/V/Verallg_Pythagoras2/Verallg_Pythagoras2.htm