1 Problemstellung

Gesucht ist eine nichttriviale Skala so dass jede Streckenlänge 1, 2, 3, 4, … durch zwei der Skalenmarken entstehen kann.

Die triviale Skala ist der Zahlenstrahl mit den Marken 0, 1, 2, 3, 4, … .

2 Eine Lösung

Wir unterteilen einen Kreis in 1 + 2 + 4 = 7 Teile (Abb. 1). Die Zahl 7 ist die Summe der ersten drei Zweierpotenzen: 2⁰ + 2¹ + 2² = 7.

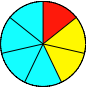
Abb. 1: Unterteilung des Kreises

Auf dem Rand können wir zunächst die Bogenlängen 1, 2, 3, 4, 5, 6 und 7 generieren (Abb. 2).

Abb. 2: Bogenlängen 1 bis 7

Mit der Bogenlänge 8 kommen wir in Schwierigkeiten. Das Boot ist voll.

Wir behelfen uns, indem wir die runde Skala der Abbildung 1 abwickeln, und das gleich mehrfach (so oft wie benötigt) (Abb. 3).

Abb. 3: Abwicklung der Skala

Nun geht es. Die Abbildung 4 zeigt die ersten 21 Streckenlängen.

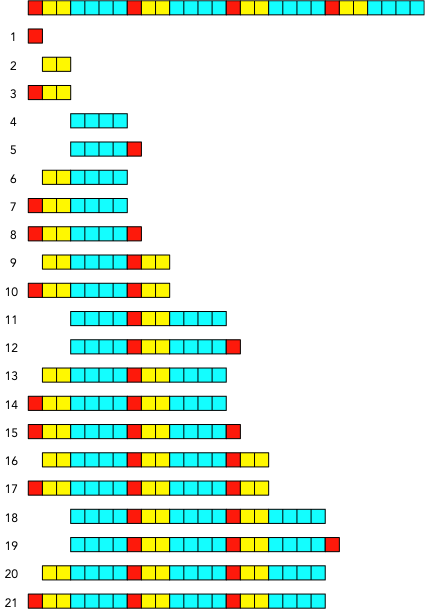
Abb. 4: Streckenlängen

Wir sehen, wie der Hase läuft. Induktiv kann bewiesen werden, dass es für jede Streckenlänge 1, 2, 3, 4, … geht. Beim Induktionsbeweis muss modulo 7 gearbeitet werden.

3 Die einfachste nichttriviale Lösung

Wir arbeiten mit den beiden ersten Zweierpotenzen: 2⁰ + 2¹ = 1 + 2 = 3 (Abb. 5).

Abb. 5: 1 + 2 = 3

Die Abbildung 6 zeigt die Abwicklung.

Abb. 6: Abwicklung

Die Abbildung 7 zeigt die ersten 12 Streckenlängen.

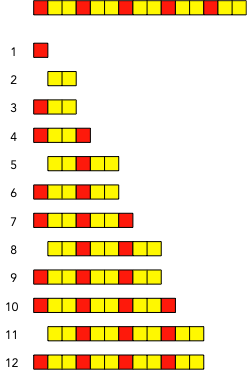
Abb. 7: Streckenlängen

Auch hier kann induktiv bewiesen werden, dass es für alle Streckenlängen funktioniert.

4 Was leider nicht geht

Die Sache ist nicht aufwärtskompatibel. Für 2⁰ + 2¹ + 2² + 2³= 1+ 2 + 4 + 8 = 15 geht es mit der Streckenlänge 5 nicht. Das liegt daran, dass die 1 und die 4 nicht nebeneinander liegen.

Somit gibt es nur die beiden oben beschriebenen nichttrivialen Lösungen.

Website

Thomas Jahre: Chemnitzer Schulmodell

https://www.schulmodell.eu/aufgabe-der-woche.html