Hans Walser, [20171002]
Spezielle Ellipsen
1 Worum geht es?
Konjugierte Ellipsen, bei denen die Brennpunkte der einen Ellipse jeweils auf der andren Ellipse liegen, vgl. [1].
2 Zwei Ellipsen
Gesucht ist das Achsenverhltnis der Ellipsen der Abbildung 1. Die Brennpunkte jeder Ellipse liegen jeweils auf der anderen Ellipse.
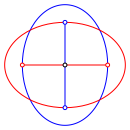
Abb. 1: Spezielle Ellipsen
Das
Achsenverhltnis ist ![]() .
.
3 Drei Ellipsen
Gesucht sind drei kongruente Ellipsen, deren Brennpunkte jeweils auf den beiden anderen Ellipsen liegen. Gesucht sind die Achsen a und b der Ellipsen.
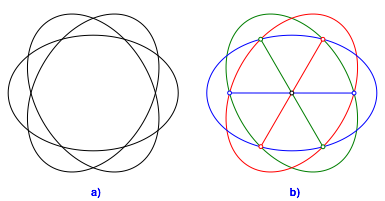
Abb. 2: Drei Ellipsen
Das Zentrum und die sechs Brennpunkte bilden ein regulres Dreiecksraster, dessen Seitenlnge wir 1 setzen.
Damit ist:
![]() (1)
(1)
Der Punkt
mit den Koordinaten ![]() liegt auf
der Ellipse mit der Gleichung:
liegt auf
der Ellipse mit der Gleichung:
![]() (2)
(2)
Es ist also:
![]() (3)
(3)
Aus (1) und (3) ergibt sich eine biquadratische Gleichung fr a. Die positiven reellen Lsungen sind:
![]() und
und ![]() (4)
(4)
Fr das Achsenverhltnis ergibt sich:
![]() (5)
(5)
4 Vier Ellipsen
Gesucht sind vier kongruente Ellipsen, deren Brennpunkte jeweils auf den beiden benachbarten Ellipsen liegen (Abb. 3).
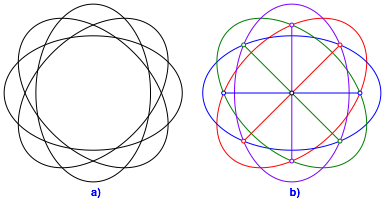
Abb. 3: Vier Ellipsen
Man beachte, dass zum Beispiel die Brennpunkte der roten Ellipse (Abb. 3b) nicht auf der grnen Ellipse liegen. Rot und grn sind also nicht konjugiert.
Fr die
Berechnung von a und b setzen wir die halbe Brennpunktweite c = 1. Damit gilt wieder die Gleichung
(1). Die Ellipse mit der Gleichung (2) verluft durch den Punkt mit den Koordinaten ![]() . Somit erhalten wir die Bedingung:
. Somit erhalten wir die Bedingung:
![]() (6)
(6)
Die Gleichungen (1) und (6) ergeben eine biquadratische Gleichung fr a mit den positiven reellen Lsungen:
![]() (7)
(7)
5 Allgemein
Gesucht sind n ³ 2 kongruente Ellipsen, deren Brennpunkte jeweils auf den beiden benachbarten Ellipsen liegen. Die Abbildung 4 zeigt die Situation fr n = 12.
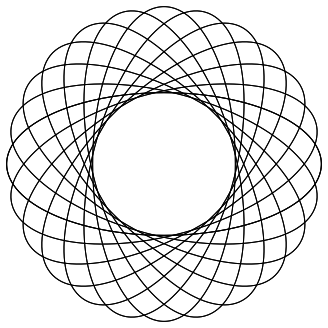
Abb. 4: Zwlf Ellipsen
Fr die
Berechnung von a und b setzen wir die halbe Brennpunktweite c = 1. Damit gilt wieder die Gleichung
(1). Die Ellipse mit der Gleichung (2) verluft durch den Punkt mit den Koordinaten ![]() . Somit erhalten wir die Bedingung:
. Somit erhalten wir die Bedingung:
![]() (8)
(8)
Die Tabelle 1 gibt die positiven reellen Lsungen in Abhngigkeit von n.
|
n |
a |
b |
|
2 |
1.414213562 |
1 |
|
3 |
1.366025404 |
0.9306048592 |
|
4 |
1.306562965 |
0.8408964155 |
|
5 |
1.260073511 |
0.7666715415 |
|
6 |
1.224744872 |
0.7071067810 |
|
7 |
1.197448846 |
0.6586985192 |
|
8 |
1.175875602 |
0.6186141224 |
|
9 |
1.158455931 |
0.5848248826 |
|
10 |
1.144122805 |
0.5558929702 |
|
11 |
1.132136280 |
0.5307848499 |
|
12 |
1.121971054 |
0.5087426116 |
Tab. 1: Numerische Werte
Websites
[1] Konjugierte Kegelschnitte (abgerufen 01.10.2017):
http://www.walser-h-m.ch/hans/Miniaturen/K/Konjugierte_Kegelschnitte/Konjugierte_Kegelschnitte.htm