Hans Walser, [20131216a], [20140308]
SphŠrische Spiralen
1 Idee
Die Idee ist einfach: Wir zeichnen auf einer Weltkarte eine schrŠg ansteigende Gerade und studieren deren Bild auf der Kugel.
Je nach Kartentyp gibt das verschiedene Kurven auf der Kugel.
2 Plattkarte
In der Plattkarte ist das Gradnetz ein Quadratnetz. Die Karte der Abbildung 1 hat eine Maschenweite von 15¡.
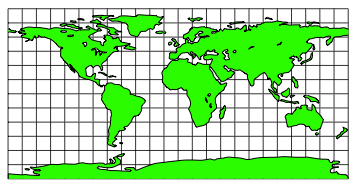
Abb. 1: Plattkarte
2.1 Steigung 1
Die Geraden mit Steigung ±1 folgen den Diagonalen der Netzquadrate (Abb. 2).
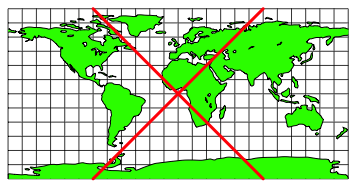
Abb. 2: Situation auf der Karte
Die Abbildung 3 zeigt die Situation auf der Kugel. Die Kurve wird als vivianische Kurve oder Strophoide bezeichnet.
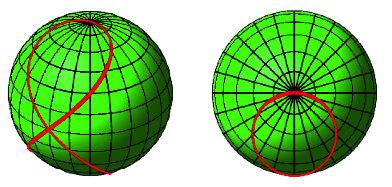
Abb. 3: Situation auf der Kugel
Wenn wir die Sache von oben ansehen, erscheint ein Kreis. TatsŠchlich ist die Kurve die Schnittkurve der Kugel mit einem stehenden Kreis-Zylinder (Abb. 4).
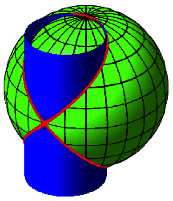
Abb. 4: Schnitt mit Kreis-Zylinder
2.2 Steigung 2
Die Steigung ±2 berechnen wir aus der Sicht der SŸd-Nord-Achse. Die primŠre Variable ist also die geografische Breite. Auf ein Karo in SŸd-Nord-Reichung geht es ±2 Karos in West-Ost-Richtung.
Die Steigung ±2
entspricht der ãgewšhnlichenÒ Steigung 
(Abb. 5).
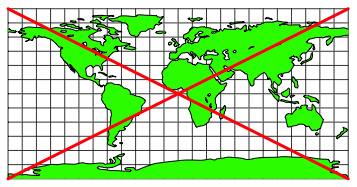
Abb. 5: Steigung ±2
Auf der Kugel ergibt sich eine herzfšrmige Kurve (Abb. 6).
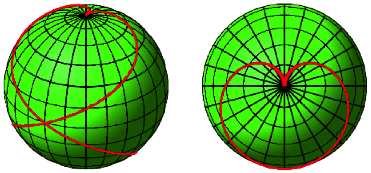
Abb. 6: Steigung ±2
Die Sicht von oben ist aber nicht die Kardioide. In der Abbildung 7 ist unserer Kurve (rot) die Kardioide (blau) gegenŸbergestellt.
Abb. 7: Vergleich mit Kardioide
NatŸrlich kšnnen wir auch hier mit einem Zylinder arbeiten. Er hat die rote Kurve als Leitlinie (Abb. 8).
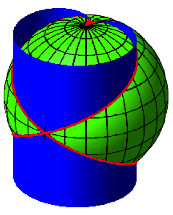
Abb. 8: Zylinder
2.3 Steigung 4
Bei der Steigung 4 muss die Kurve zweimal in West-Ost-Richtung die Erde umkreisen, um den Weg vom SŸdpol zum Nordpol zu schaffen (Abb. 9).
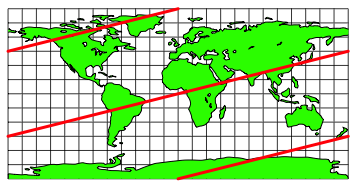
Abb. 9: Steigung 4
Wenn wir die Plattkarte zum Zylinder aufwickeln, erhalten wir eine Schraubenlinie.
Auf der Erdkugel ist die doppelte Erdumkreisung ebenfalls zu erahnen (Abb. 10). Es entwickelt sich eine Doppelspirale mit Zentren in den beiden Polen.
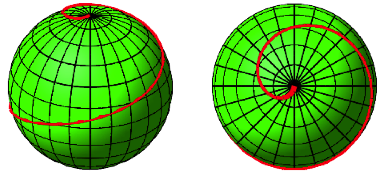
Abb. 10: Steigung 4
2.4 Steigung 24
Die Abbildung 11 zeigt in der Plalttkarte die Situation fŸr die Steigung 24.
Abb. 11: Steigung 24
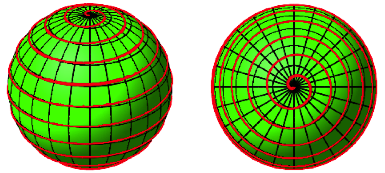
Abb. 12: Spirale auf der Kugel
Bei diesen Spiralen wŠchst die Poldistanz pro Umgang immer um denselben Betrag; bei der Steigung 24 sind es 15¡. Diese Spiralen sind also ein sphŠrisches Analogon zu den archimedischen Spiralen.
FŸr die Steigung a haben diese Spiralen die Parameterdarstellung:
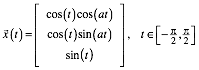
Daraus ergibt sich 
und fŸr die
BogenlŠnge s von Pol zu Pol:
Dieses Integral kann von
Maple nur numerisch gelšst werden. FŸr 
ergibt sich zum
Beispiel:
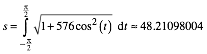
3 Mercator-Karte
Die Mercator-Karte ist winkeltreu. Die Abbildung 13 zeigt die Mercator-Karte fŸr eine Maschenweite 15¡. Das Gradnetz erscheint auf der Karte nicht mehr als Quadratnetz. Die Karte reicht auch nicht bis zu den Polen, denn diese sind auf der Mercator-Karte im Unendlichen.
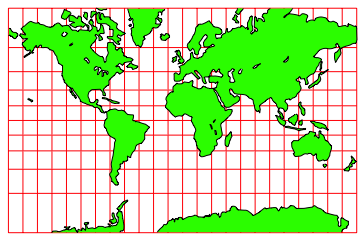
Abb. 13: Mercator-Karte
Wir kšnnen aber der Karte ein Quadratnetz unterlegen (Abb. 14).
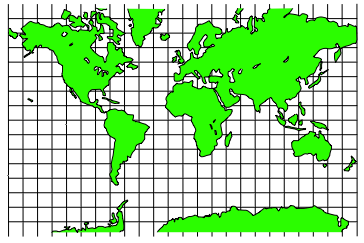
Abb. 14: Quadratnetz in der Mercator-Karte
Die senkrechten Linien des Quadratnetzes stimmen mit den Meridianen der Karte Ÿberein. Bei den horizontalen Linien stimmt es aber nur am €quator. Das Quadratnetz ist willkŸrlich oben und unten bei ±¹ abgeschnitten worden. Dies ist nicht bei den Polen.
Nun bilden wir dieses Quadratnetz auf die Kugel ab (Abb. 15).
Abb. 15: Quadratnetz auf Kugel
Die Maschenweite nimmt in Richtung der Pole ab. Es gibt sogar unendlich viele Quadrate bis zu den Polen.
Nun zeichnen wir wieder Geraden in die Karte und bilden diese auf die Kugel ab.
3.1 Steigung 1
Die Gerade hat die Richtung der Quadratdiagonalen.
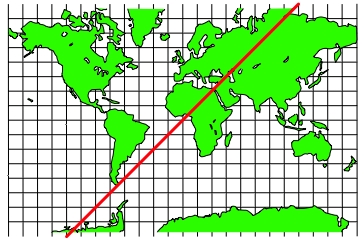
Abb. 16: Steigung 1 auf Mercator-Karte
Auf der Kugel entsteht eine so genannte Loxodrome (Abb. 17).
Loxodromen haben gegenŸber der Nordrichtung immer denselben Kurswinkel, in unserem Beispiel ist das 45¡E. Wir sehen, wie die Kurve den Quadratdiagonalen entlang lŠuft.
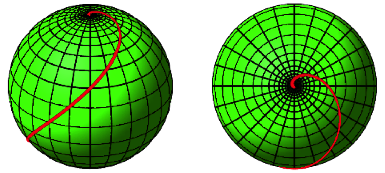
Abb. 17: Loxodrome
3.2 Steigung 2
Bei der Steigung 2 sehen wir, dass es mehrere UmgŠnge braucht. Da die Mercator-Karte an sich oben und unten ins Unendliche geht, braucht es sogar unendlich viele UmgŠnge, um von Pol zu Pol zu gelangen.
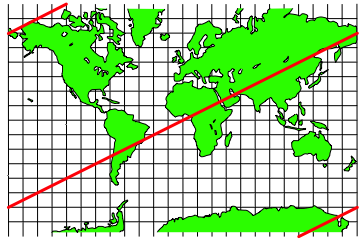
Abb. 18: Steigung 2 auf der Mercator Karte
Auf der Kugel erhalten
wir die Loxodrome zum Kurswinkel 
(Abb. 19).
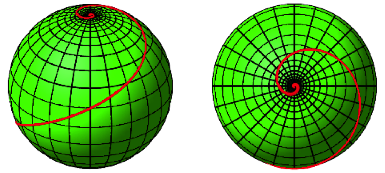
Abb. 19: Loxodrome mit Steigung 2
Solche Loxodromen hat M.C. Escher als Grundlage fŸr verschiedene Grafiken verwendet.
3.3 Steigung 12
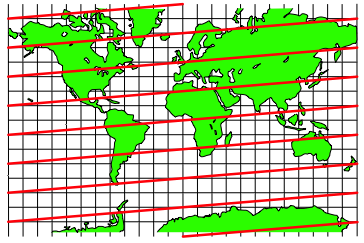
Abb. 20: Steigung 12
Abb. 21: Steigung 12
Die Loxodrome zur Steigung a hat die Parameterdarstellung:
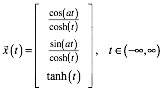
Daraus ergibt sich 
und fŸr die
BogenlŠnge s von Pol zu Pol:
Die Loxodromen sind das sphŠrische Analogon zu den logarithmischen Spiralen. Die logarithmischen Spiralen haben nŠmlich ebenfalls einen konstanten Kurswinkel zum Zentrum.
4 Karte von Archimedes/Lambert
Die Karte nach Archimedes/Lambert ist flŠchentreutreu. Die Abbildung 22 zeigt diese Karte fŸr eine Maschenweite 15¡. Das Gradnetz erscheint auf der Karte nicht mehr als Quadratnetz.
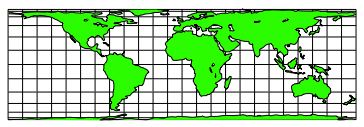
Abb. 22: FlŠchentreue Karte nach Archimedes/Lambert
Die Dimensionen dieser
Karte sind im irrationalen VerhŠltnis 
; die Karte kann daher nicht randbŸndig mit einem
Quadratraster Ÿberdeckt werden. Trotzdem kšnnen wir natŸrlich Geraden
verschiedener Steigungen einzeichnen und auf die Kugel Ÿbertragen. FŸr die
Steigung a ergibt sich auf der Kugel
eine Kurve mit der Parameterdarstellung:
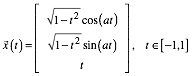
4.1 Steigung 1
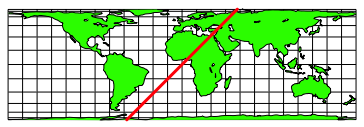
Abb. 23: Gerade mit Steigung 1
Wir erhalten auf der Kugel Kurve der Abbildung 24
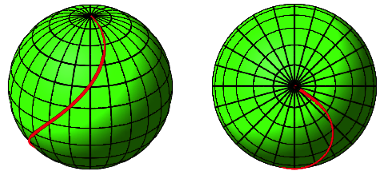
Abb. 24: Steigung 1
4.2 Steigung 2
FŸr die Steigung 2 ergibt sich die Kurve der Abbildung 25.
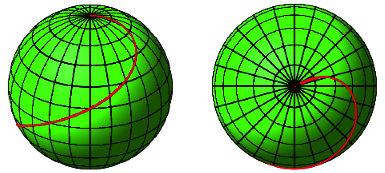
Abb. 25: Steigung 2
4.3 Steigung 24
Die Steigung 24 ergibt die Kurve der Abbildung 26.
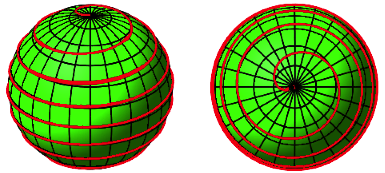
Abb. 26: Steigung 24
Ich wei§ nicht, was das ebene Analogon zu diesem Spiralentyp ist.
Das Integral
fŸr die BogenlŠnge von Pol zu Pol kann Maple nur numerisch berechnen.
4.4 Die Sinuskurve
In der Abbildung 27 ist eine Sinuskurve eingezeichnet. Sie lŠuft entlang der Diagonalen der Netzvierecke.
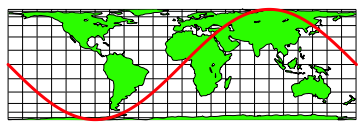
Abb. 27: Sinuskurve
Die Abbildung 28 zeigt dieselbe Kurve auf der Kugel. Es handelt sich wiederum um die vivianische Kurve oder Strophoide (Abb. 3).
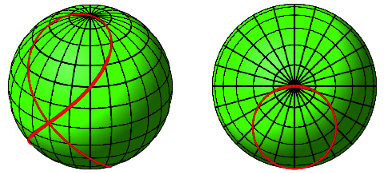
Abb. 28: Auf der Kugel