Hans Walser, [20170523a]

Sphärischer Quader

Anregung und Idee: B. K., Z.

1 Worum geht es?

Ein Quader mit dem Seitenverhältnis a : b : c wird vom Mittelpunkt aus auf die Einheitskugel projiziert.

2 Berechnungen

Maple-Programm. Die Umrechnungen in degree sind für das Funktionieren des Programms nicht erforderlich.

restart:

# Ein Quader mit dem Kantenverhaeltnis a:b:c wird vom Mittelpunkt aus auf die Einheitskugel projiziert.

a:=3; b:=4; c:=5;

# Berechnung der Seitenlaengen sx mit Skalarprodukt. Bemerkung: Die Ergaenzung von sx auf Pi ist die Diagonale dyz

sa:=evalf(arccos((-a^2 + b^2 + c^2)/(a^2 + b^2 + c^2)));

sb:=evalf(arccos((+a^2 - b^2 + c^2)/(a^2 + b^2 + c^2)));

sc:=evalf(arccos((+a^2 + b^2 - c^2)/(a^2 + b^2 + c^2)));

# Umrechnung der Seitenlaengen in degree

sad:=evalf(sa/Pi*180); sbd:=evalf(sb/Pi*180); scd:=evalf(sc/Pi*180);

# Berechnung der Winkel wx mit dem Seiten-Kosinus-Satz der sphaerischen Geometrie

wa:=arccos((-cos(sa)-cos(sb)*cos(sc))/(sin(sb)*sin(sc)));

wb:=arccos((-cos(sb)-cos(sc)*cos(sa))/(sin(sc)*sin(sa)));

wc:=arccos((-cos(sc)-cos(sa)*cos(sb))/(sin(sa)*sin(sb)));

# Kontrolle: Summe der drei Winkel muss 2*Pi sein. Sollwert: wKontrolle = 1

wKontrolle:=evalf((wa + wb + wc)/2/Pi);

# Umrechnung der Winkel in degree

wad:=evalf(wa/Pi*180); wbd:=evalf(wb/Pi*180); wcd:=evalf(wc/Pi*180);

# Berechnung der Flaechen fx mit sphaerischem Exzess

fa:=evalf(4*wa - 2*Pi); fb:=evalf(4*wb - 2*Pi); fc:=evalf(4*wc - 2*Pi);

# Kontrolle: Summe der drei Flaechen muss 2*Pi sein. Sollwert: fKontrolle = 1

fKontrolle:=evalf((fa + fb + fc)/2/Pi);

Die Abbildung 1 gibt den Ausdruck.

Abb. 1: Ausdruck

3 Grafik

Die Abbildung 2 zeigt den sphärischen Quader für a : b : c = 3 : 4 : 5.

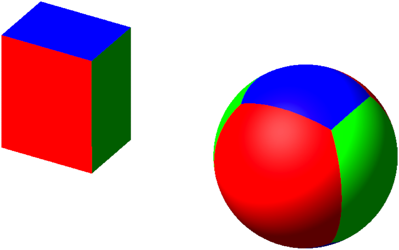
Abb. 2: Sphärischer Quader

Programm (Maple) für den sphärischen Quader:

restart: with(plots): with(plottools):

# Darstellung des sphaerischen Quaders.

a:=3; b:=4; c:=5;

# Seitenflaechen

faplus:=plot3d([a/sqrt(a^2 + u^2 + v^2), u/sqrt(a^2 + u^2 + v^2), v/sqrt(a^2 + u^2 + v^2)], u=-b..b,v=-c..c, color=red, grid=[101,101], style=surface):

faminus:=plot3d([-a/sqrt(a^2 + u^2 + v^2), u/sqrt(a^2 + u^2 + v^2), v/sqrt(a^2 + u^2 + v^2)], u=-b..b,v=-c..c, color=red, grid=[101,101], style=surface):

fbplus:=plot3d([u/sqrt(u^2 + b^2 + v^2), b/sqrt(u^2 + b^2 + v^2), v/sqrt(u^2 + b^2 + v^2)], u=-a..a,v=-c..c, color=green, grid=[101,101], style=surface):

fbminus:=plot3d([u/sqrt(u^2 + b^2 + v^2), -b/sqrt(u^2 + b^2 + v^2), v/sqrt(u^2 + b^2 + v^2)], u=-a..a,v=-c..c, color=green, grid=[101,101], style=surface):

fcplus:=plot3d([u/sqrt(u^2 + v^2 + c^2), v/sqrt(u^2 + v^2 + c^2), c/sqrt(u^2 + v^2 + c^2)], u=-a..a,v=-b..b, color=blue, grid=[101,101], style=surface):

fcminus:=plot3d([u/sqrt(u^2 + v^2 + c^2), v/sqrt(u^2 + v^2 + c^2), -c/sqrt(u^2 + v^2 + c^2)], u=-a..a,v=-b..b, color=blue, grid=[101,101], style=surface):

# display

display({faplus, faminus, fbplus, fbminus, fcplus, fcminus}, scaling=constrained, orientation=[30,60], view=[-1..1, -1..1, -1..1], axes=none, lightmodel=light4);

4 Weitere Beispiele

4.1 Sphärischer Würfel

Abb. 3: Daten sphärischer Würfel

Bemerkungen:

Die Seiten von 70.52877934° (in der sphärischen Geometrie werden auch Seiten als Winkel aufgefasst) ist der Diederwinkel des Tetraeders oder der Schnittwinkel der Diagonalen im DIN-Rechteck.

Die Winkel von 120° sind aus Symmetriegründen trivial.

Die Abbildung 4 zeigt den sphärischen Würfel.

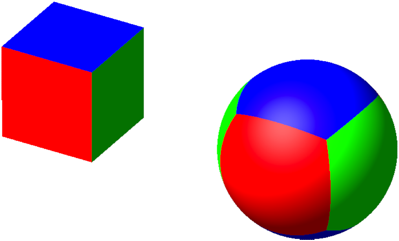
Abb. 4: Sphärischer Würfel

4.2 Großvaters Vierkantlineal

Abbildung 5 zeigt die Daten.

Abb. 5: Vierkantlineal

Die Abbildung 6 zeigt den zugehörigen sphärischen Quader. Die Rundheit der Einheitskugel leidet ein bisschen unter den extremen Daten.

Abb. 6: Das Lineal

Der Grund liegt darin, dass die Parameter u und v nicht gleichmäßig die Flächen durchlaufen. In der Abbildung 7 sind die Parameterlinien eingezeichnet (style = patch). Es gibt eine Konzentration gegen die „Pole“.

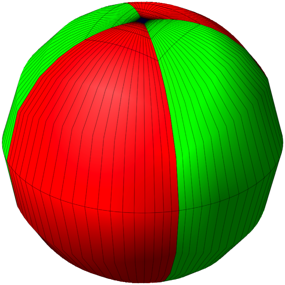
Abb. 7: Parameterlinien

Wir müssen also an den Parametern schräubeln. Nachfolgend das revidierte Programm. Die Parameter sind durch ihre Quadrate ersetzt worden, der Parameterbereich entsprechend angepasst.

restart: with(plots): with(plottools):

# Darstellung des sphaerischen Quaders.

a:=1; b:=1; c:=30;

# Seitenflaechen

faplus:=plot3d([a/sqrt(a^2 + u^4 + v^4), signum(u)*u^2/sqrt(a^2 + u^4 + v^4), signum(v)*v^2/sqrt(a^2 + u^4 + v^4)], u=-sqrt(b)..sqrt(b),v=-sqrt(c)..sqrt(c), color=red, grid=[101,101], style=patch):

faminus:=plot3d([-a/sqrt(a^2 + u^4 + v^4), signum(u)*u^2/sqrt(a^2 + u^4 + v^4), signum(v)*v^2/sqrt(a^2 + u^4 + v^4)], u=-sqrt(b)..sqrt(b),v=-sqrt(c)..sqrt(c), color=red, grid=[101,101], style=patch):

fbplus:=plot3d([signum(u)*u^2/sqrt(u^4 + b^2 + v^4), b/sqrt(u^4 + b^2 + v^4), signum(v)*v^2/sqrt(u^4 + b^2 + v^4)], u=-sqrt(a)..sqrt(a),v=-sqrt(c)..sqrt(c), color=green, grid=[101,101], style=patch):

fbminus:=plot3d([signum(u)*u^2/sqrt(u^4 + b^2 + v^4), -b/sqrt(u^4 + b^2 + v^4), signum(v)*v^2/sqrt(u^4 + b^2 + v^4)], u=-sqrt(a)..sqrt(a),v=-sqrt(c)..sqrt(c), color=green, grid=[101,101], style=patch):

fcplus:=plot3d([signum(u)*u^2/sqrt(u^4 + v^4 + c^2), signum(v)*v^2/sqrt(u^4 + v^4 + c^2), c/sqrt(u^4 + v^4 + c^2)], u=-sqrt(a)..sqrt(a),v=-sqrt(b)..sqrt(b), color=blue, grid=[101,101], style=patch):

fcminus:=plot3d([signum(u)*u^2/sqrt(u^4 + v^4 + c^2), signum(v)*v^2/sqrt(u^4 + v^4 + c^2), -c/sqrt(u^4 + v^4 + c^2)], u=-sqrt(a)..sqrt(a),v=-sqrt(b)..sqrt(b), color=blue, grid=[101,101], style=patch):

# display

display({faplus, faminus, fbplus, fbminus, fcplus, fcminus}, scaling=constrained, orientation=[30,60], view=[-1..1, -1..1, -1..1], axes=none, lightmodel=light4);

Die Abbildung 8 zeigt die etwas regelmäßiger verteilten Parameterlinien.

Abb. 8: Parameterlinien etwas ausgeglichener

Die Abbildung 9 zeigt schließlich die schöne Darstellung (style = surface).

Abb. 9: Schöne Darstellung

Das blaue Viereck ist sehr klein. Das erklärt auch, warum das Lineal, wenn es vom Schreibtisch herunterfällt, sehr selten auf der Stirnseite stehen bleibt.

Die Abbildung 9a zeigt den Vergleich mit Großvaters Lineal.

Abb. 9a: Vergleich mit Großvaters Lineal

4.3 Weitere Beispiele

4.3.1 a = 1, b = 2, c = 3

Flaeche_a = 4.05278999, Flaeche_b = 1.52509994, Flaeche_c = 0.70529534

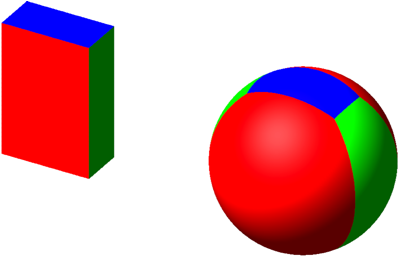
Abb. 10: Format 1:2:3

4.3.2 a = 1, b = 2, c = 4

Flaeche_a = 4.20240176, Flaeche_b = 1.64606738, Flaeche_c = 0.43471616

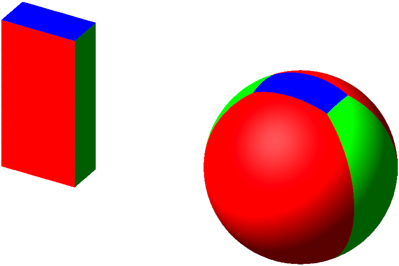
Abb. 11: Format 1:2:4

4.3.3 a = 2, b = 3, c = 4

Flaeche_a = 3.35739578, Flaeche_b = 1.83916103, Flaeche_c = 1.08662849

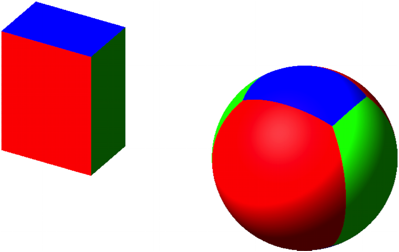
Abb. 12: Format 2:3:4