Hans Walser, [20210602]
Sphroid
1 Worum geht es?
Die Kugel hat in Grund-, Auf- und Seitenriss einen Kreis als Kontur.
Die Umkehrung gilt nicht. Es wird ein Gegenbeispiel gegeben, also ein Krper, der keine Kugel ist, aber in Grund-, Auf- und Seitenriss je einen Kreis als Kontur hat.
2 Das Sphroid
Das Sphroid (Abb. 1 und 2) ist der Durchschnitt von drei Kreiszylindern mit gleichen Radien und paarweise orthogonalen Achsen. Wir arbeiten im Folgenden mit dem Radius 1.
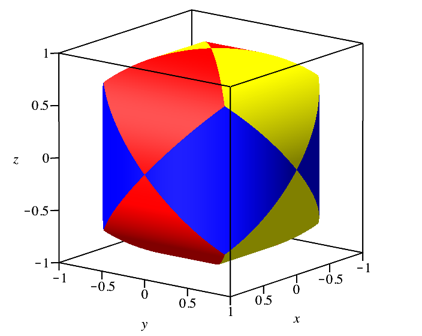
Abb. 1: Sphroid
Der gelbe Zylinder hat die x-Achse als Zylinderachse, der rote Zylinder die y-Achse und der blaue Zylinder die z-Achse. Die einzelnen Oberflchen sind abwickelbar (Abb. 8 und 9).

Abb. 2: Sphroid
3 Risse
Die Abbildung 3 zeigt Grund-, Auf- und Seitenriss. Es fllt schwer, zu glauben, dass das keine Kugel sein soll.
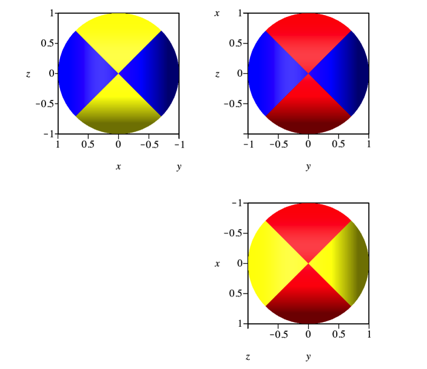
Abb. 3: Risse
4 Andere Sichten
Eine schrge Sicht (Abb. 4) macht aber deutlich, dass das keine Kugel ist. Man beachte die scheinbar verkrzten Skalierungen auf der x- und der y-Achse. Sie ergeben sich durch die schrge Sicht, Sehrichtung horizontal und mit einem Winkel 45¡ zur x-Achse. .
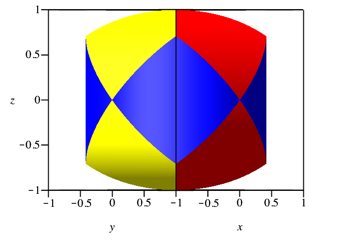
Abb. 4: Schrge Sicht
Die Figur, als zweidimensionales Bild gesehen, passt in ein Quadrat und hat einen Inkreis (Abb. 5).
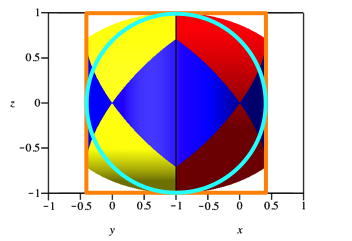
Abb. 5: Quadrat und Inkreis
5 Inkugel
In der Abbildung 6 fehlen die vier obersten gekrmmten Dreiecke, dafr ist die Inkugel eingezeichnet. Wir sehen Zwischenrume zwischen der Inkugel und dem Sphroid.
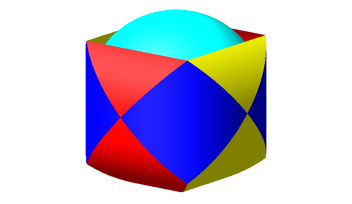
Abb. 6: Inkugel
Im Aufriss (Abb. 7) haben das Sphroid und die Inkugel dieselbe Kontur.
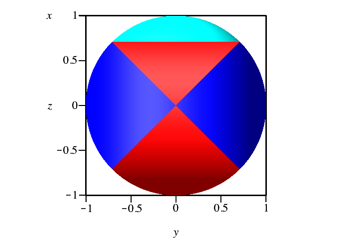
Abb. 7: Aufriss
6 Wrfel
Das
Sphroid enthlt auf seiner Oberflche die Kanten eines Wrfels (Abb. 8). Die Inkugel
des Sphroides berhrt diese Kanten in der Mitte. Die Inkugel ist die
sogenannte Kantenmittenkugel des Wrfels.
Der Wrfel hat die Kantenlnge ![]() .
.
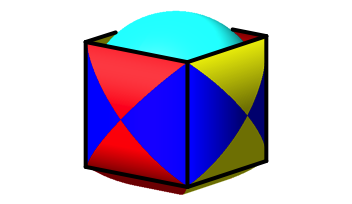
Abb. 8: Wrfelkanten auf dem Sphroid
7 Volumen und Oberflche
7.1 Kreuzgewlbe
Wir knnen umgekehrt den in der Abbildung 8 weggeschnittenen Teil als Kreuzgewlbe dem Wrfel aufsetzen (Abb. 9).
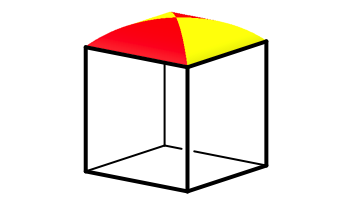
Abb. 9: Kreuzgewlbe
Die
Niveaulinien des Kreuzgewlbes sind Quadrate. Auf der vom Wrfelmittelpunt aus
gemessenen Hhe h haben diese
Quadrate die Seitenlnge ![]() . Dabei luft h
von
. Dabei luft h
von ![]() bis 1. Fr
das Volumen des Kreuzgewlbes ergibt sich damit:
bis 1. Fr
das Volumen des Kreuzgewlbes ergibt sich damit:
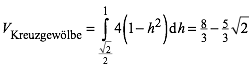
Das Sphroid setzt sich aus dem Wrfel und sechs Kreuzgewlben zusammen. Fr sein Volumen V erhalten wir daher:
![]()
7.2 Abwicklung
Die Abbildung 10 gibt die Abwicklung des Sphroides.

Abb. 10: Abwicklung
Die Randkurven der Einzelteile sind Sinus- und Kosinuskurven (Abb. 11).

Abb. 11: Randkurven
Fr die Oberflche S des Sphroides ergibt sich daher:
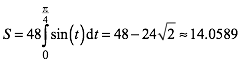
Weder
beim Volumen noch bei der Oberflche kommt die Kreiszahl ¹ vor, dafr die
ebenfalls irrationale Zahl ![]() .
.
Websitoid
Hans-Jrgen Elschenbroich: Konoid
https://www.geogebra.org/m/y57fhddh
Hans-Jrgen Elschenbroich: Konoid 2
https://www.geogebra.org/m/gqfnnhfe
Hans-Jrgen Elschenbroich: Konoidmantel
https://www.geogebra.org/m/y57fhddh
Hans Walser: Dreitafelprojektion
http://www.walser-h-m.ch/hans/Miniaturen/D/Dreitafelprojektion/Dreitafelprojektion.htm
Hans Walser: Hyperboloid-Stern
http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperboloid-Stern/Hyperboloid-Stern.htm
Hans Walser: Pyramidoid
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyramidoid/Pyramidoid.htm
Hans Walser: Paraboloid-Stern
http://www.walser-h-m.ch/hans/Miniaturen/P/Paraboloid-Stern/Paraboloid-Stern.htm
Hans Walser: Rund ohne ¹
http://www.walser-h-m.ch/hans/Miniaturen/R/Rund_ohne_Pi/Rund_ohne_Pi.htm