Hans Walser, [20200104]
Spiegeln am Viereck
1 Worum geht es?
Auflistung von PhŠnomenen. Beweise nur angedeutet.
2 Viereck
Wir beginnen mit einem Viereck ABCD in der źblichen Bezeichnungsweise (Abb. 1).
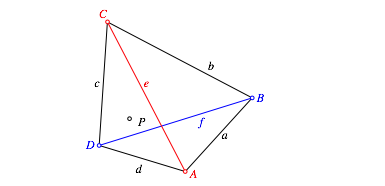
Abb. 1: Viereck
ZusŠtzlich wŠhlen wir einen Punkt P. Dieser Punkt kann beliebig sein, wenn wir ihn im Innern des Viereckes wŠhlen, werden die Folgezeichnungen źbersichtlicher.
Bemerkung: Die Frage ist, ob die folgenden †berlegungen auch spielen, wenn die Figur der Abbildung 1 als rŠumliches unregelmŠ§iges Tetraeder interpretiert wird.
3 Spiegelungen
Nun geht das gro§e Spiegeln los.
ZunŠchst
spiegeln wir den Punkt P an den vier
Seiten und an den beiden Diagonalen des Vierecks (Abb. 2). Mit 
bezeichnen
wir den an der Geraden x gespiegelten
Punkt P.
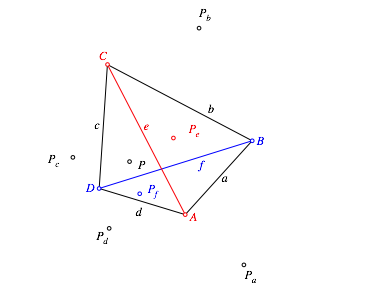
Abb. 2: Spiegeln an Geraden
Die
farbig markierten Bildpunkte spiegeln wir weiter an den gleichfarbigen
Eckpunkten des Viereckes. Mit 
bezeichnen
wir den an der Ecke Y gespiegelten
Punkt 
.
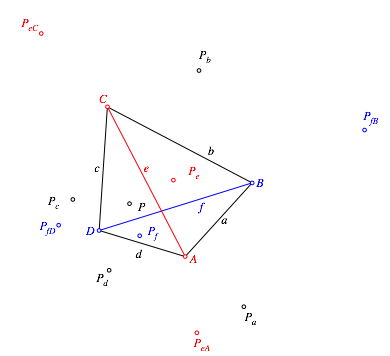
Abb. 3: Spiegeln an den Ecken
4 Parallelen
Die
Strecke 
ist
parallel zur Diagonalen e und doppelt
so lang (zentrische Streckung von 
aus) (Abb.
4). Analog ist die Strecke 
parallel
zur Diagonalen f und doppelt so lang.
Die beiden Strecken verlaufen durch den Punkt P.
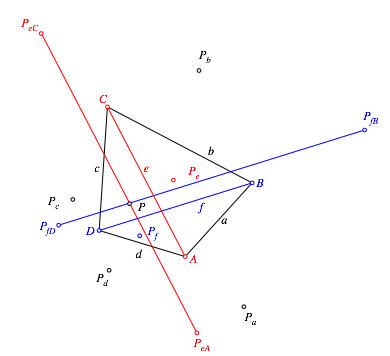
Abb. 4: Parallelen zu den Diagonalen
5 Vierecke
Wir
zeichnen nun das Viereck 
(Abb. 5).
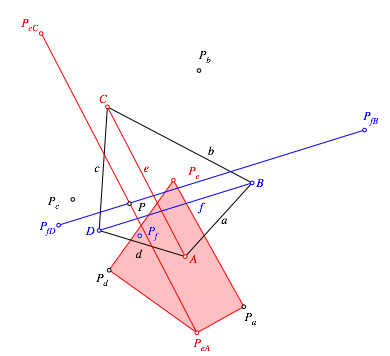
Abb. 5: Erstes Viereck
Dieses
Viereck hat rechte Winkel an den Ecken 
und 
. Es ist daher ein Sehnenviereck (Abb. 6). Der Umkreis
dieses Sehnenviereckes hat den Mittelunkt A.
Er verlŠuft durch den Punkt P. (Das allgemeine
Ausgangsviereck ABCD (Abb. 1) ist
aber kein Sehnenviereck.)
Der
Winkel an der Ecke 
ist gleich
gro§ wie der Winkel an der Ecke A des
Ausgangsviereckes.
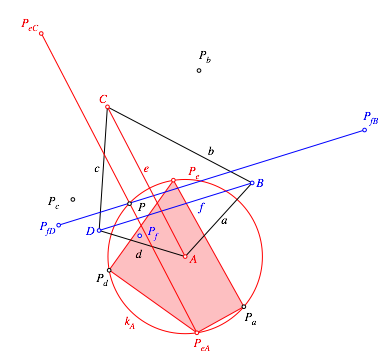
Abb. 6: Sehnenviereck
Analog kšnnen wir drei weitere Sehnenvierecke zeichnen (Abb. 7).
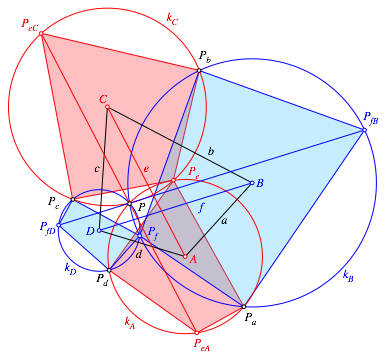
Abb. 7: Sehnenvierecke
Die Abbildung 8 zeigt die Figur ohne Beschriftung.
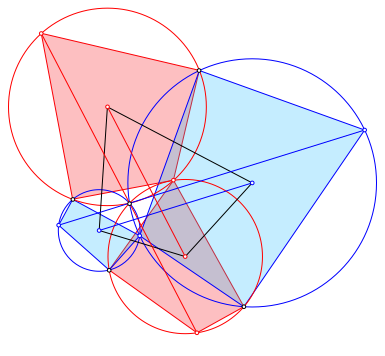
Abb. 8: Figur
6 FlŠchenornament
In der Abbildung 9 sind vier Kopien der Figur der Abbildung 8 zusammengesetzt. Zwei davon wurden punktgespiegelt. Dies ergibt die Basis eines FlŠchenornamentes.
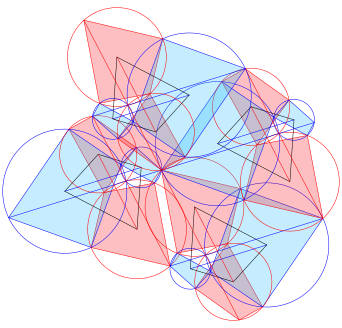
Abb. 9: FlŠchenornament, Basisteil
In der Abbildung 10 sind vier Kopien des Basisteils der Abbildung 9 zusammengesetzt.
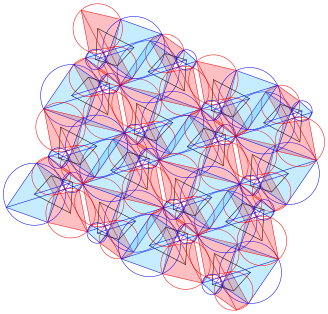
Abb. 10: FlŠchenornament
7 Winkeleigenschaft
Auf Grund der oben festgestellten Winkeleigenschaften kšnnen die Sehnenvierecke bźndig um einen Punkt herum angeordnet werden (Abb. 11).
Abb. 11: Anordnung um einen Punkt
8 Spezielle Vierecke
Wir ersetzen das allgemeine Viereck der Abbildung 1 durch spezielle Vierecke.
8.1 Parallelogramm
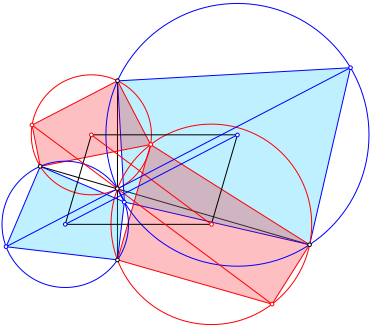
Abb. 12: Parallelogramm
Die
schwarzen Strecken (gemŠ§ Abb. 7 die Strecken 
und 
) verlaufen durch P
und sind orthogonal zu den Parallelogrammseiten. Sie sind doppelt so lang wie
die entsprechenden Hšhen des Parallelogramms.
8.2 Rhombus
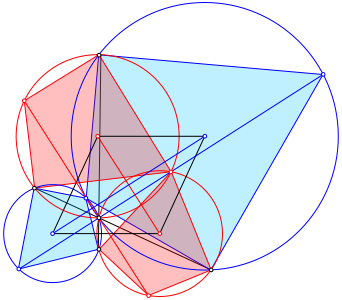
Abb. 13: Rhombus
Die Vierecke sind zueinander Šhnliche Drachenvierecke. Die spitzen und stumpfen Winkel entsprechen denen des Rhombus.
8.3 Rechteck
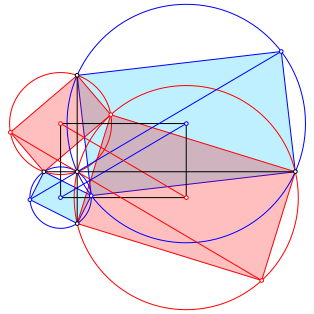
Abb. 14: Rechteck
Die Sehnenvierecke sind zueinander und zum Ausgangsrechteck Šhnliche Rechtecke.
Die FlŠchensumme der beiden roten Rechtecke ist gleich gro§ wie die FlŠchensumme der beiden blauen Rechtecke.
Die beiden schwarzen Strecken (vgl. Abb. 12) sind Winkelhalbierende der Winkel zwischen der roten beziehungsweise blauen Strecke (vgl. Abb. 4). Diese rote beziehungsweise blaue Strecke ist gleich lang.
8.4 Quadrat
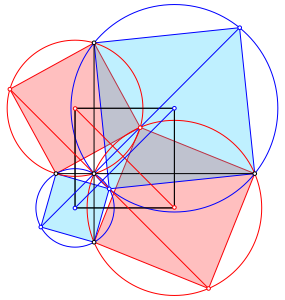
Abb. 15: Quadrat
Wir haben ausschlie§lich Quadrate.
Es gelten alle oben festgestellten Eigenschaften.