Hans Walser, [20070326a]

1 Im Dreieck: Spiralen zum Schwerpunkt

In einem Dreieck werden die drei Seiten zyklisch im gleichen Verhältnis unterteilt. Die drei Teilpunkte bilden ein neues Dreieck, mit dem ebenso verfahren wird. Und so weiter.

Die Figur zeigt ein Ausgangsdreieck und den ersten und den zweiten Schritt bei einem Teilverhältnis von .

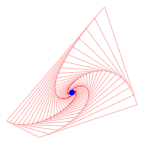
Schritte eins und zwei

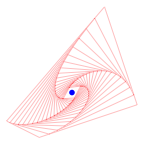
Im folgenden Bild sind die ersten 50 Schritte eingezeichnet. Zusätzlich ist blau der Schwerpunkt des Ausgangsdreieckes markiert.

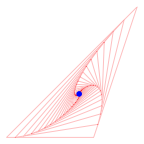
50 Schritte, Schwerpunkt

Wir vermuten: Die drei „Spiralen“ (in Wirklichkeit Polygone) streben zum Schwerpunkt. Wie lässt sich das beweisen?

1.1 Beweis

Für das reguläre Dreieck ist die Aussage aus Symmetriegründen klar. Der Übergang von einem Dreieck zum nächsten kann durch eine Drehstreckung mit Zentrum im Ursprung beschreiben werden. Die Spiralen sind daher logarithmische Spiralen.

Reguläres Dreieck

Wir können nun das reguläre Dreieck affin auf ein allgemeines Dreieck abbilden. Die Teilverhältnisse bleiben dabei erhalten. Da unsere Spiralen wie auch der Schwerpunkt mit Teilverhältnissen definiert sind, bleibt die Eigenschaft erhalten, dass die Spiralen in den Schwerpunkt einmünden. Allerdings sind die affin verzerrten logarithmischen Spiralen im allgemeinen keine logarithmische Spiralen mehr.

1.2 Gemeinsamer Schwerpunkt

Im affin verzerrten Fall sind die Dreiecke nicht mehr ähnlich. Hingegen haben alle Dreiecke denselben Schwerpunkt:

Es sei der Schwerpunkt im Dreieck .

Es ist also:

Die Ecken des nachfolgenden Dreieckes erhalten wir mit dem Faktor durch:

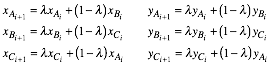
Für den Schwerpunkt ergibt sich:

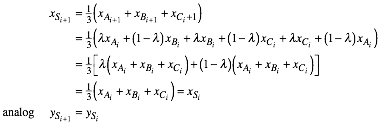
Der Schwerpunkt ist also invariant.

1.3 Verallgemeinerung

Ein n-Eck mit kann im allgemeinen nicht affin auf ein anderes n-Eck mit abgebildet werden. Unser Beweis ist in diesem Fall nicht anwendbar.

Hingegen ist die Überlegung mit dem gemeinsamen Schwerpunkt auf ein n-Eck mit verallgemeinerungsfähig.

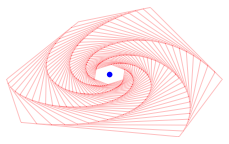
Die Sache mit den Spiralen scheint auch für zu stimmen.

Viereck

Mehr noch: die „kleinen“ Vierecke scheinen sich je einem Parallelogramm anzunähern. Wir sehen das, wenn wir in der Mitte ein Loch offen lassen.

Parallelogramm in der Mitte?

So überraschend ist das nicht. Wenn wir in einem beliebigen Ausgangsviereck die Seitenmitten verbinden, erhalten wir auf Anhieb ein Parallelogramm.

Ein Parallelogramm ist nun aber ein affin verzerrtes Quadrat. Damit könnten wir, wenn die Sache mit dem Parallelogramm wirklich stimmt, wohl mit der Überlegung der affinen Verzerrung eines Quadrates arbeiten.

Auch beim Sechseck ergibt sich in der Mitte ein annähernd affin-reguläres Sechseck.

Affin-reguläres Sechseck in der Mitte?