Hans Walser, [20090413a]
Spiralen gesucht
1 Archimedische Spirale gesucht
Gesucht
ist die archimedische Spirale mit Zentrum im Ursprung durch zwei gegebene
Punkte. Beispiel: 
und 
(in kartesischen
Koordinaten)
Bearbeitung
und 
seien die beiden
Punkte in Polarkoordinaten. Dann ist
die
Polargleichung der gesuchten archimedischen Spirale.
Beispiel:
und 
(in kartesischen
Koordinaten)
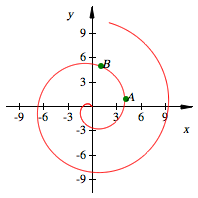
Archimedische
Spirale
Hier wird
allerdings vorausgesetzt, dass sich die beiden Punkte A und B auf demselben †berlagerungsblatt
befinden. Wenn sich B von A aus gesehen k Runden weiter befindet, muss
der Polarwinkel auf 
abgeŠndert
werden:
Fźr 
erhalten wir:
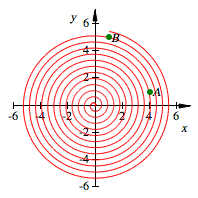
B ist zwei Runden weiter
Fźr 
ergibt sich:
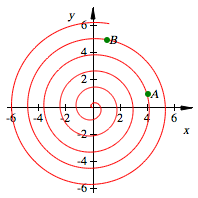
B liegt eine Runde zurźck
2 Logarithmische Spirale gesucht
Gesucht
ist die logarithmische Spirale mit Zentrum im Ursprung durch zwei gegebene
Punkte. Beispiel: 
und 
(in kartesischen
Koordinaten)
Bearbeitung
und 
seien die beiden
Punkte in Polarkoordinaten. Mit k bezeichnen wir,
wie viele BlŠtter sich B oberhalb oder unterhalb
von A befindet. Dann ist
die
Polargleichung der gesuchten logarithmischen Spirale.
Beispiel:
und 
(in kartesischen
Koordinaten), 
:
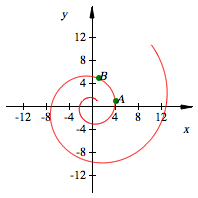
Logarithmische
Spirale
Fźr 
erhalten wir:
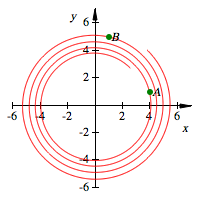
B ist zwei Runden weiter
Fźr 
ergibt sich:
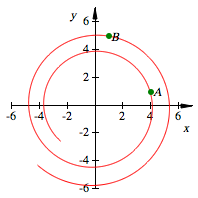
B liegt eine Runde zurźck