1 Ausgangslage

In ein Parallelogramm mit einem spitzen Winkel 60° und dem Seitenverhältnis im Goldenen Schnitt (Walser 2013) können zwei aus gleichseitigen Dreiecken zusammengesetzt Spiralen eingezeichnet werden (Abb. 1).

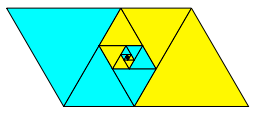
Abb. 1: Spiralen aus gleichseitigen Dreiecken

Die Abbildung 2 zeigt ein Beispiel mit rechtwinklig gleichschenkligen Dreiecken.

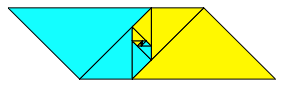
Abb. 2: Rechtwinklig gleichschenklige Dreiecke

Das Seitenverhältnis des Parallelogramms ist:

(1)

2 Problemstellung

In welche Parallelogramme lassen sich zwei aus gleichschenkligen Dreiecke zusammengesetzte Spiralen einfügen?

3 Witz der Sache

Abb. 3: Ähnliche Parallelogramme

Das Innere der Figur (weiß in Abb. 3) ist ähnlich zur Gesamtfigur.

4 Maße und Bezeichnungen

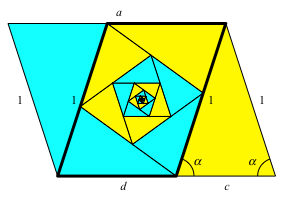
Abb. 4: Maße und Bezeichnungen

Die beiden gleichschenkligen Start-Dreiecke haben die Schenkellänge b = 1. Dies ist auch die kürzere Seite des Parallelogramms. Der Basiswinkel der gleichschenkligen Dreiecke ist a. Dies ist auch der spitze Winkel des Parallelogramms und zudem der Drehwinkel der Drehstreckung, welche die Gesamtfigur auf die Innenfigur abbildet. Der Streckfaktor ist d.

5 Etwas Rechnung

Es ist:

(2)

Die Ähnlichkeitsbedingung ist:

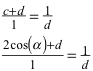(3)

Dies ergibt eine quadratische Gleichung für d:

(4)

Die positive Lösung dieser quadratischen Gleichung ist:

(5)

Für die Grundseite a des Parallelogramms ergibt sich aus (2) und (5):

(6)

Dies ist auch das Seitenverhältnis des Parallelogramms.

Auflösen von (6) nach a ergibt:

(7)

Die Bedingungen (6) beziehungsweise (7) beschreiben die Parallelogramme, in welche sich zwei Spiralen aus gleichschenkligen Dreiecken einzeichnen lassen.

6 Weitere Beispiele

Für a = 30° (Abb. 5) ergibt sich das Seitenverhältnis:

(8)

Abb. 5: a = 30°

Für a = 75° (Abb. 6) ergibt sich das Seitenverhältnis ~1.291769817.

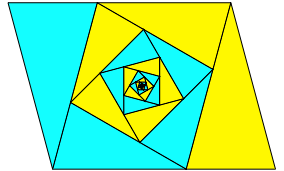
Abb. 6: a = 75°

Literatur

Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.