Hans Walser, [20210502]
Spiralen in Rechtecken
1 Worum geht es?
In Rechtecke werden eckige logarithmische Spiralen eingebaut. Dabei wird mit rechtwinkligen Dreiecken gearbeitet. Wir erhalten auch einen geometrischen Zugang zu pythagoreischen Dreiecken.
Viele Bildchen.
2 Beispiele
Die Rechtecke haben die Seiten u und v mit u > v. Quadrate sind also ausgeschlossen.
2.1 Das silberne Rechteck
Das
sogenannte silberne Rechteck hat das Seitenverhltnis ![]() .
Es kann mit vier rechtwinklig gleichschenkligen Dreiecken (Geo-Dreiecken)
ausgelegt werden (Abb. 1). Der Diagonalenschnittwinkel misst 45¡.
.
Es kann mit vier rechtwinklig gleichschenkligen Dreiecken (Geo-Dreiecken)
ausgelegt werden (Abb. 1). Der Diagonalenschnittwinkel misst 45¡.

Abb.1: Silbernes Rechteck
Das Loch in der Mitte ist ebenfalls ein silbernes Rechteck (Beweis allgemein mit Rechnung, siehe unten). Wir knnen also eine geeignet verkleinerte und verdrehte Kopie der Figur der Abbildung 1 einpassen (Abb. 2).
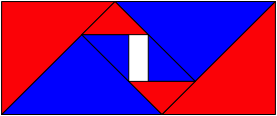
Abb. 2: Einpassen einer Kopie
Iteration des Prozesses fhrt zu vier Flchenspiralen (Abb. 3).
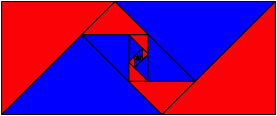
Abb. 3: Vier Flchenspiralen
Eine rote und eine blaue Flchenspirale bestehen aus den gleichen Dreiecken. Sie sind also flchengleich. Sie sind aber nicht kongruent. Bei der roten Flchenspirale ist eine Kathete des nachfolgenden Dreiecks an die Hypotenuse des vorangehenden Dreiecks angesetzt. Bei der blauen Flchenspirale ist es umgekehrt.
Die Abbildung 4 zeigt die Randlinien der vier Flchenspiralen. Diese Randlinien sind kongruent.
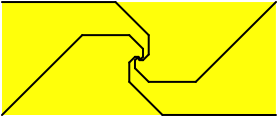
Abb. 4: Randlinien
Die Randlinien sind eckige logarithmische Linienspiralen. Ihre Ecken liegen auf logarithmischen Spiralen (Abb. 5).
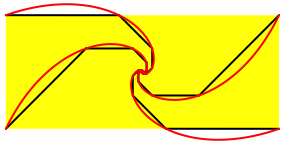
Abb. 5: Logarithmische Spiralen
Die roten Flchenspiralen haben im Zentrum — intuitiv gesprochen — einen spitzeren ãWinkelÒ als die blauen. Die Frage ist, wie ein solcher ãWinkelÒ definiert werden kann.
Die eckigen logarithmischen Spiralen der Abbildung 4 knnen um 90¡ gedreht werden. Die Gesamtfigur passt in ein regelm§iges Achteck (Abb. 6).
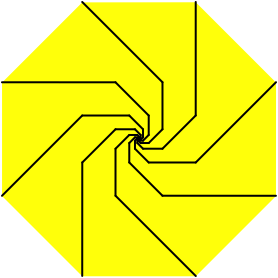
Abb. 6: Regelm§iges Achteck
Entsprechend knnen wir acht Flchenspiralen der roten Sorte (Abb. 3) in ein regelm§iges Achteck einpassen (Abb. 7).
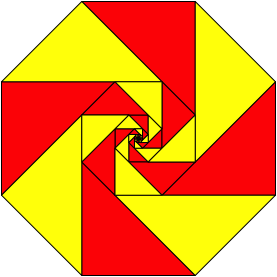
Abb. 7: Acht Flchenspiralen im Achteck
Es ist daher sinnvoll, den roten Flchenspiralen im Zentrum einen Winkel von 45¡ zuzuordnen. Den blauen Flchenspiralen (Abb. 3) knnen wir den Ergnzungswinkel 135¡ zuordnen. Diese Winkel entsprechen den Schnittwinkeln der Diagonalen des silbernen Rechteckes.
Der Winkel 135¡ der blauen Flchenspiralen ist kein Teiler des vollen Winkels 360¡. Wir knnen daher mit den blauen Flchenspiralen allein nicht den vollen Winkel ausfllen.
Hingegen knnen wir die zyklische Reihenfolge von zwei Flchenspiralen mit einem Zentrumswinkel 45¡ und zwei Flchenspiralen mit einem Zentrumswinkel 135¡ abndern. In der Abbildung 8 haben wir die Situation 45¡ + 135¡ +135¡ + 45¡. Der Umriss der Gesamtfigur ist ein Drachenviereck, das gleichzeitig in Sehnenviereck ist. Der spitze Winkel ist 45¡.
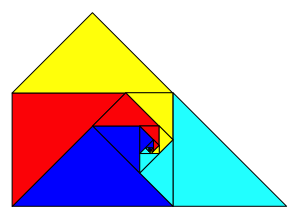
Abb. 8: Andere zyklische Reihenfolge
Die Figur lsst sich in ein regelm§iges Achteck einpassen (Abb. 9).
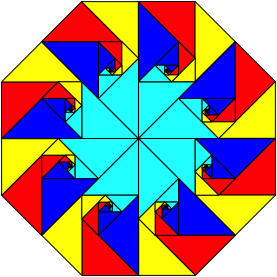
Abb. 9: Im Acheck
2.2 30¡-60¡-90¡-Dreiecke
Wir
arbeiten mit rechtwinkligen Dreiecken mit den Winkeln 30¡, 60¡ und 90¡. Das entstehende
Rechteck (Abb. 10) hat den Diagonalenschnittwinkel 60¡. Das Seitenverhltnis ist ![]() .
.
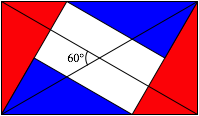
Abb. 10: Diagonalenschnittwinkel 60¡
Entsprechend haben die Flchenspiralen den Zentrumswinkel 60¡ und 120¡ (Abb. 11).
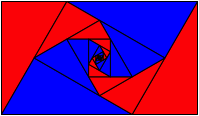
Abb. 11: Flchenspiralen mit Zentrumswinkeln 60¡ und 120¡
Wir knnen sechs Flchenspiralen mit Zentrumswinkel 60¡ in ein regelm§iges Sechseck einpassen (Abb. 12).
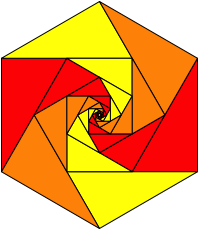
Abb. 12: Im Sechseck
Wir knnen aber auch drei Flchenspiralen mit einem Zentrumswinkel 120¡ in ein gleichseitiges Dreieck einpassen (Abb. 13).
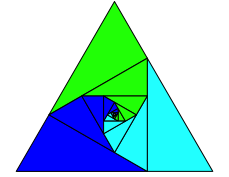
Abb. 13: Im Dreieck
Die Figur lsst sich trivialerweise in ein regelm§iges Sechseck einpassen (Abb. 14).
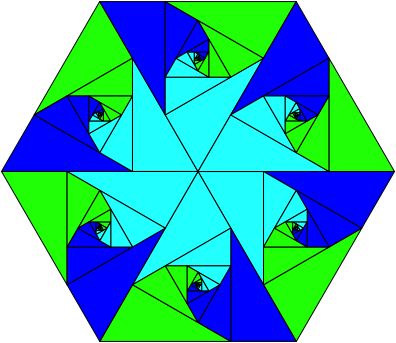
Abb. 14: Im Sechseck
Die Abbildung 15 zeigt eine andere zyklische Reihenfolge der Flchenspiralen der Abbildung 11. Die Zentrumswinkel sind 60¡ + 120¡ + 120¡ + 60¡.
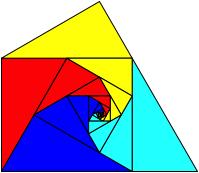
Abb. 15: Andere Reihenfolge
Wir erhalten ein Drachenviereck, das gleichzeitig ein Sehnenviereck ist. Der spitze Winkel ist 60¡. Sechs solche Figuren knnen wir zu einem regelm§igen Sechseck zusammenfgen (Abb. 16).
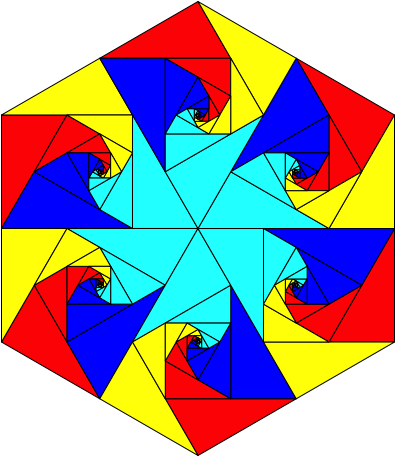
Abb. 16: Im Sechseck
Die Abbildung 17 zeigt eine Mischversion mit einer 120¡-Flchenspirale (blau) und vier 60¡-Flchenspiralen.
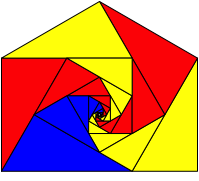
Abb. 17: Mischversion
Mit Figuren der Abbildung 17 kann ein Parkett ausgelegt werden (Abb. 18).

Abb. 18: Parkett
2.3 18¡-72¡-90¡-Dreiecke
Wir arbeiten mit rechtwinkligen Dreiecken mit den Winkeln 18¡, 72¡ und 90¡. Das entstehende Rechteck (Abb. 19) hat den Diagonalenschnittwinkel 72¡.

Abb.19: Diagonalenschnittwinkel 72¡
Entsprechend haben die Flchenspiralen den Zentrumswinkel 72¡ und 108¡ (Abb. 20).
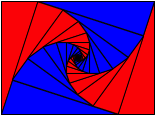
Abb. 20: Flchenspiralen mit Zentrumswinkeln 72¡ und 108¡
Wir knnen die zyklische Reihenfolge der Flchenspiralen verndern. Die Abbildung 21 zeigt die Version mit der Reihenfolge 72¡ + 108¡ + 108¡ + 72¡.
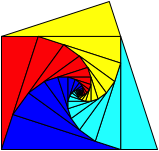
Abb. 21: Andere Reihenfolge
Wir erhalten ein Drachenviereck, das gleichzeitig ein Sehnenviereck ist. Der spitze Winkel ist 72¡. Wir knnen daher die Figur in ein regelm§iges Fnfeck einpassen (Abb. 22).
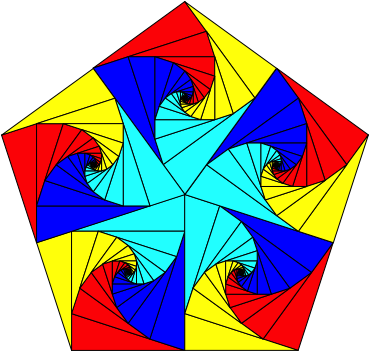
Abb. 22: Im Fnfeck
Mit regelm§igen Fnfecken lsst sich kein Parkett auslegen. Hingegen knnen wir mit den Drachenvierecken der Abbildung 21 ein Parkett auslegen (Abb. 23).
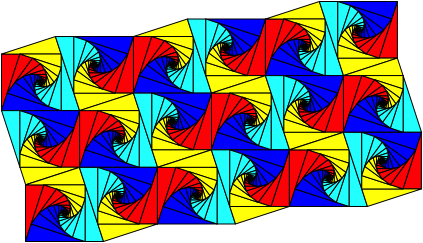
Abb. 23: Parkett
Weiter knnen wir natrlich auch fnf Flchenspiralen mit einem Zentrumswinkel 72¡ in ein regelm§iges Fnfeck einpassen (Abb. 24).
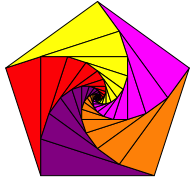
Abb. 24: Im Fnfeck
2.4 Im DIN-Rechteck
Das
DIN-Rechteck hat ein Seitenverhltnis ![]() .
Sein Diagonalenschnittwinkel ist
.
Sein Diagonalenschnittwinkel ist ![]() .
Da dieser Winkel kein Teiler von 360¡ ist, besteht auch keine Mglichkeit des
Einbettens der Flchenspiralen in ein regelm§iges Vieleck. Die Abbildung 25
zeigt die Startsituation. Der gr§ere der beiden spitzen Winkel der rechtwinkligen
Dreiecke ist gleich dem Diagonalenschnittwinkel. Das schrge Loch ist ebenfalls
ein DIN-Rechteck.
.
Da dieser Winkel kein Teiler von 360¡ ist, besteht auch keine Mglichkeit des
Einbettens der Flchenspiralen in ein regelm§iges Vieleck. Die Abbildung 25
zeigt die Startsituation. Der gr§ere der beiden spitzen Winkel der rechtwinkligen
Dreiecke ist gleich dem Diagonalenschnittwinkel. Das schrge Loch ist ebenfalls
ein DIN-Rechteck.

Abb. 25: Start im DIN-Rechteck
Wir erhalten schlie§lich vier Flchenspiralen, zwei mit dem Zentrumswinkel von etwa 70.5288¡ und zwei mit dem Zentrumswinkel von etwa 109.4712¡. Diese beiden Winkel sind die Diederwinkel (Winkel zwischen zwei Seitenflchen mit gemeinsamer Kante) des regelm§igen Tetraeders beziehungsweise des regelm§igen Oktaeders.

Abb. 26: Flchenspiralen im DIN-Rechteck
Da der Zentrumswinkel der Flchenspiralen kein Teiler von 360¡ ist, ergibt sich beim Zusammenfgen eine Lcke (Abb. 27).
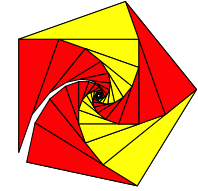
Abb. 27: Lcke
Wie blich knnen wir die zyklische Reihenfolge der Figur der Abbildung 26 verndern und erhalten ein Drachenviereck, das auch ein Sehnenviereck ist (Abb. 28).
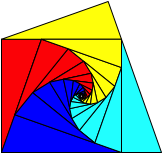
Abb. 28: Vernderte Reihenfolge
3 Allgemein
Das Spielchen mit den vier Flchenspiralen kann in einem beliebigen Rechteck (ausgenommen in einem Quadrat) gemacht werden.
3.1 Das rechtwinklige Dreieck
Das fr die Flchenspiralen bentigte rechtwinklige Dreieck kann auf zwei Arten konstruiert werden.
Die erste Methode geht so: Wir schneiden gem§ Abbildung 29 die Mittelsenkrechte einer Rechteckdiagonalen mit einer Langseite des Rechteckes und erhalten zusammen mit einer Schmalseite des Rechteckes das gesuchte rechtwinklige Dreieck.
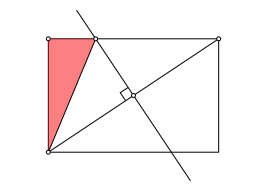
Abb. 29: Konstruktion des Startdreieckes
Begrndung: In der Startsituation mit vier kongruenten rechtwinkligen Dreiecken bilden die vier Hypotenusen einen Rhombus (Abb. 30). Unsere Diagonalen-Konstruktion fhrt zu diesem Rhombus.
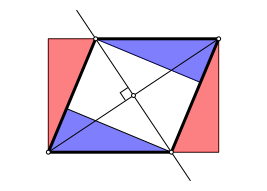
Abb. 30: Rhombus
Das in der Abbildung 31 gelb markierte Viereck hat zwei gegenberliegende rechte Winkel und ist daher in Sehnenviereck. Der Umkreis dieses Sehnenvierecks verluft durch zwei mit einer Schmalseite verbundene Rechteck-Ecken und den Mittelpunkt des Rechteckes. Damit erhalten wir die zweite Methode zur Konstruktion des fr die Flchenspirale bentigten rechtwinkligen Dreieck: wir zeichnen den Kreis durch zwei mit einer Schmalseite verbundene Ecken und den Mittelpunkt des Rechteckes und schneiden diesen Kreis mit einer Langseite.
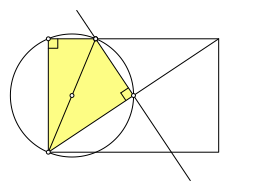
Abb. 31: Sehnenviereck
Wir interpretieren nun diesen Kreis als Ortsbogen ber der Schmalseite (Abb. 32):
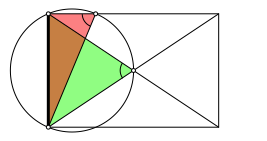
Abb. 32: Ortsbogen
Damit wird klar, dass der gr§ere der beiden spitzen Winkel des rechtwinkligen Dreiecks gleich dem Diagonalen-Schnittwinkels des Rechteckes ist.
3.2 Etwas Rechnung
Wir arbeiten mit den Bezeichnungen der Abbildung 33.
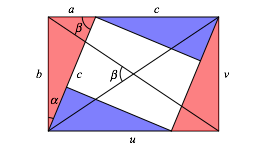
Abb. 33: Bezeichnungen
Es ist:
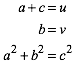 (1)
(1)
Zu gegebenem u, v ist (1) ein Gleichungssystem fr a, b, c. Es hat die Lsung:
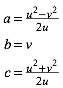 (2)
(2)
Das
Lochrechteck hat die Langseite b = v und die Schmalseite ![]() .
Damit erhalten wir das Seitenverhltnis:
.
Damit erhalten wir das Seitenverhltnis:
![]() (3)
(3)
Das Lochrechteck ist also hnlich zum Startrechteck.
Die
Transformation vom Startrechteck auf das Lochrechteck ist eine Drehstreckung
mit dem Zentrum im Mittelpunkt des Startrechteckes. Der Drehwinkel ist der Winkel ![]() ,
der kleinere der beiden spitzen Winkel des rechtwinkligen Dreiecks. Das ist der
Ergnzungswinkel des Diagonalen-Schnittwinkels
,
der kleinere der beiden spitzen Winkel des rechtwinkligen Dreiecks. Das ist der
Ergnzungswinkel des Diagonalen-Schnittwinkels ![]() auf den rechten Winkel. Es ist:
auf den rechten Winkel. Es ist:
![]() (4)
(4)
Fr den Streckfaktor f erhalten wir:
![]() (5)
(5)
4 Pythagoreische Spiralen
4.1 Beispiel
Fr u = 2 und v = 1 erhalten wir nach (2):
![]() (6)
(6)
Das ist das einfachste pythagoreische Dreieck (Abb. 34).
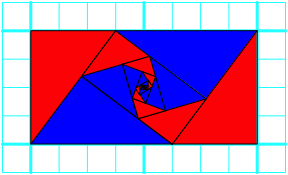
Abb. 34: Pythagoreische Dreiecke und Spiralen
Es ist ![]() und
und ![]() .
.
4.2 Allgemein
Primitive (teilerfremde) pythagoreische Zahlentripel knnen wie folgt parametrisiert werden: wir whlen zwei teilerfremde natrliche Zahlen u, v ungleicher Paritt (nicht beide gerade oder beide ungerade) mit u > v. Dann ist
![]() (7)
(7)
ein pythagoreisches Zahlentripel. Vergleich mit (2) zeigt, dass unser rechtwinkliges Dreieck (bis auf den Skalierungsfaktor 2u) das zugehrige pythagoreische Dreieck ist. Wir haben also (Abschnitt 3.1) zwei geometrische Methoden, aus u und v das zugehrige pythagoreische Dreieck zu konstruieren.
Websites
Hans
Walser: Rechtecksunterteilung
http://www.walser-h-m.ch/hans/Miniaturen/R/Rechtecksunterteilung3/Rechtecksunterteilung3.htm