Hans Walser, [20200712]

Spiralen im regelmŠ§igen Vieleck

Anregung: M. E., B.

1     Worum es geht

Im Kontext von regelmŠ§igen n-Ecken werden Spiralen gegebener LŠnge gesucht.

Wir treffen dabei auf pythagoreische Dreiecke.

2     Im Dreieck

In einem gleichseitigen Dreieck setzen wir die Folge der Kantenmittendreiecke ein (Abb. 1).

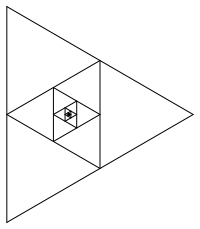
Abb. 1: Kantenmittendreiecke

Wir zeichnen eine Kantenmittenspirale ein (Abb. 2).

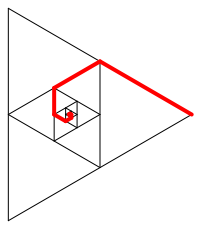
Abb. 2: Kantenmittenspirale

Bezogen auf die SeitenlŠnge 1 des Dreieckes hat die Kantenmittenspirale die LŠnge s:

 

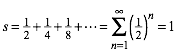                                                                               (1)

 

 

 

Die Kantenmittenspirale ist gleich gro§ wie die SeitenlŠnge des Dreiecks.

 

3     Im Quadrat

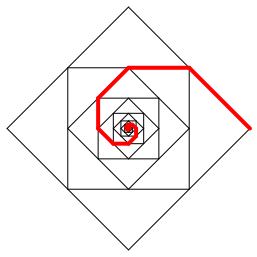
Abb. 3: Im Quadrat

Das analoge Spielchen im Quadrat (Abb. 3) fźhrt zu einer Kantenmittenspirale der LŠnge s:

 

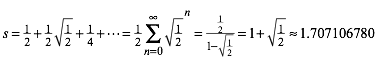           (2)

 

 

 

 

4     Problemstellung

Wie muss die Kantenmittenfigur modifiziert werden, um eine vorgegebene SpiralenlŠnge, insbesondere eine ganzzahlige SpiralenlŠnge, zu erhalten?

5     Andere Unterteilung der Kanten

Wir unterteilen die Kanten des n-Eckes in einem anderen VerhŠltnis.

Beispiel: Wir unterteilen die Quadratseite im VerhŠltnis  (Abb. 4).

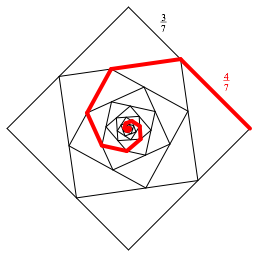
Abb. 4: Unterteilung im VerhŠltnis 4:3

In dieser Situation erhalten wir die SpiralenlŠnge 2. Dies kšnnen wir einsehen wie folgt.

Abb. 5: Beweisfigur

Das gelbe rechtwinklige Dreieck in der Beweisfigur (Abb. 5) hat die Katheten  und  und daher die Hypotenuse . Dies ist auch der LŠngenreduktionsfaktor  von einem Quadrat zum nachfolgenden Quadrat.

Die Startstrecke  der Spirale ist . Fźr die nachfolgenden Strecken ergibt sich jedes Mal eine Reduktion mit dem Faktor q:

 

                          (3)

 

 

 

 

Damit erhalten wir fźr die gesamte SpiralenlŠnge s:

 

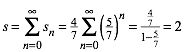                                                                            (4)

 

 

 

 

Bemerkung: Das gelbe Dreieck in der Abbildung 5 ist ein pythagoreisches Dreieck.

6     Allgemein

Zu gegebener SpiralenlŠnge s und gegebener Eckenzahl n suchen wir ein passendes TeilverhŠltnis . (Im Beispiel der Abbildung 5 ist s = 2, n = 4 und ).

In der Arbeitsfigur (Abb. 6) wurde n = 5 gewŠhlt.

Wir berechnen die Seite q des gelben Dreiecks. Es hat die beiden źbrigen Seiten  und  und den der gesuchten Seite q gegenźberliegenden Winkel .

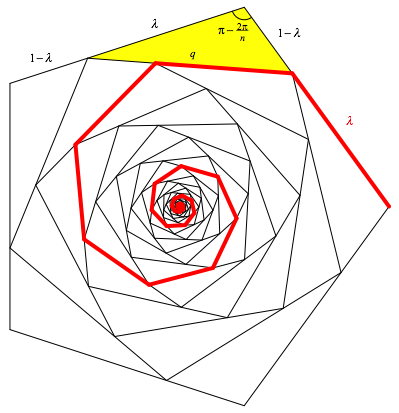
Abb. 6: Arbeitsfigur

Der Kosinus-Satz liefert:

 

                                                       (5)

 

 

 

Dies kann umgeformt werden zu:

 

                                                   (6)

 

 

 

Da q der LŠngenreduktionsfaktor von einem n-Eck zum nachfolgenden ist, ergibt sich fźr die SpiralenlŠnge s:

 

                                                                                                                           (7)

 

 

 

Die Beziehung (7) kann mit Einsetzen von (6) umgeformt werden zu:

 

                                   (8)

 

 

 

Die quadratische Gleichung (8) hat die triviale erste Lšsung , welche fźr uns nicht relevant ist. Die zweite Lšsung ist unser gesuchtes TeilverhŠltnis:

 

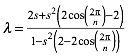                                                                                               (9)

 

 

 

 

7     Ganzzahlige SpiralenlŠngen

In den Abbildungen 2 und 4 hatten wir ganzzahlige SpiralenlŠngen. Wir kšnnen nun umgekehrt nach TeilverhŠltnissen  fragen, welche zu ganzzahligen SpiralenlŠngen fźhren.

Rationale TeilverhŠltnisse ergeben sich offenbar (unbewiesene Vermutung) nur fźr die Eckenzahlen n = 3, 4 und 6. Es zeigt sich, dass wir dabei auf pythagoreische Dreiecke sto§en.

7.1    Im Quadrat    

Die Tabelle 1 zeigt fźr n = 4 und die natźrlichen Zahlen fźr s die zugehšrigen TeilverhŠltnisse. Ebenso ist die ErgŠnzung der TeilverhŠltnisse auf 1 angegeben. Die ZŠhler b beziehungsweise a (Reihenfolge beachten) sind die Katheten eines pythagoreischen Dreiecks mit der Hypotenuse c. Es handelt sich dabei um die ăfast gleichschenkligenŇ pythagoreischen Dreiecke. Die Hypotenuse c ist jeweils um 1 grš§er als die Kathete b.

 

n

s

b

a

c

4

1

0

1

0

1

1

4

2

4/7

3/7

4

3

5

4

3

12/17

5/17

12

5

13

4

4

24/31

7/31

24

7

25

4

5

40/49

9/49

40

9

41

4

6

60/71

11/71

60

11

61

4

7

84/97

13/97

84

13

85

4

8

112/127

15/127

112

15

113

4

9

144/161

17/161

144

17

145

4

10

180/199

19/199

180

19

181

4

11

220/241

21/241

220

21

221

4

12

264/287

23/287

264

23

265

4

13

312/337

25/337

312

25

313

4

14

364/391

27/391

364

27

365

4

15

420/449

29/449

420

29

421

4

16

480/511

31/511

480

31

481

4

17

544/577

33/577

544

33

545

4

18

612/647

35/647

612

35

613

4

19

684/721

37/721

684

37

685

4

20

760/799

39/799

760

39

761

Tab. 1: Im Quadrat

7.2    Im gleichseitigen Dreieck

Die Tabelle 2 zeigt fźr n = 3 und die natźrlichen Zahlen fźr s die zugehšrigen TeilverhŠltnisse. Ebenso ist die ErgŠnzung der TeilverhŠltnisse auf 1 angegeben. Die ZŠhler b beziehungsweise a (Reihenfolge beachten) sind die Schenkel des 60ˇ-Winkels eines pythagoreischen 60ˇ-Dreieckes. Die Seite c ist jeweils um s – 1 grš§er als die Seite b.

 

n

s

b

a

c

3

1

1/2

1/2

1

1

1

3

2

8/11

3/11

8

3

7

3

3

21/26

5/26

21

5

19

3

4

40/47

7/47

40

7

37

3

5

65/74

9/74

65

9

61

3

6

96/107

11/107

96

11

91

3

7

133/146

13/146

133

13

127

3

8

176/191

15/191

176

15

169

3

9

225/242

17/242

225

17

217

3

10

280/299

19/299

280

19

271

3

11

341/362

21/362

341

21

331

3

12

408/431

23/431

408

23

397

3

13

481/506

25/506

481

25

469

3

14

560/587

27/587

560

27

547

3

15

645/674

29/674

645

29

631

3

16

736/767

31/767

736

31

721

3

17

833/866

33/866

833

33

817

3

18

936/971

35/971

936

35

919

3

19

1045/1082

37/1082

1045

37

1027

3

20

1160/1199

39/1199

1160

39

1141

Tab. 2: Im gleichseitigen Dreieck

Die Abbildung 7 illustriert das zweite Beispiel mit den Seiten 3, 8 und 7.

Abb. 7: Pythagoreisches 60ˇ-Dreieck

7.3    Im regelmŠ§igen Sechseck

Die Tabelle 3 zeigt fźr n = 6 und die natźrlichen Zahlen fźr s die zugehšrigen TeilverhŠltnisse. Ebenso ist die ErgŠnzung der TeilverhŠltnisse auf 1 angegeben. Die ZŠhler b beziehungsweise a (Reihenfolge beachten) sind die Schenkel des 120ˇ-Winkels eines pythagoreischen 120ˇ-Dreieckes.

 

n

s

b

a

c

6

2

0

1

0

1

1

6

3

3/8

5/8

3

5

7

6

4

8/15

7/15

8

7

13

6

5

5/8

3/8

5

3

7

6

6

24/35

11/35

24

11

31

6

7

35/48

13/48

35

13

43

6

8

16/21

5/21

16

5

19

6

9

63/80

17/80

63

17

73

6

10

80/99

19/99

80

19

91

6

11

33/40

7/40

33

7

37

6

12

120/143

23/143

120

23

133

6

13

143/168

25/168

143

25

157

6

14

56/65

9/65

56

9

61

6

15

195/224

29/224

195

29

211

6

16

224/255

31/255

224

31

241

6

17

85/96

11/96

85

11

91

6

18

288/323

35/323

288

35

307

6

19

323/360

37/360

323

37

343

6

20

120/133

13/133

120

13

127

Tab. 3: Im regelmŠ§igen Sechseck

Die Abbildung 8 illustriert das zweite Beispiel mit den Seiten 5, 3 und 7.

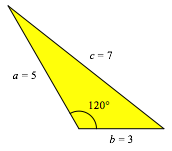
Abb. 8: Pythagoreisches 120ˇ-Dreieck

7.4    Im regelmŠ§igen Fźnfeck

Die Tabelle 4 zeigt fźr n = 5 und die natźrlichen Zahlen fźr s die zugehšrigen TeilverhŠltnisse. Sie sind vermutlich nicht rational.

 

n

s

5

1

–1.618033981

5

2

0.3374359374

5

3

0.5628489493

5

4

0.6684264726

5

5

0.7317368721

5

6

0.7743625681

5

7

0.8051451706

5

8

0.8284652236

5

9

0.8467629765

5

10

0.8615126043

5

11

0.8736598069

5

12

0.8838402059

5

13

0.8924972803

5

14

0.8999501004

5

15

0.9064342135

5

16

0.9121273596

5

17

0.9171662166

5

18

0.9216576328

5

19

0.9256863564

5

20

0.9293204768

Tab. 4: Im regelmŠ§igen Fźnfeck

Websites

Hans Walser: Kantenmittenspirale

www.walser-h-m.ch/hans/Miniaturen/K/Kantenmittenspirale/Kantenmittenspirale.htm

 

 

Literatur

Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.