Hans Walser, [20181007]

Spiralenabstand

1 Worum geht es?

Eine Rechenübung

2 Konstruktion

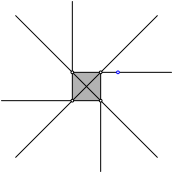
Abb. 1: Ausgangsfigur

Auf einer der verlängerten Seiten des Einheitsquadrates wählen wir einen beliebigen Startpunkt (Abb. 1).

Nun zeichnen wir Achtelbögen gemäß Abbildung 2. So entsteht der Beginn einer Spirale.

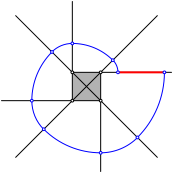
Abb. 2: Spiralenanfang

Wenn wir die Konstruktion weiterführen, entsteht eine Spirale.

Wie groß ist die rote Strecke, also der Spiralenabstand?

3 Bearbeitung

In der Abbildung 3 sind die Bogenradien eingezeichnet.

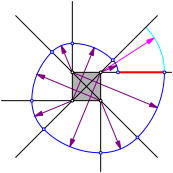
Abb. 3: Bogenradien

Wir nummerieren die Radien von innen nach außen.

Der innerste Radius ist frei wählbar (entsprechend der freien Wählbarkeit des Startpunktes). Weiter gilt:

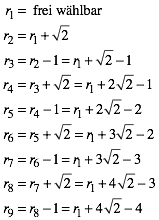(1)

Die Länge der roten Strecke ist:

(2)

Dieser Länge ist unabhängig vom gewählten Startpunkt. Das heißt, das sich eine Art archimedischer Spirale entwickelt.