Hans Walser, [20200807]
SpiralenlŠnge
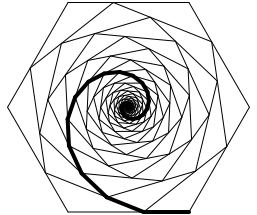
Abb. 1: Spirale im Sechseck
Die Dreiecke haben alle dieselbe Form. Bei welchem SeitenverhŠltnis dieser Dreiecke ist die Spirale halb so lang wie der Umfang des Sechseckes?
Bearbeitung
Bezeichnungen gemŠ§ Abbildung 2.
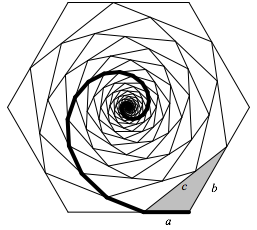
Abb. 2: Bezeichnungen
Die
StreckenlŠngen der Spirale bilden eine geometrische Folge mit dem Startglied a und dem Quotienten 
. Die SpiralenlŠnge s ist also:
(1)
Der halbe Umfang des Sechseckes ist 3(a + b). Somit haben wir die Bedingung:
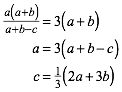(2)
Die
Dreiecke haben einen stumpfen Winkel 
. Der Kosinus-Satz liefert:
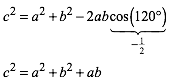(3)
Aus (2) und (3) ergibt sich:
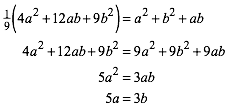(4)
Es ist also a:b = 3:5. Mit a = 3 und b = 5 ergibt sich c = 7. Somit ist das gesuchte SeitenverhŠltnis a:b:c = 3:5:7.
Es geht alles mit rationalen Dingen zu.
Websites
Hans Walser: Pythagoreische Spiralen
www.walser-h-m.ch/hans/Miniaturen/P/Pythagoreische_Spiralen2/Pythagoreische_Spiralen2.htm
Hans Walser: Spiralen im regelmŠ§igen Vieleck
www.walser-h-m.ch/hans/Miniaturen/S/Spiralen_reg_Vieleck/Spiralen_reg_Vieleck.htm
Hans Walser: Pythagoreische Spiralen
www.walser-h-m.ch/hans/Miniaturen/P/Pythagoreische_Spiralen/Pythagoreische_Spiralen.htm
Hans Walser: Pythagoreische 60ˇ- und 120ˇ-Dreiecke
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth-60-Dreiecke/Pyth-60-Dreiecke.htm