Hans Walser, [20120521]

StammbrŸche

1        Problemstellung

In der Antike, so zum Beispiel im alten €gypten, gehšrte es zum guten Ton, BrŸche in eine Summe von StammbrŸchen zu zerlegen, also in BrŸche mit dem ZŠhler 1. Diese Zerlegung ist allerdings nicht immer eindeutig, wie folgende Beispiele zeigen:

2        Der gierige Algorithmus

2.1      SÕhŠt solangÕs hŠt

Wir gehen nun so vor, dass wir zu einem gegebenen Bruch den grš§ten Stammbruch nehmen, der noch im gegebenen Bruch enthalten ist. Diesen grš§ten Stammbruch finden wir, indem wir den Kehrwert des gegebenen Bruches auf die nŠchste ganze Zahl aufrunden, und davon wieder den Kehrwert nehmen.

Beispiel:

Somit ist  der grš§te Stammbruch, der in  enthalten ist.

Vom Rest nehmen wir wieder den grš§ten noch darin enthaltenen Stammbruch und so weiter und so fort. Dabei hoffen wir, dass es einmal ãaufgehtÒ im Sinne, dass der Rest ein Stammbruch wird.

In unserem Beispiel:

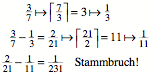
Somit haben wir eine Stammbruchzerlegung:

Das Verfahren wurde von Fibonacci in seinem Liber abaci beschrieben.

2.2      Formal

Es sei  der zu zerlegende Bruch. Dann arbeiten wir mit der folgenden Rekursion.

Start:

Rekursionsformel:

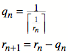
Abbruchkriterium: Wir hšren auf, sobald , also .

Wir erhalten die Stammbruchzerlegung:

Dass das Verfahren immer abbricht, wurde von James Joseph Sylvester 1880 bewiesen.

2.3      CAS-Programm

Ein Programm (MuPAD) kann so aussehen:

Stammbrueche:=proc(a,b)

begin

r[1]:=a/b:

rest:=a/b:

q[1]:=1/ceil(b/a):

n:=0:

while rest > 0 do

 n:=n+1:

 q[n]:=1/ceil(1/r[n]):

 r[n+1]:=r[n]-q[n]:

 rest:=r[n+1]:

end_while:

if n=1 then

 print(Unquoted,"".a."/".b." = ".q[1]);

else

 print(NoNL,"".a."/".b." = ".q[1]);

for k from 2 to n-1 do

 print(NoNL,"+".q[k]);

end_for:

print(Unquoted,"+".q[n]);

end_if:

end_proc:

 

FŸr unser Beispiel ergibt sich:

Stammbrueche(3,7);

 

3/7 = 1/3+1/11+1/231

Das Verfahren ist nicht optimal. Ein berŸhmtes Gegenbeispiel ist:

Der Algorithmus liefert eine Summe von vier StammbrŸchen:

Stammbrueche(59, 120);

 

59/120 = 1/3+1/7+1/65+1/10920

2.4      Liste

 

Zerlegung in StammbrŸche

________________________

 

geordnet nach Nennern

 

Nenner = 1

1/1 = 1

 

Nenner = 2

1/2 = 1/2

2/2 = 1

 

Nenner = 3

1/3 = 1/3

2/3 = 1/2+1/6

3/3 = 1

 

Nenner = 4

1/4 = 1/4

2/4 = 1/2

3/4 = 1/2+1/4

4/4 = 1

 

Nenner = 5

1/5 = 1/5

2/5 = 1/3+1/15

3/5 = 1/2+1/10

4/5 = 1/2+1/4+1/20

5/5 = 1

 

Nenner = 6

1/6 = 1/6

2/6 = 1/3

3/6 = 1/2

4/6 = 1/2+1/6

5/6 = 1/2+1/3

6/6 = 1

 

Nenner = 7

1/7 = 1/7

2/7 = 1/4+1/28

3/7 = 1/3+1/11+1/231

4/7 = 1/2+1/14

5/7 = 1/2+1/5+1/70

6/7 = 1/2+1/3+1/42

7/7 = 1

 

Nenner = 8

1/8 = 1/8

2/8 = 1/4

3/8 = 1/3+1/24

4/8 = 1/2

5/8 = 1/2+1/8

6/8 = 1/2+1/4

7/8 = 1/2+1/3+1/24

8/8 = 1

 

Nenner = 9

1/9 = 1/9

2/9 = 1/5+1/45

3/9 = 1/3

4/9 = 1/3+1/9

5/9 = 1/2+1/18

6/9 = 1/2+1/6

7/9 = 1/2+1/4+1/36

8/9 = 1/2+1/3+1/18

9/9 = 1

 

Nenner = 10

1/10 = 1/10

2/10 = 1/5

3/10 = 1/4+1/20

4/10 = 1/3+1/15

5/10 = 1/2

6/10 = 1/2+1/10

7/10 = 1/2+1/5

8/10 = 1/2+1/4+1/20

9/10 = 1/2+1/3+1/15

10/10 = 1

 

Nenner = 11

1/11 = 1/11

2/11 = 1/6+1/66

3/11 = 1/4+1/44

4/11 = 1/3+1/33

5/11 = 1/3+1/9+1/99

6/11 = 1/2+1/22

7/11 = 1/2+1/8+1/88

8/11 = 1/2+1/5+1/37+1/4070

9/11 = 1/2+1/4+1/15+1/660

10/11 = 1/2+1/3+1/14+1/231

11/11 = 1

 

Nenner = 12

1/12 = 1/12

2/12 = 1/6

3/12 = 1/4

4/12 = 1/3

5/12 = 1/3+1/12

6/12 = 1/2

7/12 = 1/2+1/12

8/12 = 1/2+1/6

9/12 = 1/2+1/4

10/12 = 1/2+1/3

11/12 = 1/2+1/3+1/12

12/12 = 1

 

Nenner = 13

1/13 = 1/13

2/13 = 1/7+1/91

3/13 = 1/5+1/33+1/2145

4/13 = 1/4+1/18+1/468

5/13 = 1/3+1/20+1/780

6/13 = 1/3+1/8+1/312

7/13 = 1/2+1/26

8/13 = 1/2+1/9+1/234

9/13 = 1/2+1/6+1/39

10/13 = 1/2+1/4+1/52

11/13 = 1/2+1/3+1/78

12/13 = 1/2+1/3+1/12+1/156

13/13 = 1

 

Nenner = 14

1/14 = 1/14

2/14 = 1/7

3/14 = 1/5+1/70

4/14 = 1/4+1/28

5/14 = 1/3+1/42

6/14 = 1/3+1/11+1/231

7/14 = 1/2

8/14 = 1/2+1/14

9/14 = 1/2+1/7

10/14 = 1/2+1/5+1/70

11/14 = 1/2+1/4+1/28

12/14 = 1/2+1/3+1/42

13/14 = 1/2+1/3+1/11+1/231

14/14 = 1

 

Nenner = 15

1/15 = 1/15

2/15 = 1/8+1/120

3/15 = 1/5

4/15 = 1/4+1/60

5/15 = 1/3

6/15 = 1/3+1/15

7/15 = 1/3+1/8+1/120

8/15 = 1/2+1/30

9/15 = 1/2+1/10

10/15 = 1/2+1/6

11/15 = 1/2+1/5+1/30

12/15 = 1/2+1/4+1/20

13/15 = 1/2+1/3+1/30

14/15 = 1/2+1/3+1/10

15/15 = 1

 

Nenner = 16

1/16 = 1/16

2/16 = 1/8

3/16 = 1/6+1/48

4/16 = 1/4

5/16 = 1/4+1/16

6/16 = 1/3+1/24

7/16 = 1/3+1/10+1/240

8/16 = 1/2

9/16 = 1/2+1/16

10/16 = 1/2+1/8

11/16 = 1/2+1/6+1/48

12/16 = 1/2+1/4

13/16 = 1/2+1/4+1/16

14/16 = 1/2+1/3+1/24

15/16 = 1/2+1/3+1/10+1/240

16/16 = 1

 

Nenner = 17

1/17 = 1/17

2/17 = 1/9+1/153

3/17 = 1/6+1/102

4/17 = 1/5+1/29+1/1233+1/3039345

5/17 = 1/4+1/23+1/1564

6/17 = 1/3+1/51

7/17 = 1/3+1/13+1/663

8/17 = 1/3+1/8+1/82+1/16728

9/17 = 1/2+1/34

10/17 = 1/2+1/12+1/204

11/17 = 1/2+1/7+1/238

12/17 = 1/2+1/5+1/170

13/17 = 1/2+1/4+1/68

14/17 = 1/2+1/4+1/14+1/476

15/17 = 1/2+1/3+1/21+1/714

16/17 = 1/2+1/3+1/10+1/128+1/32640

17/17 = 1

 

Nenner = 18

1/18 = 1/18

2/18 = 1/9

3/18 = 1/6

4/18 = 1/5+1/45

5/18 = 1/4+1/36

6/18 = 1/3

7/18 = 1/3+1/18

8/18 = 1/3+1/9

9/18 = 1/2

10/18 = 1/2+1/18

11/18 = 1/2+1/9

12/18 = 1/2+1/6

13/18 = 1/2+1/5+1/45

14/18 = 1/2+1/4+1/36

15/18 = 1/2+1/3

16/18 = 1/2+1/3+1/18

17/18 = 1/2+1/3+1/9

18/18 = 1

 

Nenner = 19

1/19 = 1/19

2/19 = 1/10+1/190

3/19 = 1/7+1/67+1/8911

4/19 = 1/5+1/95

5/19 = 1/4+1/76

6/19 = 1/4+1/16+1/304

7/19 = 1/3+1/29+1/1653

8/19 = 1/3+1/12+1/228

9/19 = 1/3+1/8+1/66+1/5016

10/19 = 1/2+1/38

11/19 = 1/2+1/13+1/494

12/19 = 1/2+1/8+1/152

13/19 = 1/2+1/6+1/57

14/19 = 1/2+1/5+1/28+1/887+1/2359420

15/19 = 1/2+1/4+1/26+1/988

16/19 = 1/2+1/3+1/114

17/19 = 1/2+1/3+1/17+1/388+1/375972

18/19 = 1/2+1/3+1/9+1/342

19/19 = 1

 

Nenner = 20

1/20 = 1/20

2/20 = 1/10

3/20 = 1/7+1/140

4/20 = 1/5

5/20 = 1/4

6/20 = 1/4+1/20

7/20 = 1/3+1/60

8/20 = 1/3+1/15

9/20 = 1/3+1/9+1/180

10/20 = 1/2

11/20 = 1/2+1/20

12/20 = 1/2+1/10

13/20 = 1/2+1/7+1/140

14/20 = 1/2+1/5

15/20 = 1/2+1/4

16/20 = 1/2+1/4+1/20

17/20 = 1/2+1/3+1/60

18/20 = 1/2+1/3+1/15

19/20 = 1/2+1/3+1/9+1/180

20/20 = 1

2.5      Anzahl der StammbrŸche

2.5.1     Bei gegebenen Nenner

Wir sehen, dass wir bei unserem Algorithmus mit relativ wenigen StammbrŸchen auskommen. Innerhalb eines gegebenen Nenners variiert die Anzahl der benštigten StammbrŸche bei verschiedenen ZŠhlern.

FŸr den Nenner 11 beispielsweise variiert die Anzahl der StammbrŸche zwischen 1 und 4. Dies wird im folgenden Diagramm dargestellt:

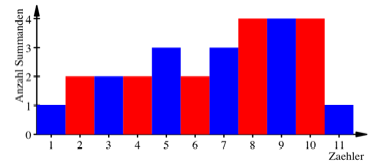
Anzahl der StammbrŸche beim Nenner 11

2.5.2     Maximale Anzahl

Im folgenden Diagramm wird zu gegebenem Nenner die maximale Anzahl der benštigten StammbrŸche dargestellt. Die Nenner laufen von 1 bis 20.

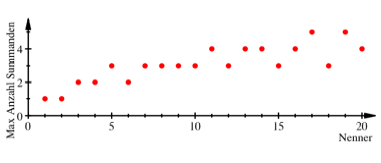
Maximale Anzahl der StammbrŸche

Im folgenden Diagramm wird die Situation fŸr Nenner von 1 bis 200 dargestellt. Die untere grŸne Kurve ist der Graf der Funktion , die obere der Graf der Funktion . 

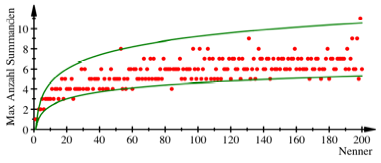
Nenner von 1 bis 200

Im Folgenden das Diagramm fŸr Nenner von 1 bis 1000.

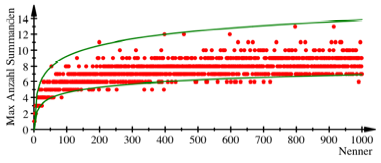
Nenner von 1 bis 1000

2.6      BrŸche grš§er als eins

Der Algorithmus funktioniert auch bei BrŸchen grš§er als eins und liefert ein eigenartiges Resultat, wie die Beispielfolge zeigt:

 

3/7 =         1/3+1/11+1/231

10/7 =       1+1/3+1/11+1/231

17/7 =     1+1+1/3+1/11+1/231

24/7 =   1+1+1+1/3+1/11+1/231

31/7 = 1+1+1+1+1/3+1/11+1/231

 

Der ganzzahlige Anteil wird in Einsen aufgedršselt.

2.7      Das Basler Problem

Nach Euler ist:

Das ist die Lšsung des so genannten Basler Problems.

Wir kšnnen nun versuchen, unseren Algorithmus auf den ãBruchÒ anzuwenden. NatŸrlich muss das schief gehen, da der ãBruchÒ irrational ist und die Stellenanzahl des Computers beschrŠnkt. Wir erhalten:

Erster Versuch:

 

Stammbrueche(PI^2, 6);

 

Error: Division by zero [_power];

during evaluation of 'ceil'

 

Zweiter Versuch: Wir ersetzen  durch eine Dezimalzahl mit 20 Stellen.

 

Stammbrueche(float(PI^2), 6);

 

9.8696044010893586188/6 = 1+1/2+1/7+1/482+1/447389+1/322140653777
+1/130370586212598241166765
+1/54572818080363359463254991838265141002061742080

 

3        Alternierende Summen

3.1      ZÕvill isch zÕvill

Wir gehen nun so vor, dass wir zu einem gegebenen Bruch den kleinsten Stammbruch nehmen, der noch grš§er oder gleich wie der gegebene Bruch ist. Diesen kleinsten Stammbruch finden wir, indem wir den Kehrwert des gegebenen Bruches auf die nŠchste ganze Zahl abrunden, und davon wieder den Kehrwert nehmen.

Beispiel:

Somit ist  der kleinste Stammbruch grš§er oder gleich .

Zum †berschuss nehmen wir wieder den kleinsten Stammbruch grš§er oder gleich dem †berschuss. Diesen Stammbruch zŠhlen wir ab. Und so weiter und so fort mit alternierenden Vorzeichen. Dabei hoffen wir, dass es einmal ãaufgehtÒ im Sinne, dass der †berschuss ein Stammbruch wird.

In unserem Beispiel:

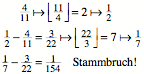
Somit haben wir eine alternierende Stammbruchzerlegung:

3.2      Formal

Es sei  der zu zerlegende Bruch. Dann arbeiten wir mit der folgenden Rekursion.

Start:

Rekursionsformel:

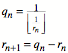
Abbruchkriterium: Wir hšren auf, sobald , also .

Wir erhalten die Stammbruchzerlegung:

Dieser Algorithmus entsteht aus dem gierigen Algorithmus durch Vertauschen der Begriffe mindestens und hšchstens. Weiter muss mit alternierendem Vorzeichen addiert werden. Der Leser oder die Leserin kann sich selber fŸr diesen Algorithmus eine Bezeichnung aus dem kulinarischen Bereich ausdenken.

3.3      Liste

 

Zerlegung in StammbrŸche

________________________

 

geordnet nach Nennern

 

Nenner = 1

1/1 = 1

 

Nenner = 2

1/2 = 1/2

2/2 = 1

 

Nenner = 3

1/3 = 1/3

2/3 = 1-1/3

3/3 = 1

 

Nenner = 4

1/4 = 1/4

2/4 = 1/2

3/4 = 1-1/4

4/4 = 1

 

Nenner = 5

1/5 = 1/5

2/5 = 1/2-1/10

3/5 = 1-1/2+1/10

4/5 = 1-1/5

5/5 = 1

 

Nenner = 6

1/6 = 1/6

2/6 = 1/3

3/6 = 1/2

4/6 = 1-1/3

5/6 = 1-1/6

6/6 = 1

 

Nenner = 7

1/7 = 1/7

2/7 = 1/3-1/21

3/7 = 1/2-1/14

4/7 = 1-1/2+1/14

5/7 = 1-1/3+1/21

6/7 = 1-1/7

7/7 = 1

 

Nenner = 8

1/8 = 1/8

2/8 = 1/4

3/8 = 1/2-1/8

4/8 = 1/2

5/8 = 1-1/2+1/8

6/8 = 1-1/4

7/8 = 1-1/8

8/8 = 1

 

Nenner = 9

1/9 = 1/9

2/9 = 1/4-1/36

3/9 = 1/3

4/9 = 1/2-1/18

5/9 = 1-1/2+1/18

6/9 = 1-1/3

7/9 = 1-1/4+1/36

8/9 = 1-1/9

9/9 = 1

 

Nenner = 10

1/10 = 1/10

2/10 = 1/5

3/10 = 1/3-1/30

4/10 = 1/2-1/10

5/10 = 1/2

6/10 = 1-1/2+1/10

7/10 = 1-1/3+1/30

8/10 = 1-1/5

9/10 = 1-1/10

10/10 = 1

 

Nenner = 11

1/11 = 1/11

2/11 = 1/5-1/55

3/11 = 1/3-1/16+1/528

4/11 = 1/2-1/7+1/154

5/11 = 1/2-1/22

6/11 = 1-1/2+1/22

7/11 = 1-1/2+1/7-1/154

8/11 = 1-1/3+1/16-1/528

9/11 = 1-1/5+1/55

10/11 = 1-1/11

11/11 = 1

 

Nenner = 12

1/12 = 1/12

2/12 = 1/6

3/12 = 1/4

4/12 = 1/3

5/12 = 1/2-1/12

6/12 = 1/2

7/12 = 1-1/2+1/12

8/12 = 1-1/3

9/12 = 1-1/4

10/12 = 1-1/6

11/12 = 1-1/12

12/12 = 1

 

Nenner = 13

1/13 = 1/13

2/13 = 1/6-1/78

3/13 = 1/4-1/52

4/13 = 1/3-1/39

5/13 = 1/2-1/8+1/104

6/13 = 1/2-1/26

7/13 = 1-1/2+1/26

8/13 = 1-1/2+1/8-1/104

9/13 = 1-1/3+1/39

10/13 = 1-1/4+1/52

11/13 = 1-1/6+1/78

12/13 = 1-1/13

13/13 = 1

 

Nenner = 14

1/14 = 1/14

2/14 = 1/7

3/14 = 1/4-1/28

4/14 = 1/3-1/21

5/14 = 1/2-1/7

6/14 = 1/2-1/14

7/14 = 1/2

8/14 = 1-1/2+1/14

9/14 = 1-1/2+1/7

10/14 = 1-1/3+1/21

11/14 = 1-1/4+1/28

12/14 = 1-1/7

13/14 = 1-1/14

14/14 = 1

 

Nenner = 15

1/15 = 1/15

2/15 = 1/7-1/105

3/15 = 1/5

4/15 = 1/3-1/15

5/15 = 1/3

6/15 = 1/2-1/10

7/15 = 1/2-1/30

8/15 = 1-1/2+1/30

9/15 = 1-1/2+1/10

10/15 = 1-1/3

11/15 = 1-1/3+1/15

12/15 = 1-1/5

13/15 = 1-1/7+1/105

14/15 = 1-1/15

15/15 = 1

 

Nenner = 16

1/16 = 1/16

2/16 = 1/8

3/16 = 1/5-1/80

4/16 = 1/4

5/16 = 1/3-1/48

6/16 = 1/2-1/8

7/16 = 1/2-1/16

8/16 = 1/2

9/16 = 1-1/2+1/16

10/16 = 1-1/2+1/8

11/16 = 1-1/3+1/48

12/16 = 1-1/4

13/16 = 1-1/5+1/80

14/16 = 1-1/8

15/16 = 1-1/16

16/16 = 1

 

Nenner = 17

1/17 = 1/17

2/17 = 1/8-1/136

3/17 = 1/5-1/42+1/3570

4/17 = 1/4-1/68

5/17 = 1/3-1/25+1/1275

6/17 = 1/2-1/6+1/51

7/17 = 1/2-1/11+1/374

8/17 = 1/2-1/34

9/17 = 1-1/2+1/34

10/17 = 1-1/2+1/11-1/374

11/17 = 1-1/2+1/6-1/51

12/17 = 1-1/3+1/25-1/1275

13/17 = 1-1/4+1/68

14/17 = 1-1/5+1/42-1/3570

15/17 = 1-1/8+1/136

16/17 = 1-1/17

17/17 = 1

 

Nenner = 18

1/18 = 1/18

2/18 = 1/9

3/18 = 1/6

4/18 = 1/4-1/36

5/18 = 1/3-1/18

6/18 = 1/3

7/18 = 1/2-1/9

8/18 = 1/2-1/18

9/18 = 1/2

10/18 = 1-1/2+1/18

11/18 = 1-1/2+1/9

12/18 = 1-1/3

13/18 = 1-1/3+1/18

14/18 = 1-1/4+1/36

15/18 = 1-1/6

16/18 = 1-1/9

17/18 = 1-1/18

18/18 = 1

 

Nenner = 19

1/19 = 1/19

2/19 = 1/9-1/171

3/19 = 1/6-1/114

4/19 = 1/4-1/25+1/1900

5/19 = 1/3-1/14+1/798

6/19 = 1/3-1/57

7/19 = 1/2-1/7+1/88-1/11704

8/19 = 1/2-1/12+1/228

9/19 = 1/2-1/38

10/19 = 1-1/2+1/38

11/19 = 1-1/2+1/12-1/228

12/19 = 1-1/2+1/7-1/88+1/11704

13/19 = 1-1/3+1/57

14/19 = 1-1/3+1/14-1/798

15/19 = 1-1/4+1/25-1/1900

16/19 = 1-1/6+1/114

17/19 = 1-1/9+1/171

18/19 = 1-1/19

19/19 = 1

 

Nenner = 20

1/20 = 1/20

2/20 = 1/10

3/20 = 1/6-1/60

4/20 = 1/5

5/20 = 1/4

6/20 = 1/3-1/30

7/20 = 1/2-1/6+1/60

8/20 = 1/2-1/10

9/20 = 1/2-1/20

10/20 = 1/2

11/20 = 1-1/2+1/20

12/20 = 1-1/2+1/10

13/20 = 1-1/2+1/6-1/60

14/20 = 1-1/3+1/30

15/20 = 1-1/4

16/20 = 1-1/5

17/20 = 1-1/6+1/60

18/20 = 1-1/10

19/20 = 1-1/20

20/20 = 1

 

3.4      Die Formel von Leibniz

Sie lautet:

Da haben wir alternierendes Vorzeichen.

Wir setzen nun den ãBruchÒ in den alternierenden Algorithmus ein:

 

Stammbrueche(float(PI),4);

 

3.141592654/4 =
1-1/4+1/28-1/3163+1/30091756-1/1611843016646488+1/59510565713866219235349062746112

 

Da  irrational ist, haben wir wie beim Basler Problem ein unsinniges Beispiel.

4        Vergleich der beiden Verfahren

4.1      Nenner 19

Wir vergleichen exemplarisch die Resultate bei BrŸchen mit dem Nenner 19.

Der gierige Algorithmus liefert:

 

Nenner = 19

1/19 = 1/19

2/19 = 1/10+1/190

3/19 = 1/7+1/67+1/8911

4/19 = 1/5+1/95

5/19 = 1/4+1/76

6/19 = 1/4+1/16+1/304

7/19 = 1/3+1/29+1/1653

8/19 = 1/3+1/12+1/228

9/19 = 1/3+1/8+1/66+1/5016

10/19 = 1/2+1/38

11/19 = 1/2+1/13+1/494

12/19 = 1/2+1/8+1/152

13/19 = 1/2+1/6+1/57

14/19 = 1/2+1/5+1/28+1/887+1/2359420

15/19 = 1/2+1/4+1/26+1/988

16/19 = 1/2+1/3+1/114

17/19 = 1/2+1/3+1/17+1/388+1/375972

18/19 = 1/2+1/3+1/9+1/342

19/19 = 1

 

Der alternierende Algorithmus liefert:

 

Nenner = 19

1/19 = 1/19

2/19 = 1/9-1/171

3/19 = 1/6-1/114

4/19 = 1/4-1/25+1/1900

5/19 = 1/3-1/14+1/798

6/19 = 1/3-1/57

7/19 = 1/2-1/7+1/88-1/11704

8/19 = 1/2-1/12+1/228

9/19 = 1/2-1/38

10/19 = 1-1/2+1/38

11/19 = 1-1/2+1/12-1/228

12/19 = 1-1/2+1/7-1/88+1/11704

13/19 = 1-1/3+1/57

14/19 = 1-1/3+1/14-1/798

15/19 = 1-1/4+1/25-1/1900

16/19 = 1-1/6+1/114

17/19 = 1-1/9+1/171

18/19 = 1-1/19

19/19 = 1

 

Wir sehen unterschiedliche Profile. Die Maximalzahl der benštigten StammbrŸche ist bei beiden Verfahren 5.

4.2      Maximale Anzahl

Im folgenden Diagramm wird zu gegebenem Nenner die maximale Anzahl der benštigten StammbrŸche dargestellt, fŸr den gierigen Algorithmus in rot, fŸr den alternierenden Algorithmus in blau, seitlich etwas versetzt. Die Nenner laufen von 1 bis 20.

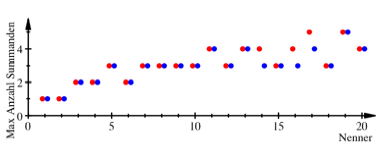
Maximalzahlen der benštigten StammbrŸche

Wir sehen, dass die beiden Verfahren fast immer zur selben Maximalzahl fŸhren, Ausnahmen sind die Nenner 14, 16 und 17, in denen der alternierende Algorithmus besser ist.


Im Gro§versuch sehen wir, dass allerdings der gierige Algorithmus auch besser sein kann.

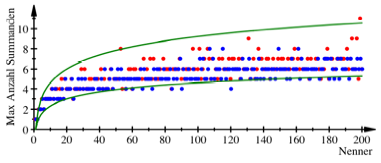
Gro§versuch