Hans Walser, [20110125b]

Steigung und Richtung

Anregung: M. B., Z. und H. F., B.

1 Worum es geht

Die Begriffe Steigung und Richtung werden oft verwechselt. Als Folge wird dann auch die Krümmung falsch zugeordnet.

2 Steigung

2.1 Konstante Steigung

Bei der Geraden ist alles einfach. Die Steigung ist konstant.

Konstante Steigung bei der Geraden

2.2 Gleichmäßige Zunahme der Steigung: Parabel

Nun lassen wir die Steigung gleichmäßig wachsen. Dies können wir am rechten Rand der Steigungsdreiecke gut einsehen. Die Dreiecke werden aufgestockt.

Es wird immer steiler

Wir erhalten eine Parabel.

Parabel

Im folgenden Bild ist nur die Änderung (Zunahme) der Steigung eingezeichnet.

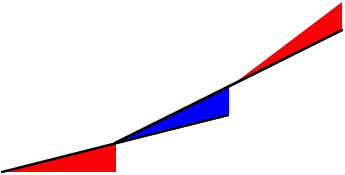
Konstante Änderung der Steigung

Das gibt natürlich dieselbe Parabel.

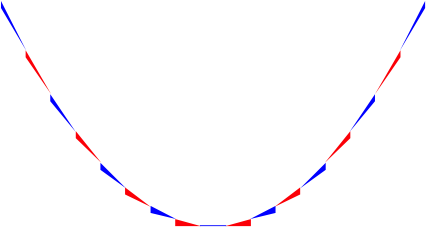
Parabel

2.3 Gleichmäßige Zunahme der Änderung der Steigung

Nun soll aber bereits die Änderung der Steigung zunehmen.

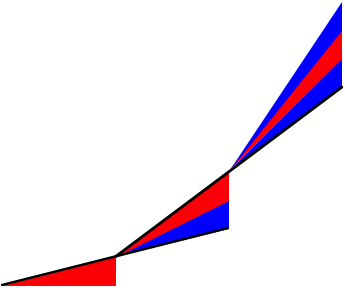
Wachsende Zunahme der Steigung

Das Zeug wächst recht schnell und erinnert an eine kubische Parabel.

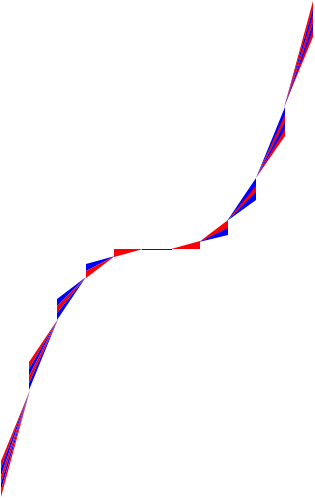
Kubische Parabel

3 Richtung

3.1 Konstanter Richtung

Bei der Geraden ist alles einfach. Die Richtung ist konstant.

Konstante Richtung bei der Geraden

3.2 Gleichmäßige Zunahme der Richtung: Kreis

Nun wird der Winkel gleichmäßig größer. Die Richtung wird immer um gleich viel verändert. Die Sektoren werden verdreht aufgesetzt.

Der Winkel wächst gleichmäßig

Auf diese Weise erhalten wir einen Kreis (genau genommen ein gleichseitig gleichwinkliges Polygon).

Kreis

Im folgenden Bild ist nur die Änderung (Zunahme) der Richtung eingezeichnet.

Konstante Änderung der Richtung

Das gibt natürlich denselben Kreis.

Kreis

3.3 Gleichmäßige Zunahme der Änderung der Richtung

Nun soll aber bereits die Änderung der Richtung zunehmen.

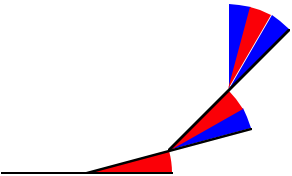
Wachsende Zunahme der Richtung

Das führt zu einer immer stärker gekrümmten Kurve. Die Kurve heißt Klothoide.

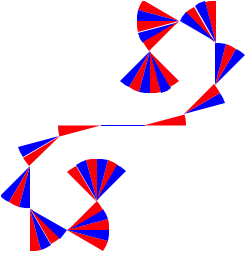
Klothoide

Die folgende Abbildung zeigt eine kontinuierliche Klothoide. Sie wickelt sich an beiden Enden ein.

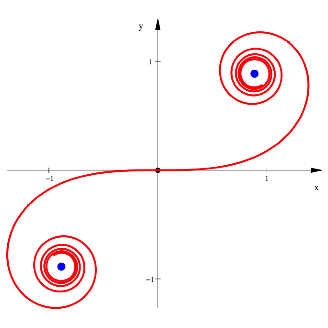
Klothoide