Hans Walser, [20180622]

Steigung und Steigungswinkel

Anregung: M. H., V.

1     Worum es geht

SchŸlerinnen und SchŸle verwechseln gelegentlich die Begriffe Steigung und Steigungswinkel.

Gibt es ein Beispiel, wo die Ma§zahlen der Steigung in % und der Steigungswinkel in ¡ Ÿbereinstimmen?

2     Prozent und Grad

Leider gibt es au§er der trivialen Lšsung  keine weitere Lšsung.

3     Prozent und Minuten

Wenn wir den Steigungswinkel a nicht in ¡, sondern in Minuten angeben, haben wir eine Lšsung. Aus

 

                                                                                           (1)

 

 

ergibt sich:

 

                         (2)

 

 

4     Weitere Beispiele

Es geht auch mit anderen Ma§einheiten.

4.1    Prozent und Sekunden

Es ist:

 

                                                                                             (3)

 

 

4.2    Promille und Minuten

Es ist:

 

                                               ä                                          (4)

 

 

4.3    Promille und Sekunden

Es ist:

 

                                                ä                                           (5)

 

 

5     Hintergrund

5.1    Problemstellung

Wir arbeiten mit einem Winkelma§, welches den Vollkreis in N Teile unterteilt. FŸr das ¡-Ma§ ist dann N = 360.

Weiter soll die Steigung in % angegeben werden.

Wir nehmen weiter an, dass die Tangensfunktion im Bogenma§ operiert.

Damit suchen wir Lšsungen fŸr t der Gleichung:

 

                                                                                                                (6)

 

 

Die triviale Lšsung ist t = 0.

Die Gleichung (6) formen wir um:

 

                                                                                                              (7)

 

 

5.2    Grafische Lšsung

Wir vergleichen die Funktionsgrafen der beiden Funktionen:

 

                                             (rote Kurve)                                       (8)

 

 

                                                      (blaue Kurve)                                                (9)

 

 

Gesucht sind die Schnittpunkte der beiden Kurven.

5.2.1   N = 360

FŸr N = 360, also das ¡-Ma§, ergeben sich die beiden Kurven der Abbildung 1.

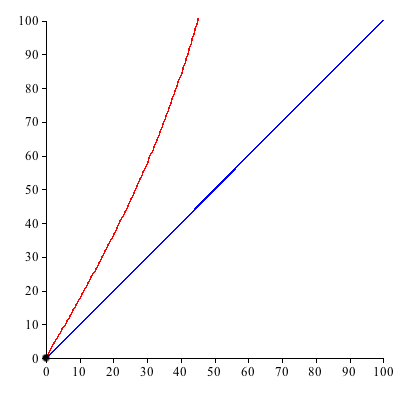
Abb. 1: Situation im ¡-Ma§

Wir haben nur den trivialen Schnittpunkt (0, 0).

5.2.2   N = 1000

FŸr N = 1000 ergeben sich die beiden Kurven der Abbildung 2.

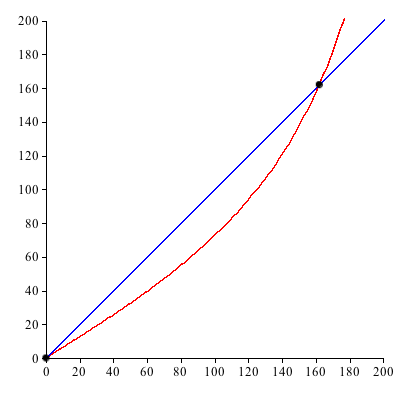
Abb. 2: N = 1000

Neben dem trivialen Schnittpunkt haben wir den Schnittpunkt (161.97, 161.97). Der Schnittpunkt wurde mit dem Verfahren von Newton-Raphson numerisch ermittelt.

5.3    Wo ist die Grenze?

Der Vergleich der beiden Beispiele N = 360 und N = 1000 legt nahe, dass es dazwischen eine Grenze gibt, so dass es fŸr kleinere N nur die triviale Lšsung, fŸr grš§ere N aber auch eine nichttriviale Lšsung gibt.

Im Grenzfall hat die Funktion f im Ursprung die Steigung 1. Aus (8) ergibt sich:

 

                                                                                                     (10)

 

 

Die Bedingung

 

                                                                                                                       (11)

 

 

fŸhrt auf:

 

                                                                                                         (12)

 

 

FŸr das ¡-Ma§ ist N = 360 und damit unterhalb dieser Grenze.

Wenn wir in Minuten rechnen, ist  und damit oberhalb dieser Grenze. Analog fŸr Sekunden.

Wenn wir mit Promillen arbeiten, ist in (6), (7), (8) sowie (10) und (12) der Faktor 100 durch 1000 zu ersetzen. Die kritische Grenze ist dann .

 

Last modified 2018-06-23