Hans Walser, [20161110]
SteigungsfŠcher
Anregung: Heinz Klaus Strick, Leverkusen
1 Worum geht es
Grafische Methode zur Bestimmung der Anzahl der Teiler einer natŸrlichen Zahl.
2 Basisfigur
Wir zeichnen in einem kartesischen Koordinatensystem vom Punkt (–1, 0) aus die Strahlen mit den Steigungen 0, 1, 2, 3, 4, ... (Abb. 1 fŸr die Steigungen 1, ... , 12). So erhalten wir den SteigungsfŠcher.
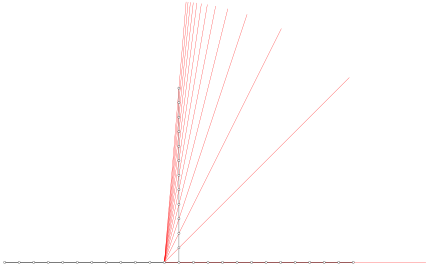
Abb. 1: SteigungsfŠcher
3 Kopien des SteigungsfŠchers
Wir setzen Kopien des SteigungsfŠchers an den Punkten (–2, 0), (–3, 0), ... an (Abb. 2).
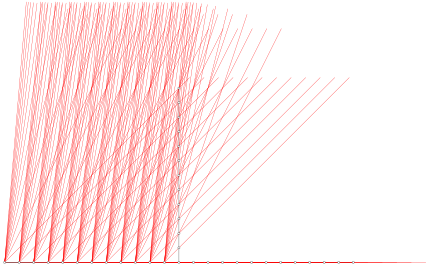
Abb. 2: Mehr SteigungsfŠcher
Die ganzzahligen Punkte auf der y-Achse werden von mindestens einem Strahl eines FŠchers getroffen.
4 Anzahl der Teiler. Primzahlen
Die Anzahl der Strahle durch den Punkt (0, n) ist die Anzahl der Teiler von n.
FŸr n = 0 haben wir unendliche viele Teiler, fŸr n = 1 genau einen Teiler, fŸr die Primzahlen genau zwei Teiler, fŸr die Ÿbrigen Zahlen mehr als zwei Teiler. Das Verfahren funktioniert also auch als ãSieb des EratosthenesÒ fŸr die Primzahlen.