Hans Walser, [20230717]
Steile Gerade
Idee und Anregung: Peter Gallin, Zürich
1 Worum es geht
Ein Optimierungsproblem führt zum Goldenen Schnitt.
2 Die Kinematik
Die Abbildung 1 gibt einen Mechanismus mit zwei ähnlichen Rechtecken, einem Viertelkreis und einer Geraden, welche durch je eine obere Ecke der Rechtecke verläuft.
Abb. 1: Kinematik
Die rote Gerade ist zunächst waagrecht, wird dann immer steiler, aber dann nimmt die Steigung wieder ab und am Schluss ist sie wieder waagrecht. In welcher Position ist die Gerade am steilsten?
3 Bearbeitung
Wir arbeiten mit den Bezeichnungen der Abbildung 2.
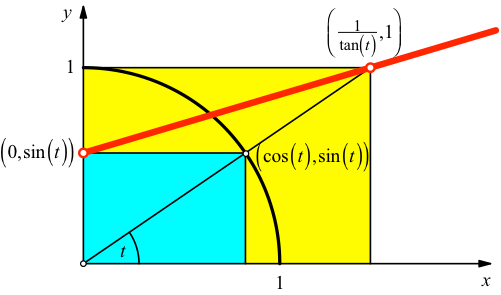
Abb. 2: Bezeichnungen
Für die Steigung m(t) der roten Geraden lesen wir ab:
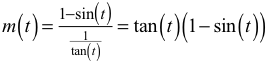
Die Optimierungsbedingung
![]()
führt auf die Gleichung:
Diese kubische Gleichung hat für sin(t) die drei Lösungen sin(t1) = 1, sin(t2) = 1/Φ, sin(t3) = – Φ. Die für uns relevante Lösung ist sin(t2) = 1/Φ. Dabei ist Φ der Goldene Schnitt, Φ ≈ 1.618.
Das zur steilsten roten Geraden gehörende t ist also t = arcsin(1/ Φ) ≈ 0.6662, also etwa 38.173°. (Beachte: das ist nicht der Steigungswinkel der roten Geraden, sondern der Steigungswinkel der gemeinsamen Diagonalen der beiden Rechtecke. )
Die zugehörige maximale Steigung der roten Geraden ist m ≈ 0.3003. Die Abbildung 3 zeigt die zugehörige Gerade. Der Steigungswinkel ist etwa 16.714°.
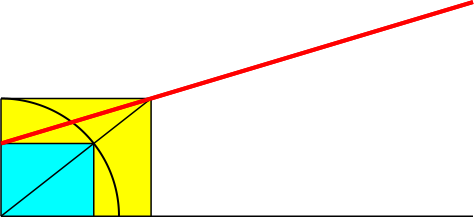
Abb. 3: Steilste Gerade
In der optimalen Variante (Abb. 3) haben die beiden Rechtecke ein Seitenverhältnis 1:√Φ ≈ 1:1.272. Wieder einmal die Wurzel aus dem Goldenen Schnitt.